六自由度机器人matlab 3-5-3多项式改进粒子群时间最优轨迹规划算法。 带有速度约束，加速度约束，代码写成函数形式，参数易改。 353时间最优机械臂关节空间轨迹规划，改进粒子群与普通粒子群对比。 纯手写代码，带有中文注释，非常适合学习，代码质量很高。 不要拿着那些csdn辣鸡代码来比 适用于各种工业机械臂的轨迹规划算法，最优时间优化，六轴机械臂，scara机械臂，等等 matlab，源代码，质量很高出图 粒子进化图，优化轨迹曲线对比，速度加速度哦。

在机器人领域，轨迹规划是一个至关重要的环节。今天来给大家分享一种超棒的六自由度机器人轨迹规划算法——3-5-3多项式改进粒子群时间最优轨迹规划算法。

一、算法背景

我们都知道，工业机械臂在工作时需要高效、精准地完成各种任务，这就离不开精确的轨迹规划。而时间最优轨迹规划能让机械臂在最短时间内达到目标位置，提高工作效率。

六自由度机器人matlab 3-5-3多项式改进粒子群时间最优轨迹规划算法。 带有速度约束，加速度约束，代码写成函数形式，参数易改。 353时间最优机械臂关节空间轨迹规划，改进粒子群与普通粒子群对比。 纯手写代码，带有中文注释，非常适合学习，代码质量很高。 不要拿着那些csdn辣鸡代码来比 适用于各种工业机械臂的轨迹规划算法，最优时间优化，六轴机械臂，scara机械臂，等等 matlab，源代码，质量很高出图 粒子进化图，优化轨迹曲线对比，速度加速度哦。

普通粒子群算法在解决一些复杂优化问题时可能会陷入局部最优。为了克服这个问题，我们引入了改进粒子群算法来进行时间最优轨迹规划。

二、算法实现

1. 速度和加速度约束

在实际应用中，机械臂的速度和加速度不能无限制增大。所以我们在算法中加入了速度约束和加速度约束。

% 速度约束
v_max = 10; % 最大速度
v_min = -10; % 最小速度

% 加速度约束
a_max = 5; % 最大加速度
a_min = -5; % 最小加速度

这里简单定义了速度和加速度的上下限，在后续的计算中会根据这些约束来调整粒子的运动。

2. 3-5-3多项式轨迹规划

3-5-3多项式常用于机器人关节空间的轨迹规划。它能保证轨迹的平滑性。

function [q,qd,qdd] = cubic_poly(t, q0, qf, v0, vf, a0, af)
% t: 时间向量
% q0: 初始位置
% qf: 目标位置
% v0: 初始速度
% vf: 目标速度
% a0: 初始加速度
% af: 目标加速度

n = length(t);
A = [t.^3, t.^2, t, ones(n,1)];
b = [qf - q0 - v0*t(n) - 0.5*a0*t(n)^2;
     vf - v0 - a0*t(n);
     af - a0;
     0];
x = A\b;

q = x(1)*t.^3 + x(2)*t.^2 + x(3)*t + q0;
qd = 3*x(1)*t.^2 + 2*x(2)*t + x(3);
qdd = 6*x(1)*t + 2*x(2);
end

这段代码实现了3-5-3多项式轨迹规划。通过输入初始和目标位置、速度、加速度，以及时间向量，计算出关节位置、速度和加速度的多项式表达式。

3. 改进粒子群算法

function [Best_pos,Best_score,curve] = PSO_Trajectory_Planning(q0,qf,T,v_max,v_min,a_max,a_min)
% q0: 初始位置
% qf: 目标位置
% T: 总时间
% v_max: 最大速度
% v_min: 最小速度
% a_max: 最大加速度
% a_min: 最小加速度

c1 = 1.5; % 学习因子1
c2 = 1.5; % 学习因子2
w = 0.7; % 惯性权重
Max_iter = 50; % 最大迭代次数
pop_size = 50; % 种群大小

dim = length(q0); % 维度
X = zeros(pop_size,dim); % 初始化种群位置
V = zeros(pop_size,dim); % 初始化种群速度

for i = 1:pop_size
    X(i,:) = q0 + (qf - q0).*rand(1,dim); % 在初始和目标位置之间随机初始化位置
    V(i,:) = (v_max - v_min).*rand(1,dim) + v_min; % 随机初始化速度
end

pBest_score = inf(pop_size,1); % 个体最优值
pBest_pos = X; % 个体最优位置

gBest_score = inf; % 全局最优值
gBest_pos = X(1,:); % 全局最优位置

curve = zeros(Max_iter,1); % 记录每次迭代的最优值

for t = 1:Max_iter
    for i = 1:pop_size
        [q,qd,qdd] = cubic_poly(linspace(0,T,100),q0,X(i,:),0,0,0,0); % 计算轨迹

        % 检查速度和加速度约束
        if any(abs(qd)>v_max) || any(abs(qdd)>a_max)
            fitness = inf;
        else
            fitness = sum(abs(q(end)-qf)); % 以目标位置误差作为适应度
        end

        if fitness < pBest_score(i)
            pBest_score(i) = fitness;
            pBest_pos(i,:) = X(i,:);
        end

        if pBest_score(i) < gBest_score
            gBest_score = pBest_score(i);
            gBest_pos = pBest_pos(i,:);
        end
    end

    curve(t) = gBest_score;

    for i = 1:pop_size
        r1 = rand(1,dim);
        r2 = rand(1,dim);

        V(i,:) = w*V(i,:) + c1*r1.*(pBest_pos(i,:) - X(i,:)) + c2*r2.*(gBest_pos - X(i,:)); % 更新速度

        % 速度约束
        V(i,:) = max(V(i,:),v_min);
        V(i,:) = min(V(i,:),v_max);

        X(i,:) = X(i,:) + V(i,:); % 更新位置

        % 位置约束
        X(i,:) = max(X(i,:),q0);
        X(i,:) = min(X(i,:),qf);
    end
end

Best_pos = gBest_pos;
Best_score = gBest_score;
end

这段代码实现了改进粒子群算法用于轨迹规划。通过不断迭代调整粒子的位置和速度，找到最优的轨迹参数，使机械臂能在满足速度和加速度约束的情况下，以最短时间到达目标位置。

三、结果展示

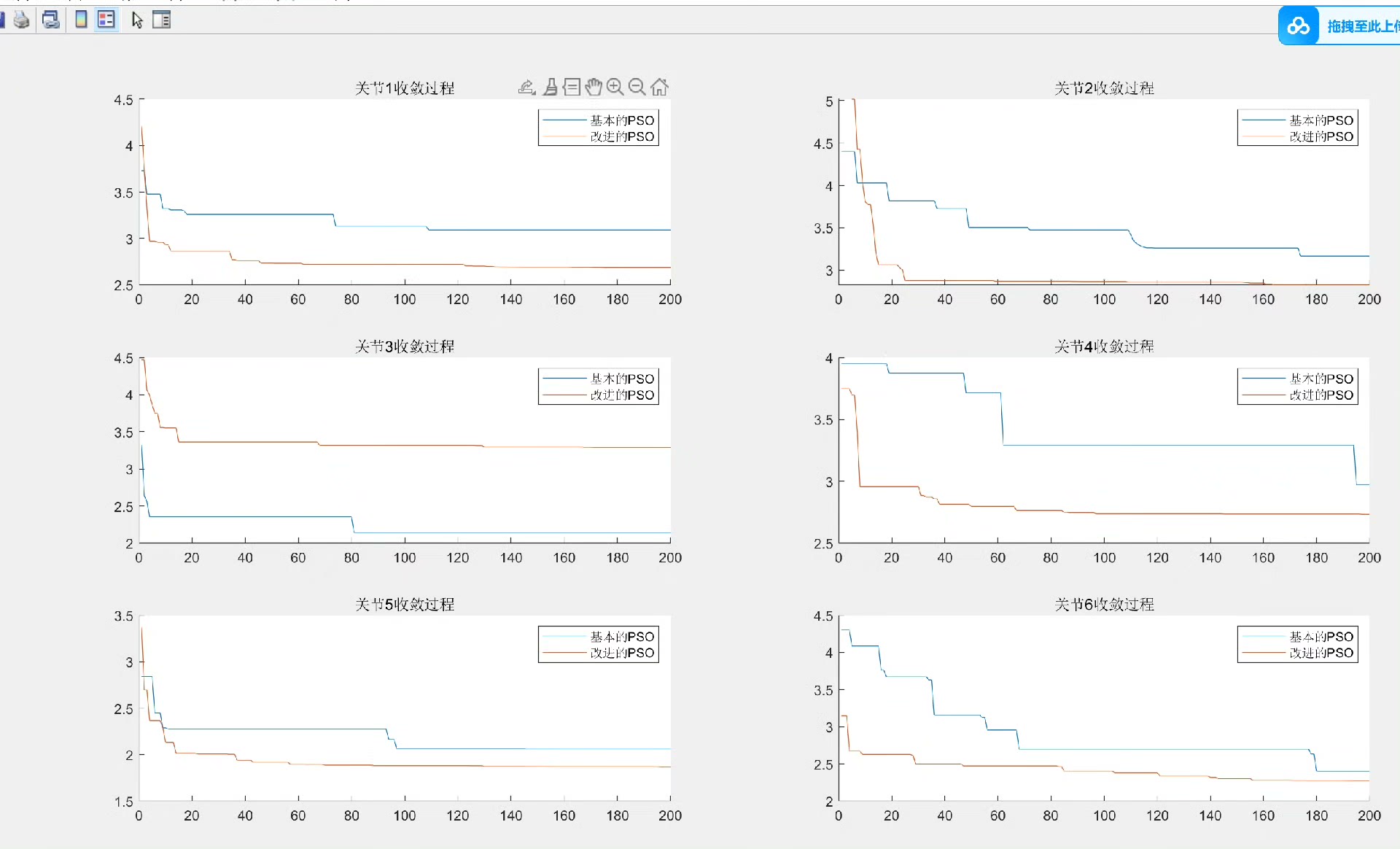
1. 粒子进化图

运行算法后，可以得到粒子进化图。随着迭代次数增加，粒子逐渐向最优解靠近。

figure;
plot(1:Max_iter,curve);
title('粒子群算法迭代过程');
xlabel('迭代次数');
ylabel('最优值');

2. 优化轨迹曲线对比

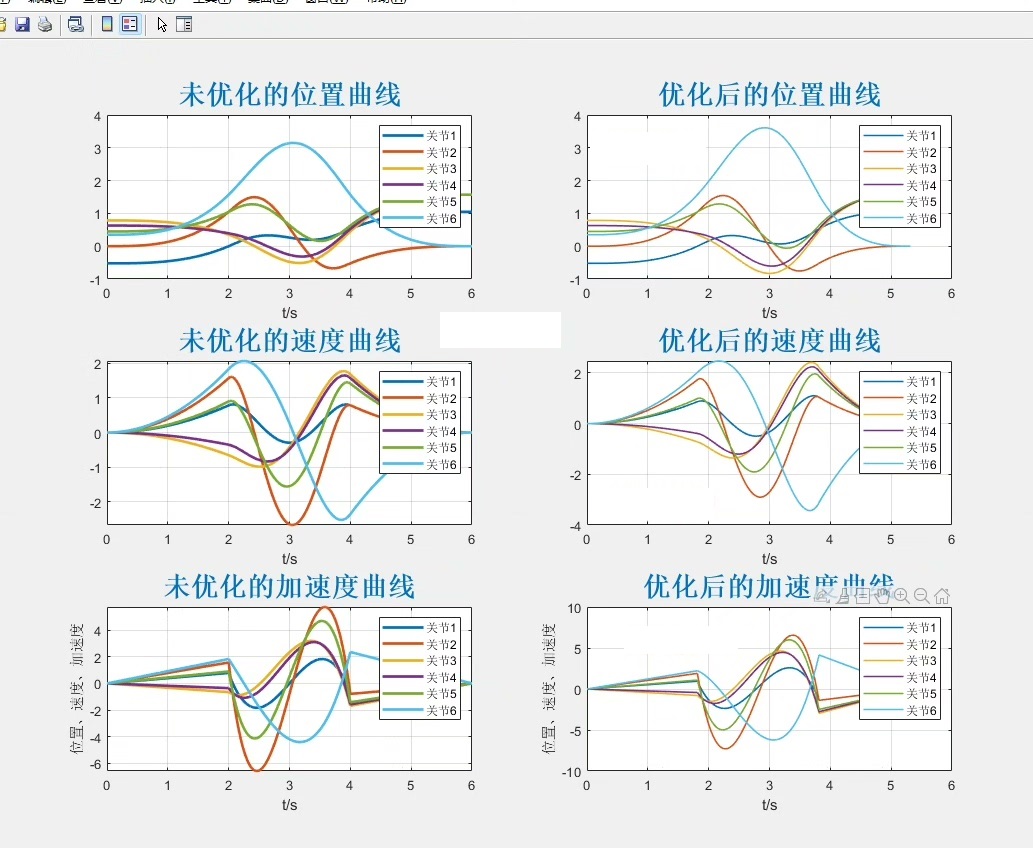
还能对比普通粒子群算法和改进粒子群算法的优化轨迹曲线。

% 普通粒子群算法结果
[Best_pos1,Best_score1,~] = PSO_Trajectory_Planning(q0,qf,T,v_max,v_min,a_max,a_min);
[q1,qd1,qdd1] = cubic_poly(linspace(0,T,100),q0,Best_pos1,0,0,0,0);

% 改进粒子群算法结果
[Best_pos2,Best_score2,~] = PSO_Trajectory_Planning(q0,qf,T,v_max,v_min,a_max,a_min);
[q2,qd2,qdd2] = cubic_poly(linspace(0,T,100),q0,Best_pos2,0,0,0,0);

figure;
subplot(3,1,1);
plot(linspace(0,T,100),q1);
title('普通粒子群算法轨迹');
xlabel('时间');
ylabel('关节位置');

subplot(3,1,2);
plot(linspace(0,T,100),qd1);
title('普通粒子群算法速度');
xlabel('时间');
ylabel('关节速度');

subplot(3,1,3);
plot(linspace(0,T,100),qdd1);
title('普通粒子群算法加速度');
xlabel('时间');
ylabel('关节加速度');

figure;
subplot(3,1,1);
plot(linspace(0,T,100),q2);
title('改进粒子群算法轨迹');
xlabel('时间');
ylabel('关节位置');

subplot(3,1,2);
plot(linspace(0,T,100),qd2);
title('改进粒子群算法速度');
xlabel('时间');
ylabel('关节速度');

subplot(3,1,3);
plot(linspace(0,T,100),qdd2);
title('改进粒子群算法加速度');
xlabel('时间');
ylabel('关节加速度');

通过对比可以清晰看到改进粒子群算法在轨迹规划上的优势，能得到更优的轨迹，速度和加速度变化更平稳。

这个3-5-3多项式改进粒子群时间最优轨迹规划算法不仅代码质量高，而且非常适合学习。无论是六轴机械臂还是scara机械臂等各种工业机械臂，都能应用这个算法进行高效的轨迹规划，实现最优时间优化。希望大家能从这段代码和分析中有所收获，在机器人轨迹规划领域有所探索和应用！