IMU与GPS融合定位，扩展卡尔曼滤波，cpp实现，机器人状态估计，有注释和运行说明

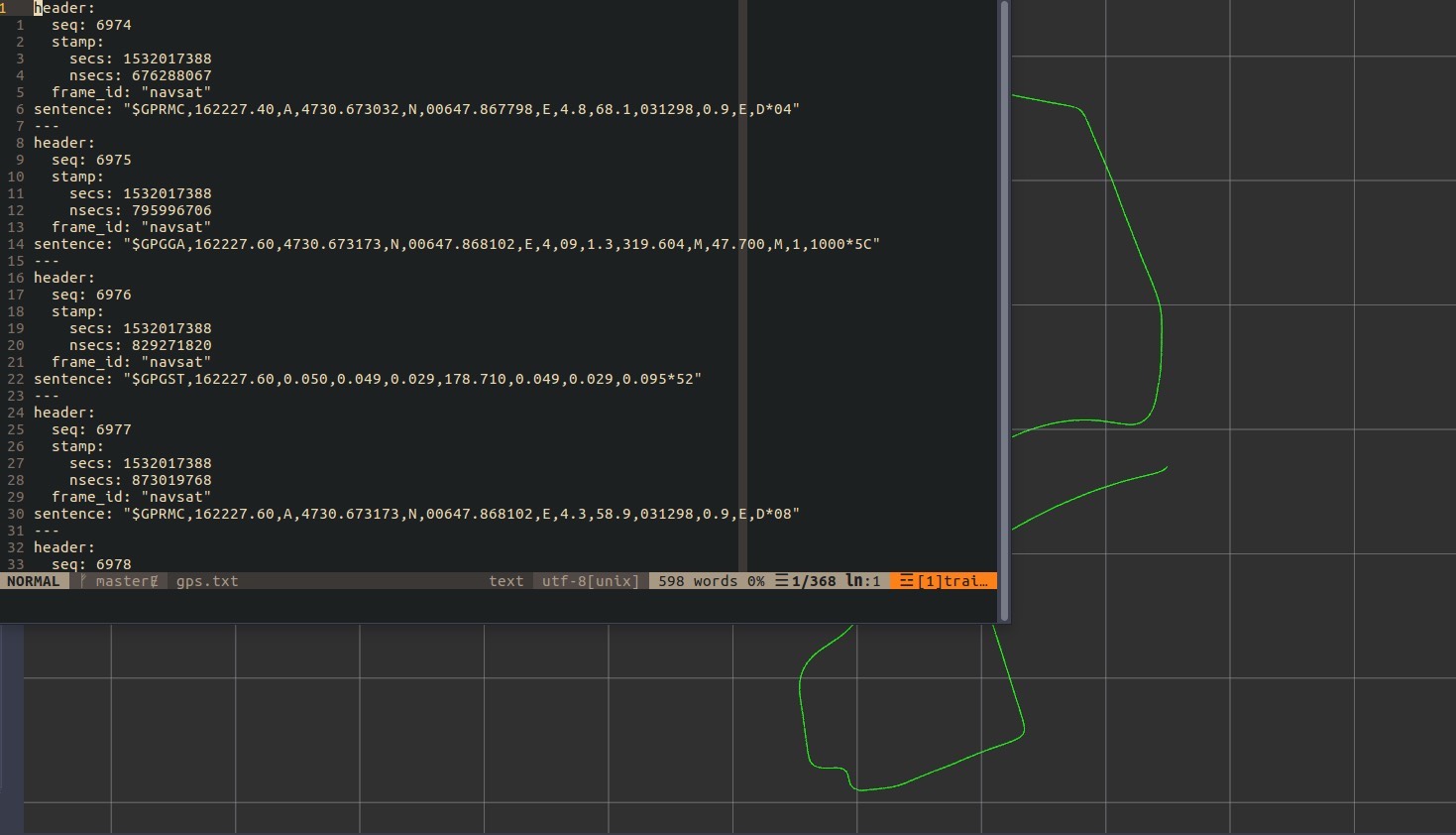
在机器人状态估计领域，IMU（惯性测量单元）和 GPS（全球定位系统）的融合定位是一项关键技术。IMU 能够高频输出机器人的加速度和角速度信息，但随着时间推移会产生累计误差；GPS 则能提供绝对位置信息，精度较高但更新频率较低。通过将两者融合，可以获得更准确、稳定的机器人状态估计。扩展卡尔曼滤波（EKF）是一种常用的融合算法，本文将介绍如何使用 C++ 实现基于 EKF 的 IMU 与 GPS 融合定位，并附上详细注释和运行说明。

原理简介

扩展卡尔曼滤波是卡尔曼滤波在非线性系统中的扩展。在机器人定位场景中，系统状态方程和观测方程通常是非线性的。

• 系统状态方程：一般可表示为 $x{k} = f(x{k - 1}, u{k - 1}) + w{k - 1}$，其中 $x{k}$ 是 $k$ 时刻的系统状态（包含位置、速度、姿态等），$f$ 是非线性函数，$u{k - 1}$ 是 $k - 1$ 时刻的控制输入（如 IMU 测量的加速度和角速度），$w_{k - 1}$ 是过程噪声。

• 观测方程：$z{k} = h(x{k}) + v{k}$，$z{k}$ 是 $k$ 时刻的观测值（如 GPS 测量的位置），$h$ 是非线性观测函数，$v_{k}$ 是观测噪声。

EKF 的核心步骤包括预测和更新：

1. 预测：根据上一时刻的状态估计和控制输入，预测当前时刻的状态和协方差。
2. 更新：利用当前时刻的观测值，对预测的状态进行修正，得到更准确的估计。

C++ 代码实现

#include <iostream>
#include <Eigen/Dense>
// Eigen 库用于矩阵运算

// 定义状态向量维度
const int STATE_DIM = 6;  
// 位置 (x, y, z)，速度 (vx, vy, vz)

// 定义观测向量维度
const int OBS_DIM = 3;    
// GPS 测量的位置 (x, y, z)

// 定义过程噪声协方差
Eigen::MatrixXd Q(STATE_DIM, STATE_DIM);  

// 定义观测噪声协方差
Eigen::MatrixXd R(OBS_DIM, OBS_DIM);  

// 状态向量
Eigen::VectorXd x_hat(STATE_DIM);  
// 状态估计协方差
Eigen::MatrixXd P(STATE_DIM, STATE_DIM);  

// 预测函数
void predict(const Eigen::VectorXd& u, double dt) {
    // 状态转移矩阵 F
    Eigen::MatrixXd F = Eigen::MatrixXd::Identity(STATE_DIM, STATE_DIM);
    F.block<3, 3>(0, 3) = Eigen::MatrixXd::Identity(3, 3) * dt;

    // 非线性状态转移函数 f
    x_hat.block<3, 1>(0, 0) += x_hat.block<3, 1>(3, 0) * dt;
    x_hat.block<3, 1>(3, 0) += u.block<3, 1>(0, 0) * dt;

    // 过程噪声驱动矩阵 G
    Eigen::MatrixXd G(STATE_DIM, STATE_DIM);
    G.block<3, 3>(3, 0) = Eigen::MatrixXd::Identity(3, 3) * dt;

    // 更新状态估计协方差 P
    P = F * P * F.transpose() + G * Q * G.transpose();
}

// 更新函数
void update(const Eigen::VectorXd& z) {
    // 观测矩阵 H
    Eigen::MatrixXd H = Eigen::MatrixXd::Zero(OBS_DIM, STATE_DIM);
    H.block<3, 3>(0, 0) = Eigen::MatrixXd::Identity(3, 3);

    // 卡尔曼增益 K
    Eigen::MatrixXd S = H * P * H.transpose() + R;
    Eigen::MatrixXd K = P * H.transpose() * S.inverse();

    // 更新状态估计 x_hat
    x_hat = x_hat + K * (z - H * x_hat);

    // 更新状态估计协方差 P
    P = (Eigen::MatrixXd::Identity(STATE_DIM, STATE_DIM) - K * H) * P;
}

代码分析

1. 头文件和初始化：引入 Eigen 库用于高效的矩阵运算。定义了状态向量和观测向量的维度，以及过程噪声协方差 Q、观测噪声协方差 R、状态向量 x_hat 和状态估计协方差 P。
2. 预测函数 predict：
   - 首先构建状态转移矩阵 F，它描述了状态如何随时间变化。位置的更新依赖于速度，速度的更新依赖于加速度（控制输入 u）。
   - 通过非线性状态转移函数 f 更新状态向量 x_hat。
   - 构建过程噪声驱动矩阵 G，用于计算过程噪声对状态估计协方差 P 的影响。
   - 最后根据公式更新状态估计协方差 P。
3. 更新函数 update：
   - 构建观测矩阵 H，它将状态向量映射到观测空间。在我们的例子中，GPS 直接观测位置，所以 H 的前 3 行 3 列是单位矩阵。
   - 计算卡尔曼增益 K，它决定了观测值对状态估计的修正程度。
   - 根据观测值 z 更新状态估计 x_hat。
   - 最后更新状态估计协方差 P，使估计更加准确。

运行说明

1. 初始化参数：在实际使用前，需要初始化过程噪声协方差 Q、观测噪声协方差 R、初始状态向量 x_hat 和初始状态估计协方差 P。例如：

Q.setIdentity();
Q = Q * 0.001;

R.setIdentity();
R = R * 0.1;

x_hat.setZero();
P.setIdentity();

这里将 Q 设置为较小的值，表示过程噪声较小；R 设置为相对较大的值，表示 GPS 观测噪声相对较大。初始状态向量设为零，初始协方差设为单位矩阵。

1. 输入数据：准备好 IMU 测量的加速度和角速度数据（作为控制输入 u）以及 GPS 测量的位置数据（作为观测值 z）。数据的时间间隔 dt 需根据实际测量频率确定。

1. 调用函数：在主程序中，按照时间顺序依次调用 predict 函数和 update 函数。例如：

// 假设已经获取到 IMU 数据 u 和 GPS 数据 z，以及时间间隔 dt
predict(u, dt);
update(z);

// 输出更新后的状态估计
std::cout << "Estimated state: " << x_hat.transpose() << std::endl;

通过上述步骤，就可以实现基于扩展卡尔曼滤波的 IMU 与 GPS 融合定位，为机器人提供更准确的状态估计。希望这篇文章对您在机器人定位领域的研究和实践有所帮助。

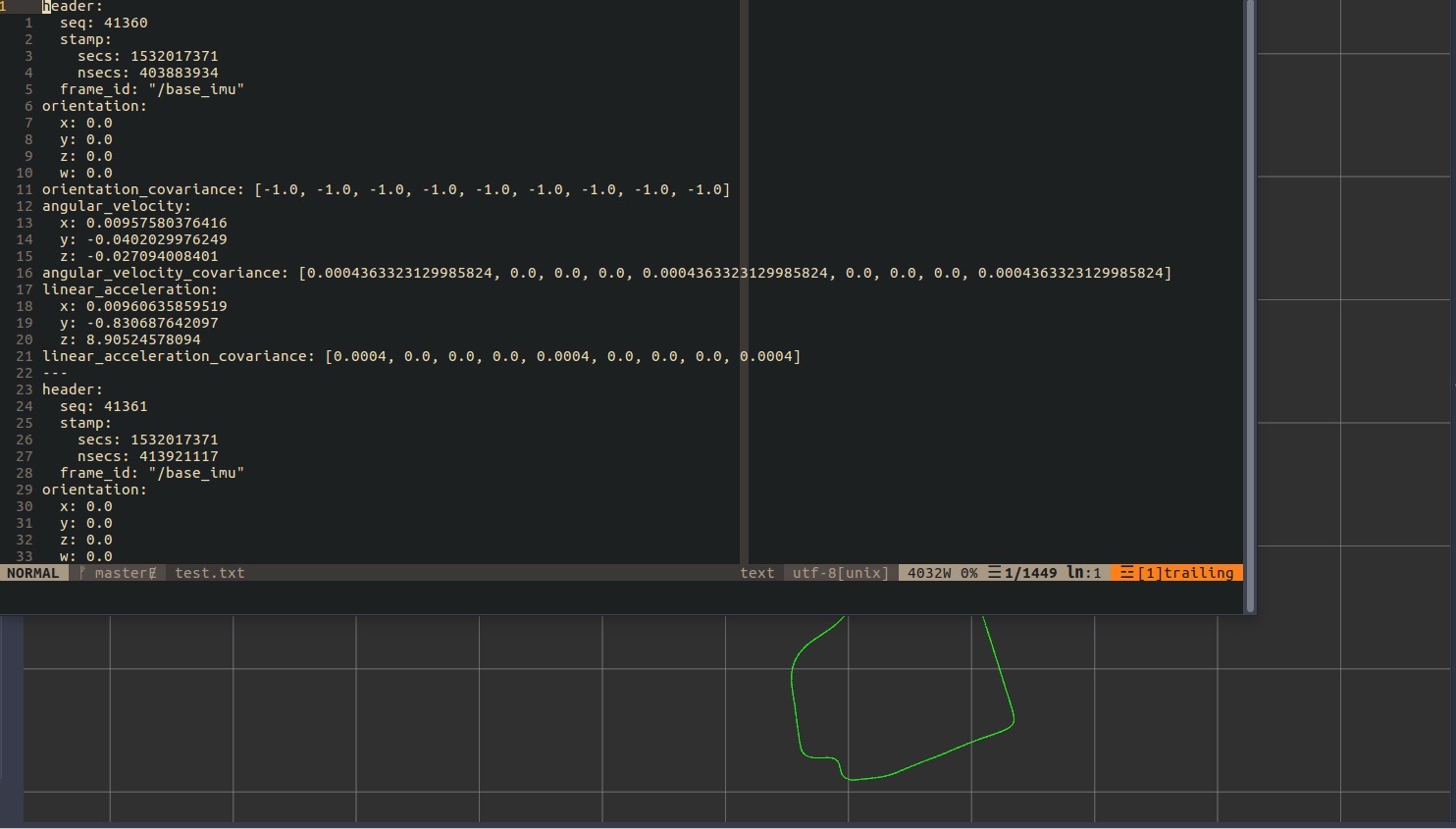
IMU与GPS融合定位，扩展卡尔曼滤波，cpp实现，机器人状态估计，有注释和运行说明

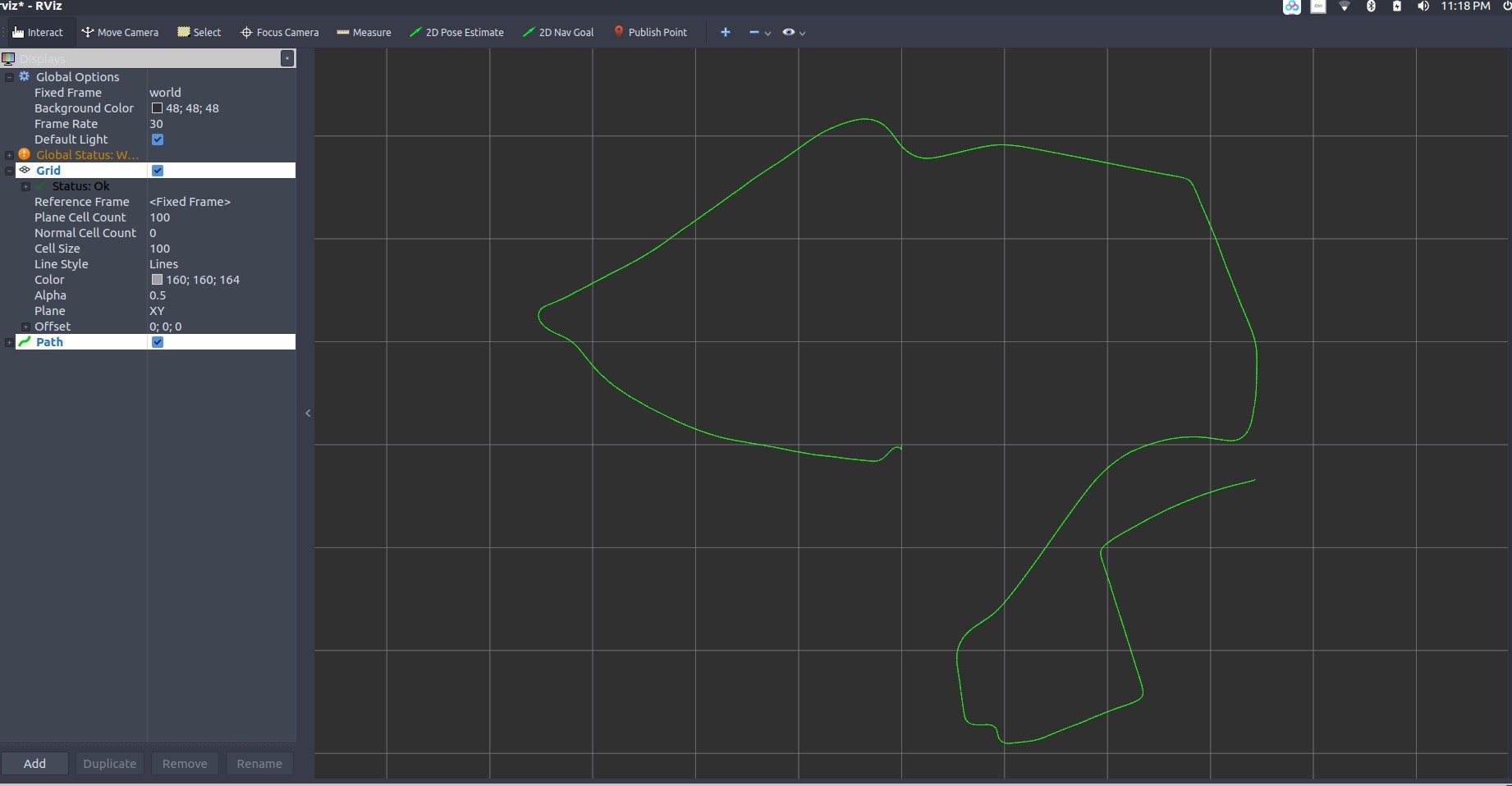
以上代码只是一个简化的示例，实际应用中可能需要根据具体的传感器特性和系统需求进行调整和优化。例如，考虑更复杂的状态模型、处理传感器数据的时间同步等问题。