六轴机器人六关节机器人六自由度机器人分析与仿真运动学动力学 aubo ur dobot

在机器人的世界里，六轴机器人，也被称为六关节机器人或六自由度机器人，可谓是明星般的存在。它们凭借高度的灵活性和精确的操作能力，在工业生产、科研探索等众多领域大放异彩。今天咱们就来深入分析分析这类机器人，顺便聊聊相关的仿真，再看看 Aubo、UR、DoBot 这些常见品牌在其中的门道。

一、六轴机器人的运动学基础

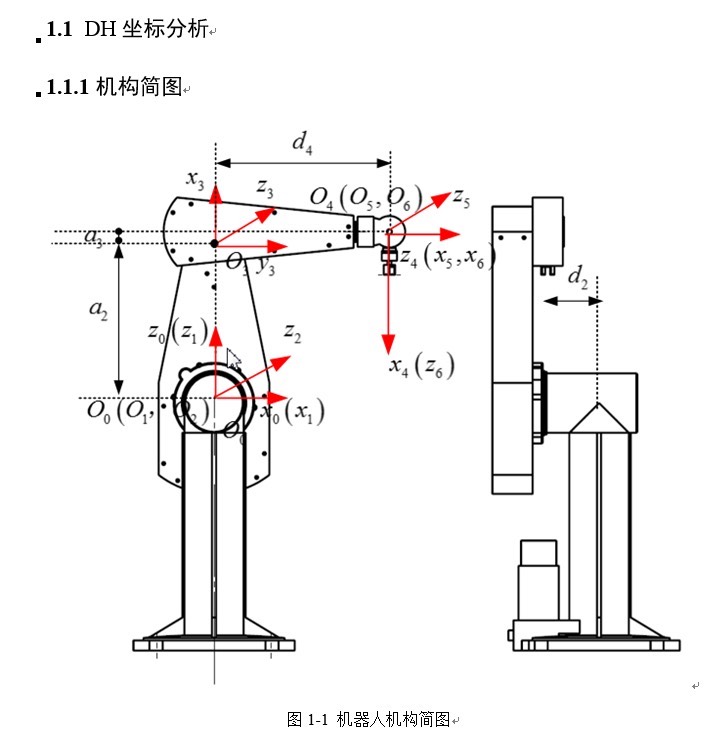
运动学主要研究机器人各关节的运动如何转化为末端执行器的空间位置和姿态。对于六轴机器人，我们通常采用 Denavit - Hartenberg（D - H）参数法来建立其运动学模型。

假设我们有一个简单的六轴机器人模型，以下是一个简化的Python代码片段，用于展示如何基于D - H参数计算齐次变换矩阵（这是运动学分析中的关键步骤）：

import numpy as np


def dh_matrix(alpha, a, d, theta):
    ct = np.cos(theta)
    st = np.sin(theta)
    ca = np.cos(alpha)
    sa = np.sin(alpha)
    T = np.array([[ct, -st * ca, st * sa, a * ct],
                  [st, ct * ca, -ct * sa, a * st],
                  [0, sa, ca, d],
                  [0, 0, 0, 1]])
    return T


# 示例D - H参数
alpha_1 = np.pi / 2
a_1 = 0
d_1 = 0.75
theta_1 = np.pi / 4

T_1 = dh_matrix(alpha_1, a_1, d_1, theta_1)
print(T_1)

在这段代码里，dh_matrix 函数接收四个D - H参数：扭角 alpha、连杆长度 a、连杆偏移 d 和关节角 theta，然后依据这些参数构建齐次变换矩阵。这个矩阵能描述相邻两个坐标系之间的位姿关系。通过依次计算各个关节的齐次变换矩阵并相乘，就能得到从机器人基座到末端执行器的总变换矩阵，从而确定末端执行器在空间中的位置和姿态。

二、动力学探秘

动力学研究的是机器人运动与作用力之间的关系。简单来说，就是要搞清楚机器人各关节需要多大的力或扭矩才能实现期望的运动。拉格朗日方程是常用的动力学建模方法之一。

六轴机器人六关节机器人六自由度机器人分析与仿真运动学动力学 aubo ur dobot

以一个简化的两关节机械臂为例，用Python代码来初步展示动力学计算的思路：

import sympy as sp


# 定义符号变量
theta1, theta2 = sp.symbols('theta1 theta2')
dtheta1, dtheta2 = sp.symbols('dtheta1 dtheta2')
ddtheta1, ddtheta2 = sp.symbols('ddtheta1 ddtheta2')
m1, m2 = sp.symbols('m1 m2')
l1, l2 = sp.symbols('l1 l2')
g = sp.symbols('g')

# 定义位置坐标
x1 = l1 * sp.cos(theta1)
y1 = l1 * sp.sin(theta1)
x2 = l1 * sp.cos(theta1) + l2 * sp.cos(theta1 + theta2)
y2 = l1 * sp.sin(theta1) + l2 * sp.sin(theta1 + theta2)

# 动能计算
T1 = 0.5 * m1 * (sp.diff(x1, theta1) * dtheta1) ** 2 + 0.5 * m1 * (sp.diff(y1, theta1) * dtheta1) ** 2
T2 = 0.5 * m2 * (sp.diff(x2, theta1) * dtheta1 + sp.diff(x2, theta2) * dtheta2) ** 2 + 0.5 * m2 * (
        sp.diff(y2, theta1) * dtheta1 + sp.diff(y2, theta2) * dtheta2) ** 2
T = T1 + T2

# 势能计算
U1 = m1 * g * y1
U2 = m2 * g * y2
U = U1 + U2

# 拉格朗日函数
L = T - U

# 计算动力学方程
tau1 = sp.diff(sp.diff(L, dtheta1), sp.Symbol('t')) - sp.diff(L, theta1)
tau2 = sp.diff(sp.diff(L, dtheta2), sp.Symbol('t')) - sp.diff(L, theta2)

print("tau1:", tau1)
print("tau2:", tau2)

这里我们先定义了关节角度、角速度、角加速度、质量、连杆长度等符号变量，接着计算了系统的动能和势能，构建拉格朗日函数，最后依据拉格朗日方程计算出每个关节所需的扭矩 tau1 和 tau2。实际的六轴机器人动力学计算要复杂得多，但基本思路是类似的。

三、仿真那些事儿

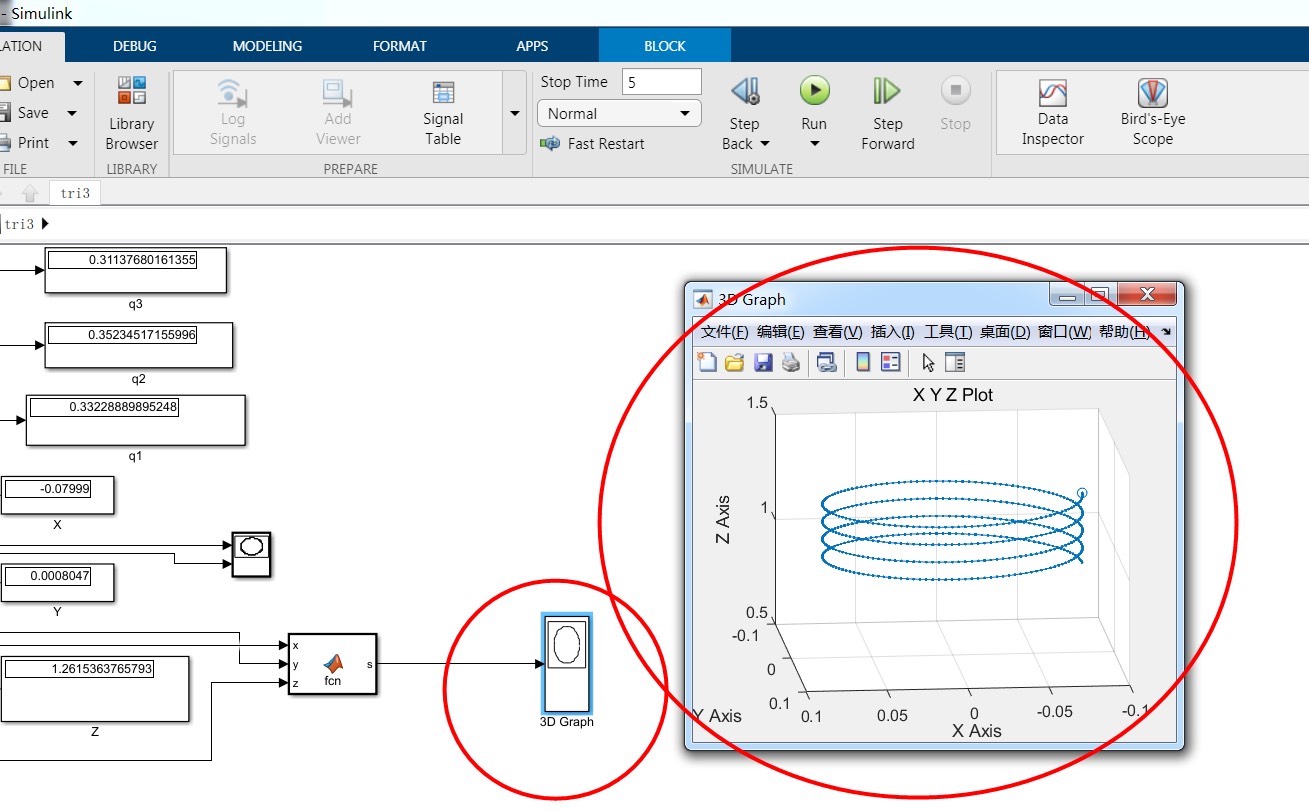
仿真在六轴机器人的研发和优化过程中起着至关重要的作用。通过仿真，我们可以在虚拟环境中测试机器人的运动规划、验证控制算法，还能提前发现潜在的问题，节省时间和成本。

在众多仿真工具中，MATLAB 的 Robotics System Toolbox 就非常强大。下面是一个简单的示例，在MATLAB中创建一个简单的六轴机器人模型并进行运动学仿真：

% 创建六轴机器人模型
L(1) = robotics.RevoluteJoint('theta',0,'d',0.75,'a',0,'alpha',pi/2);
L(2) = robotics.RevoluteJoint('theta',-pi/2,'d',0,'a',0.35,'alpha',0);
L(3) = robotics.RevoluteJoint('theta',0,'d',0,'a',1.25,'alpha',0);
L(4) = robotics.RevoluteJoint('theta',-pi/2,'d',1.5,'a',-0.054,'alpha',pi/2);
L(5) = robotics.RevoluteJoint('theta',pi/2,'d',0,'a',0,'alpha',-pi/2);
L(6) = robotics.RevoluteJoint('theta',0,'d',0.303,'a',0,'alpha',0);
robot = robotics.RigidBodyTree;
addBody(robot, L(1), 'base');
for i = 2:6
    addBody(robot, L(i), L(i - 1).Name);
end

% 定义关节角度序列
q1 = [0 0 0 0 0 0];
q2 = [pi/4 pi/4 pi/4 pi/4 pi/4 pi/4];
q_path = jtraj(q1, q2, 50);

% 进行仿真
figure
show(robot,q_path(1,:))
axis([-2 2 -2 2 0 3])
for i = 1:size(q_path, 1)
    show(robot,q_path(i,:))
    drawnow
end

这段MATLAB代码首先创建了一个六轴机器人模型，定义了每个关节的D - H参数。然后指定了两个关节角度配置 q1 和 q2，并通过 jtraj 函数生成从 q1 到 q2 的平滑关节角度路径。最后在图形窗口中显示机器人沿着该路径运动的仿真动画。

四、Aubo、UR、DoBot品牌特色

1. Aubo（遨博）：Aubo的机器人以其易用性和较高的性价比在市场上占有一席之地。在运动学和动力学控制方面，Aubo 注重优化算法，使得机器人在高速运动时也能保持较好的稳定性和精度。例如其协作机器人系列，在与人协同工作场景下，通过对动力学的精确调控，确保安全且高效的操作。
2. UR（Universal Robots）：UR 的六轴机器人以灵活编程和友好的人机交互著称。在运动学规划上，它具备强大的路径优化能力，能够快速规划出最优运动轨迹，减少运动时间和能耗。动力学方面，UR 机器人采用先进的力矩控制技术，使得机器人在接触外界物体时能够精确感知并做出合理反应，这在诸如装配、打磨等精细任务中表现出色。
3. DoBot（大族机器人）：DoBot 的产品多侧重于桌面型机器人领域，小巧灵活且价格亲民。在运动学设计上，针对桌面操作场景进行了优化，能实现快速精准的定位。动力学控制方面，通过合理的结构设计和算法优化，使得机器人在小负载情况下也能稳定高效运行，广泛应用于教育、科研、轻量生产等领域。

六轴机器人的运动学与动力学分析以及仿真，是一个充满挑战与乐趣的领域。不同品牌的机器人基于这些理论基础，展现出各自独特的魅力和优势，推动着机器人技术不断向前发展，为我们的生产生活带来更多便利和创新。