【leetcode】力扣经典算法题解：动态规划全攻略

本文分享了力扣（LeetCode）三道经典动态规划题目的详细解析：不同路径问题：通过构建dp表，分析状态转移方程，解决机器人网格移动路径计数问题；下降路径最小和：讨论方形矩阵中寻找最小下降路径和的动态规划解法；地下城游戏：重点分析骑士救公主所需最低初始健康点数的逆向动态规划思路。每道题目都包含完整的解题步骤（状态表示、转移方程、初始化、代码实现）和关键注意事项，帮助读者掌握动态规划的核心思

GGBondlctrl

410人浏览 · 2026-01-22 19:03:52

GGBondlctrl · 2026-01-22 19:03:52 发布

📚️前言
🌟 本期内容亮点：我们将深入解析力扣（LeetCode）上的几道经典算法题，涵盖不同难度和题型，帮助大家掌握解题思路和代码实现技巧。无论是准备面试还是提升算法能力，这些题解都能为你提供实用参考~

🌈 更多精彩内容：

欢迎访问小编的主页：GGBondlctrl-CSDN博客（点击跳转）
🔥 你的支持很重要：
如果觉得内容对你有帮助，别忘了点赞👍 + 收藏⭐！你的鼓励是小编持续创作优质内容的动力~

🎆 直接进入正题：下面我们将从题目描述、解题思路、代码实现（附详细注释）和复杂度分析等方面，逐一拆解这几道力扣题目，助你高效攻克算法难关！

1.前言

说实话，小编已经很久没有更新过自己的博客了，所以很抱歉各位支持我的的uu们；在未来小编会重操旧业，谢谢各位uu~~~

2.不同路径

2.1题目描述

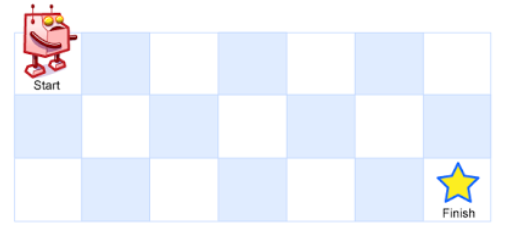
一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

2.2题目解析

针对我们所有的动态规划问题其实都有一下几种结题步骤，这是动态规划的题解重要部分

1.状态表示

2.状态转移方程

3.初始化

4.填表顺序

5.返回对应的值

状态表示

所以的路径问题我们可以依照其中一个位置来进行状态表示，根据题意就是两种：

以i，j位置为结尾，到达这个位置的总共路径；

以i，j位置为起点，到达右下角位置的总共路径；

那么我们以第一种状态表示来看，是否可以得到状态转移方程；

这里我们可以发现到达某一个位置只有从这个位置的上面和左边出发；那么前一个位置的dp[i][j]表示的就是到这个位置的总路径，那么我只需要把左边和上面的位置总路径相加，就是到达目标位置的总路径

状态转移方程

由上面我们分析出一个情况就是dp[i][j]（到达这个位置的总路径）等于上面和左边dp的和

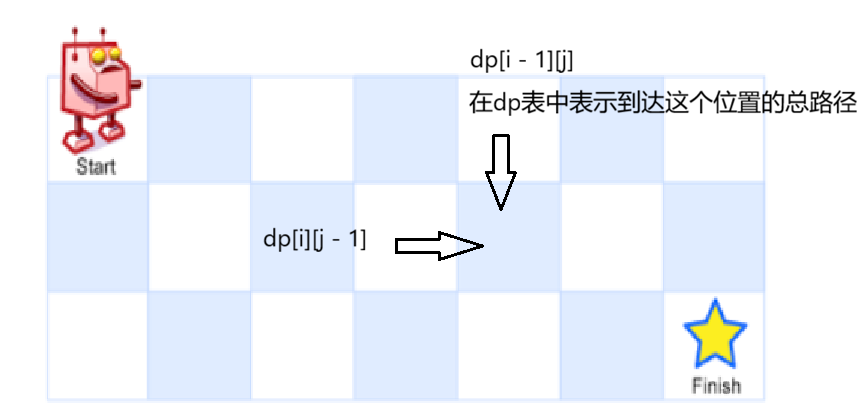
所以得出我们的状态转移方程就是

dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

初始化

这里的初始化就是为了防止i - 1，或者是j - 1出现越界的情况，那么我们这里可以往外进行延伸，这里为啥要进行延伸呢？其实主要是为了方便初始化；假如直接按原表的行列数进行创建dp，在求边界的时候可能直接依赖前一个位置，可能就有点麻烦；

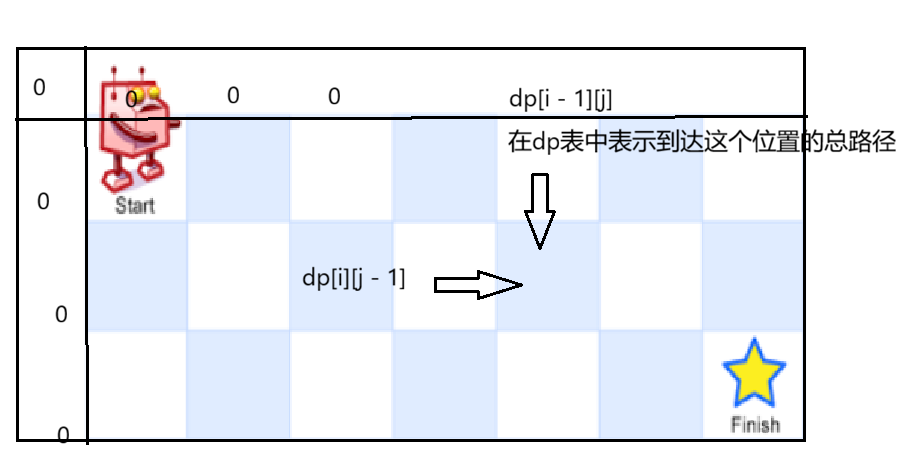
这里为啥在添加行列的时候初始化为0呢，注意我们在初始化额外添加的行列的时候，不可以影响我们填表的情况；所以我们以机器人在位置，dp[1][1] 就是自己本身只有dp[i - 1][j] + dp[i][j - 1] == 1，所以我们这里的0,1或者是1,0，位置就是不是0，就初始化为1即可

那么其他边界位置，等于上或者左边的数值，那么这里就不可以影响边界位置的总路径值，所以初始化为1；

返回值

返回值就是到达星星位置的dp[i][j]位置，表示到达星星位置的总路径；所以直接返回这个位置即可

2.3题目代码

实例代码如下：

class Solution {
    public int uniquePaths(int m, int n) {
        //创建搭配dp表
        int[][] dp = new int[m + 1][n + 1];
        //初始化
        for(int i = 0; i < m + 1; i ++){
            dp[i][0] = 0;
        }
        for(int j = 0; j < n + 1; j ++){
            dp[0][j] = 0;
        }
        dp[0][1] = 1;

        //填表
        for(int i = 1; i < m + 1; i ++){
            for(int j = 1; j < n + 1; j ++){
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m][n];
    }
}

这里要注意我们规定的二维数组的行列数目；所以返回的实际星星位置为m,n位置，因为我们多添加了一行和一列；

3.下降路径最小和

3.1题目描述

给你一个 n x n 的方形整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

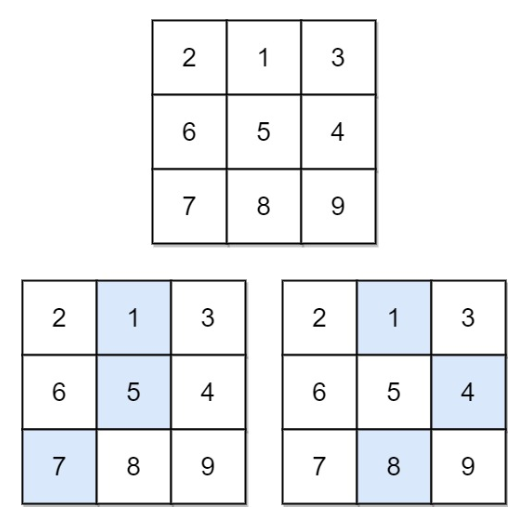
其实就是选定一个格子i，j后，后序向下降落的过程只能选择下一行i + 1,j - 1；i + 1, j; i + 1,j + 1位置了；

3.2题目解析

状态表示

和上面一样，我们按照一个位置来看，就是到达i，j位置的最小下降路径和；那么我们可以推测出这里的状态转移方程

状态转移方程

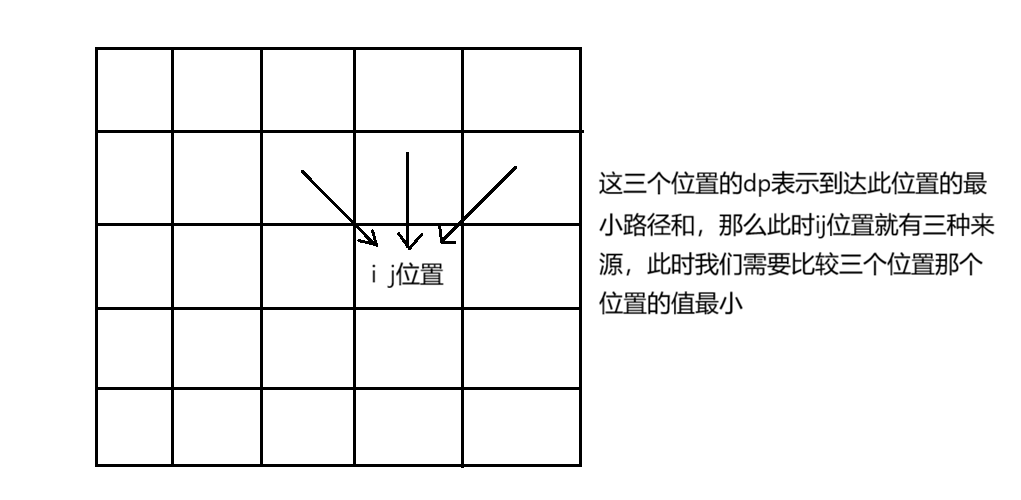
那么我们可以推断出状态转移方程：

dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1],dp[i - 1][j]),dp[i - 1][j + 1]) + matrix[i - 1][j - 1];

这里还要加上本身位置的路径上对应的值

初始化

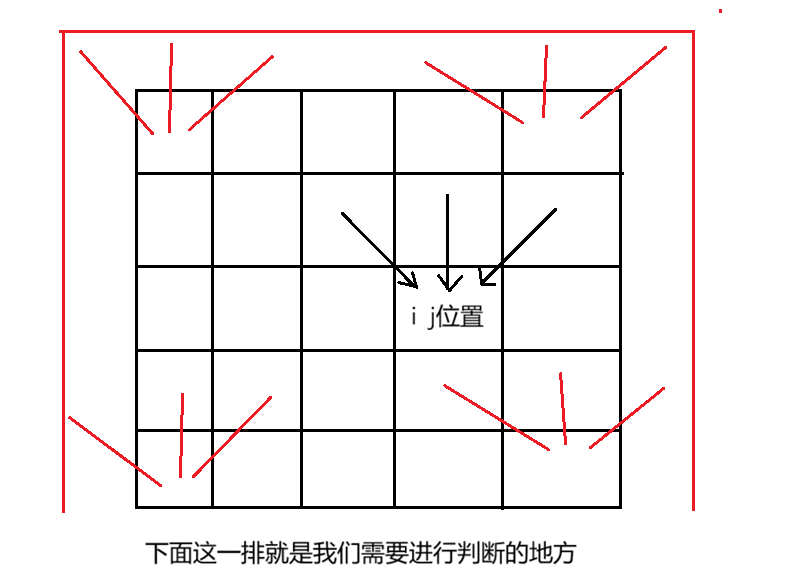
下图就是可能会出现越界的情况，所以要对这些位置进行初始化，那么我们希望的是不会影响不越界位置的判断，此时求的min，所以我们初始化这些格子为正无穷大；

但是注意了最上面一行的来源都是越界的地方，这里根据状态转移方程来看，到达此位置就是自己本身，所以初始化最上面额外添加的一行的值就是0；

返回值

很明显我们要知道到达dp表最下面一行的最小值，所以返回的应该是最后一行的数值中最小的那个；

3.3题目代码

代码如下所示：

class Solution {
    public int minFallingPathSum(int[][] matrix) {
        //创建表
        int m = matrix.length;
        int n = matrix[0].length;
        int[][] dp = new int[m + 1][n + 2];
        //初始化
        for(int i = 1; i < m + 1; i ++){
            dp[i][0] = Integer.MAX_VALUE;
            dp[i][n + 1] = Integer.MAX_VALUE;
        }
        //填表
        for(int i = 1; i < m + 1; i ++){
            for(int j = 1; j < n + 1; j ++){
                dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1],dp[i - 1][j]),dp[i - 1][j + 1]) + matrix[i - 1][j - 1];
            }
        }
        int min = Integer.MAX_VALUE;
        for(int j = 1; j < n + 1; j ++ ){
            if(min > dp[m][j]){
                min = dp[m][j];
            }
        }
        return min;
    }
}

代码编写分为：创建dp表，初始化，以及最后的填表，和返回目标值即可；

4.地下城游戏

4.1题目描述

恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快解救公主，骑士决定每次只向右或向下移动一步。

返回确保骑士能够拯救到公主所需的最低初始健康点数。

注意：任何房间都可能对骑士的健康点数造成威胁，也可能增加骑士的健康点数，包括骑士进入的左上角房间以及公主被监禁的右下角房间。

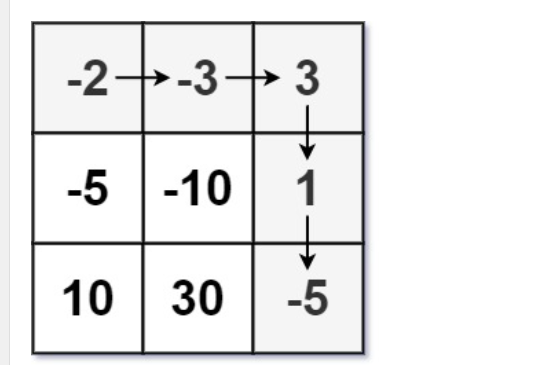
4.2题目解析

状态表示

这里还是可以按照上述的讲解来看，我们规定某一个位置，即dp[i][j]表示到达ij位置的最小血量要求；

但是这个状态表示是正确的吗？

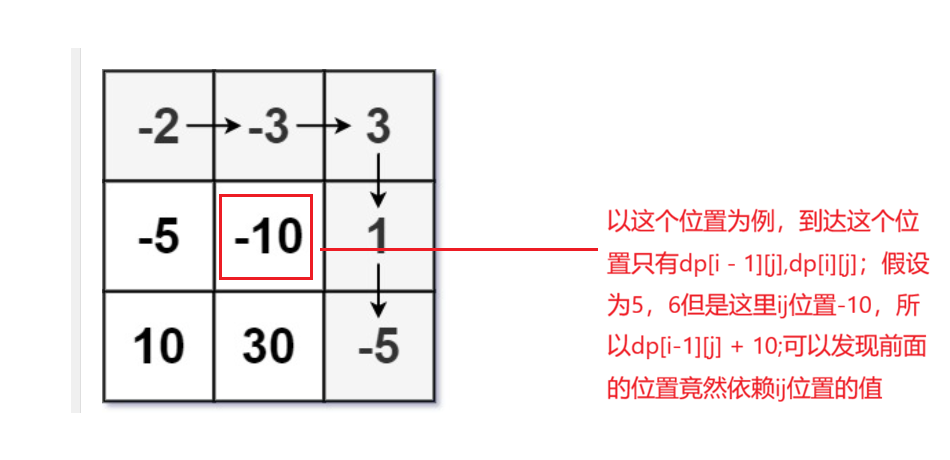
以这个位置为例，到达这个位置只有dp[i - 1][j],dp[i][j]；假设为5，6但是这里ij位置-10，所以dp[i-1][j] + 10;可以发现前面的位置竟然依赖ij位置的值；依次类推，我们是不是还要依赖更加靠后的位置，所以这种状态表示根本不是正确的；

所以正确的应该是：从i,j位置出发，到达终点所需的初始最定健康点数

状态转移方程

我们假设此位置为x的健康点数；那么有x + dungeon[i][j] >= Math.min(dp[i][j + 1],dp[i + 1][j])

这里表示这个位置扣除血量后，必须满足下一步格子的所需最小血量；

并且要注意；假如格子为正数，x = Math.min(dp[i][j + 1],dp[i + 1][j]) - dungeon[i][j]为负数，就说明骑士在吃血包，这里为负数，但是这是不符合题意的，所以这里最小为1，在执行上述状态转移方程后，还要与1进行比较；（骑士本身的血量最少为1）

初始化

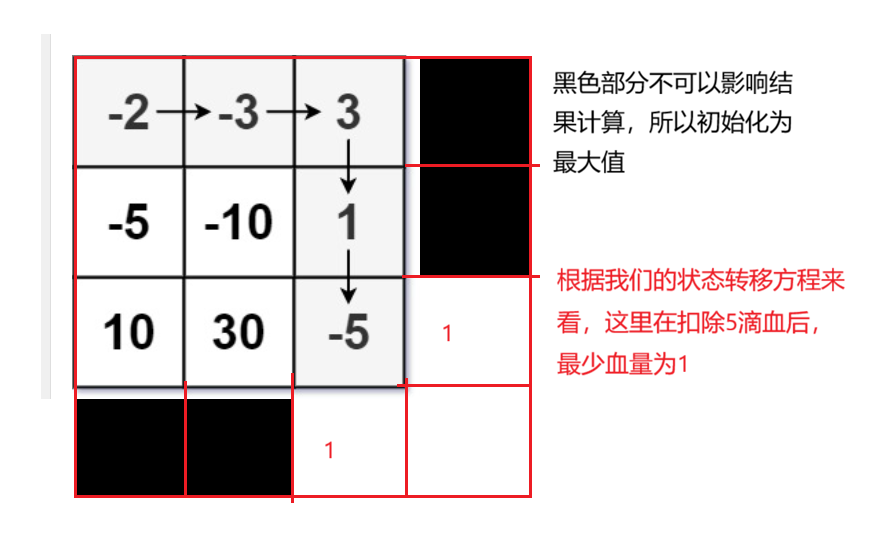
返回值

返回值和之前的题相反，按照题意返回的值就是dp[0][0]；

4.3题目代码

代码如下所示：

class Solution {
    public int calculateMinimumHP(int[][] dungeon) {
        //创建dp表
        int m = dungeon.length;
        int n = dungeon[0].length;
        int[][] dp = new int[m + 1][n + 1];

        //初始化
        for(int i = 0; i < m + 1; i ++){
            dp[i][n] = Integer.MAX_VALUE;
        }
        for(int j = 0; j < n + 1; j ++){
            dp[m][j] = Integer.MAX_VALUE;
        }
        dp[m - 1][n] = 1;
        dp[m][n - 1] = 1;

        //填表
        for(int i = m - 1; i >= 0; i --){
            for(int j = n - 1; j >= 0; j -- ){
                dp[i][j] = Math.min(dp[i + 1][j],dp[i][j + 1]) - dungeon[i][j];
                dp[i][j] = Math.max(dp[i][j], 1);
            }
        }
        return dp[0][0];
    }
}