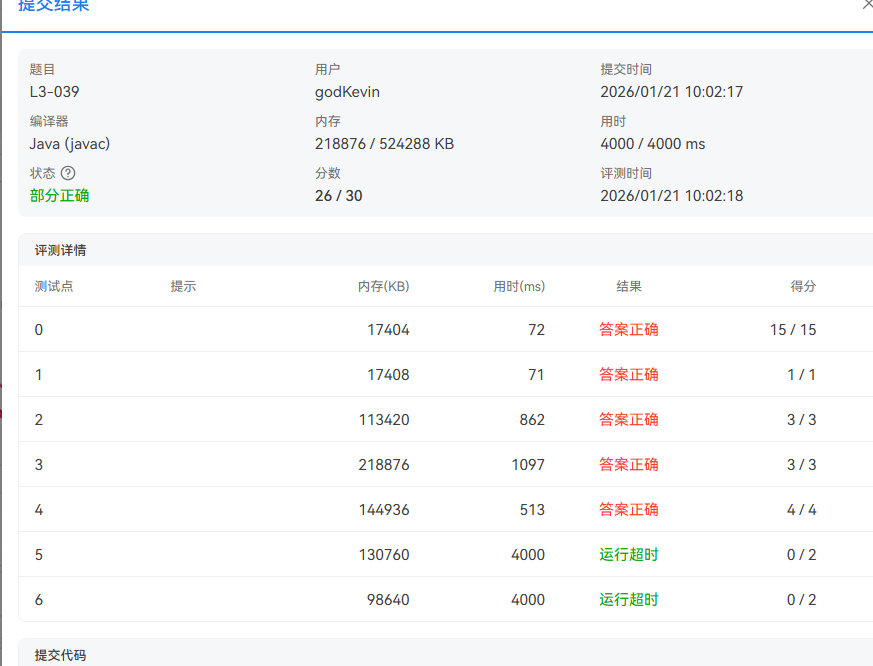
PTA团体程序设计天梯赛 L3-039 攀岩 （30/30）（Delaunay 三角剖分）（C++ Java双版本）
·
九条可怜最近接触到了攀岩这项运动。作为一名运动量接近为零的家里蹲，相比于动手攀岩，可怜显然更加享受攀岩运动中动脑的部分，即对攀岩路线的规划。
为了只动脑，可怜设计了一个简易的攀岩机器人来帮她动手。这个机器人由一个核心（大小可以忽略不计）和三个长度至多为 r 的可伸缩机械臂组成，如下图所示：
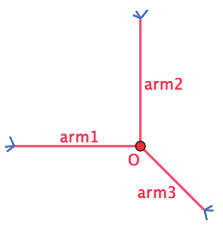
一面攀岩墙可以看成一个二维的无穷平面，上面有 n 个不同位置的岩点 p1,…,pn。在攀岩开始时，机器人的两个机械臂需要分别抓住岩点 p1 和 p2，而其核心和第三个机械臂可以在任意位置。攀岩的目标是让机器人有两支机械臂同时抓握住岩点 pn。
在攀岩过程中，机器人需要保证每时每刻都有两支机械臂抓握住两个不同的岩点。在满足这点的情况下，机器人可以在机械臂长度允许的情况下进行如下移动：
- 连续地将核心的位置从当前位置移动到任意位置。
- 用第三条机械臂抓握住一个岩点（可以与某条其他机械臂抓住相同的岩点）。
- 让一条机械臂松开其抓握的岩点。注意，只有当另外两条机械臂已经抓握住不同岩点时，才能进行这项操作。
注：我们假设岩点的大小是无穷小，不会影响机器人的移动，比如机械臂、核心轨迹都可以经过岩点。
下面是一个攀岩过程的例子，假设平面上有四个岩点，坐标分别是 (0,0),(1,0),(0,1),(1,2)，则下面展示了一个 r=2 时，即机械臂长度至多为 2 时的攀岩方案。
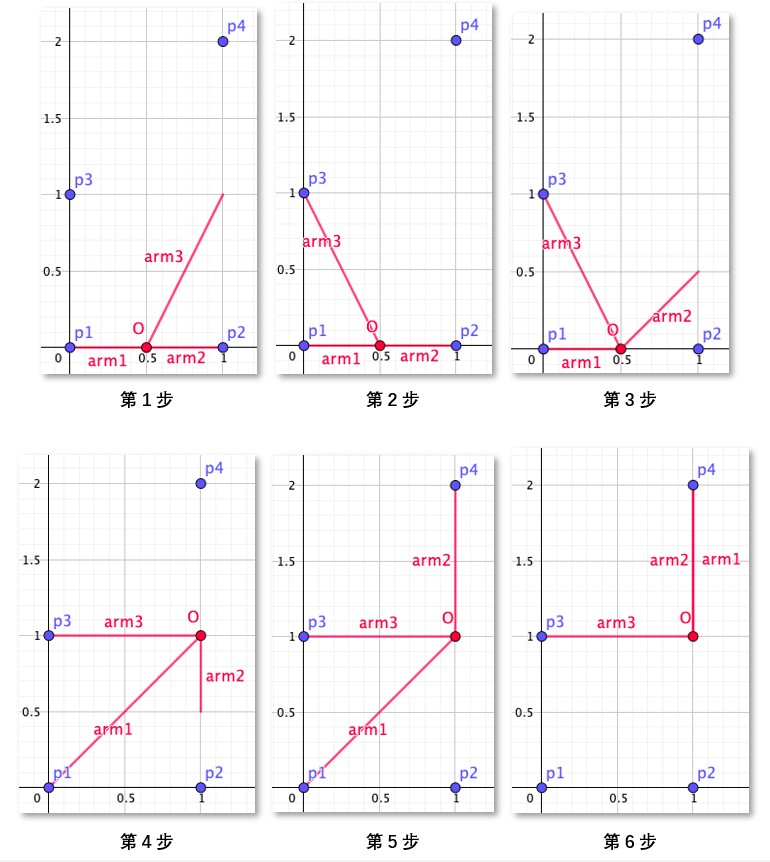
- 初始时，可怜将机器人的核心放在 (0.5,0) 处，第三根手臂随意地放在 (1,1) 处。
- 机器人的第三机械臂抓握住岩点 p3。
- 机器人的第二机械臂松开，并移动到 (1,0.5) 处。
- 机器人的核心移动至 (1,1)，此时第一机械臂的长度到达极限 2。
- 机器人的第二机械臂抓握住岩点 p4。
- 机器人的第一机械臂松开，并抓握住岩点 p4，完成攀岩目标。
显然，机器人的机械臂长度越短，对可怜的路径规划能力要求越高。但是这个机械臂的长度也不能太短，不然机器人可能无论如何都无法完成攀岩任务。比如在上述任务中，如果机械臂长度小于 0.5，那么机器人将无法同时抓握 p1 和 p2，这意味着它连开始攀岩都无法做到，更别说完成攀岩任务了。
因此，为了在合理范围内尽可能地挑战自己的大脑，可怜希望你对于攀岩馆中的每一项攀岩任务，都帮她计算（在可能完成攀岩任务的前提下）机械臂的最短长度是多少。
输入格式:
第一行输入一个整数 t (t≤100)，表示攀岩馆内攀岩任务的数量。
每个任务的第一行都是一个整数 n (3≤n≤1500)，表示攀岩任务涉及的岩点数量。
接下来 n 行，每行两个整数 (xi,yi)，表示第 i 个岩点的坐标。输入保证 0≤xi,yi≤106 且同一个攀岩任务中的岩点坐标两两不同。
输入保证满足 n>100 的数据不超过 3 组。
输出格式:
对于每个攀岩任务输出一行一个浮点数，表示最短可能的机械臂长度。你的答案在绝对误差或者相对误差不超过 10−6 的情况下都会被视为正确。
输入样例:
4
4
0 0
1 0
0 1
1 2
4
0 0
2 0
0 3
2 2
7
0 0
1 0
2 0
2 1
2 2
1 2
0 2
15
13 2
13 3
12 44
6 17
4 71
14 58
4 49
2 51
8 37
1 18
5 43
5 35
1 84
10 23
13 69
输出样例:
0.99999999498
1.41421355524
1.00000000498
10.13227667717
样例解释
第一组数据和题面中的攀岩任务一致，其最小机械臂长度为 1，而样例输出的答案在 10−6 的误差范围内，故会被视为正确。
下面给出了一个机械臂长度为 1 时的攀岩方案。攀岩开始时，机器人的核心与岩点 p1 重叠，第三机械臂在长度为 0 的情况下抓住了这个岩点，且第一机械臂额外抓住了岩点 p3。接着，第三机械臂松开岩点 p1，并随着核心移动至点 (1,1)。然后，第三机械臂伸出并抓握住岩点 p4。最后，第二机械臂松开岩点 p2 并同样抓握住岩点 p4，完成攀岩任务。
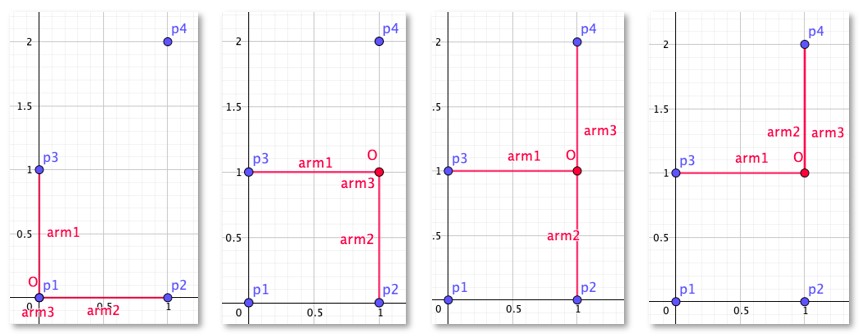
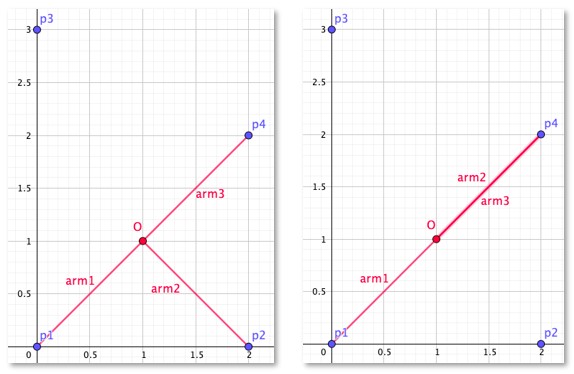
第二组数据中，最小机械臂长度为 2，下图展示了一个对应的攀岩方案。攀岩开始时，机器人的核心位于 (1,1) 且三个机械臂分别抓握住岩点 p1,p2 和 p4。随后，第二机械臂松开点 p2 并抓握住岩点 p4，完成攀岩任务。注意到此攀岩方案全程没有使用岩点 p3，这也是被允许的：攀岩任务中不要求使用所有的岩点。
代码长度限制
16 KB
时间限制
4000 ms
内存限制
512 MB
栈限制
8192 KB
import java.io.*;
import java.util.*;
public class Main {
// === 快读 ===
static final int SZ = 1 << 18;
static byte[] ibuf = new byte[SZ];
static int ip = 0, il = 0;
static InputStream is = System.in;
static int rb() throws IOException {
if (ip >= il) { il = is.read(ibuf); ip = 0; }
return il == -1 ? -1 : ibuf[ip++];
}
static int ri() throws IOException {
int c = rb(), x = 0;
while (c < '0' || c > '9') c = rb();
while (c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = rb(); }
return x;
}
static long rl() throws IOException {
int c = rb(); long x = 0;
while (c < '0' || c > '9') c = rb();
while (c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = rb(); }
return x;
}
// === Delaunay 三角剖分 (Guibas-Stolfi) ===
// Quad-edge 用数组: 每条边占 4 个槽 (e, e+1=rot, e+2=rev, e+3=rot of rev)
// org[e], onext[e], used[e]
static final int QPOOL = 8_000_000;
static long[] qox = new long[QPOOL], qoy = new long[QPOOL];
static int[] qid = new int[QPOOL]; // 原始点 id
static int[] onext = new int[QPOOL];
static boolean[] used = new boolean[QPOOL];
static int qcnt;
static void qinit() { qcnt = 0; }
static int rot(int e) { return (e & ~3) | ((e + 1) & 3); }
static int rev(int e) { return (e & ~3) | ((e + 2) & 3); }
static int lnext(int e) { return rot(onext[rot(rev(e))]); }
static int oprev(int e) { return rot(onext[rot(e)]); }
static long destX(int e) { return qox[rev(e)]; }
static long destY(int e) { return qoy[rev(e)]; }
static int destId(int e) { return qid[rev(e)]; }
static int makeEdge(long ax, long ay, int ai, long bx, long by, int bi) {
int e = qcnt; qcnt += 4;
qox[e] = ax; qoy[e] = ay; qid[e] = ai;
qox[e|2] = bx; qoy[e|2] = by; qid[e|2] = bi;
qox[e|1] = qoy[e|1] = qox[e|3] = qoy[e|3] = (long) 1e18;
qid[e|1] = qid[e|3] = -1;
onext[e] = e; onext[e|2] = e|2;
onext[e|1] = e|3; onext[e|3] = e|1;
used[e] = used[e|1] = used[e|2] = used[e|3] = false;
return e;
}
static void splice(int a, int b) {
int t1 = onext[rot(onext[a])], t2 = onext[rot(onext[b])];
int t3 = onext[a], t4 = onext[b];
onext[rot(onext[a])] = t2;
onext[rot(onext[b])] = t1;
onext[a] = t4;
onext[b] = t3;
}
static void delEdge(int e) {
splice(e, oprev(e));
splice(rev(e), oprev(rev(e)));
}
static int connect(int a, int b) {
int e = makeEdge(destX(a), destY(a), destId(a), qox[b], qoy[b], qid[b]);
splice(e, lnext(a));
splice(rev(e), b);
return e;
}
static long cross(long ox, long oy, long ax, long ay, long bx, long by) {
return (ax - ox) * (by - oy) - (ay - oy) * (bx - ox);
}
static boolean leftOf(long px, long py, int e) {
return cross(qox[e], qoy[e], destX(e), destY(e), px, py) > 0;
}
static boolean rightOf(long px, long py, int e) {
return cross(qox[e], qoy[e], destX(e), destY(e), px, py) < 0;
}
// in_circle: 用 double 计算行列式 (坐标 ≤ 10^6, 精度足够)
static boolean inCircle(long ax, long ay, long bx, long by,
long cx, long cy, long dx, long dy) {
double dax = ax - dx, day = ay - dy, das = dax * dax + day * day;
double dbx = bx - dx, dby = by - dy, dbs = dbx * dbx + dby * dby;
double dcx = cx - dx, dcy = cy - dy, dcs = dcx * dcx + dcy * dcy;
double det = dax * (dby * dcs - dcy * dbs)
- dbx * (day * dcs - dcy * das)
+ dcx * (day * dbs - dby * das);
return det > 0;
}
// Delaunay build (divide & conquer), 返回 {leftEdge, rightEdge}
static long[] spx, spy; static int[] sid; // 排序后的点
static int[] buildRes = new int[2]; // 返回值复用
static void buildTr(int l, int r) {
if (r - l + 1 == 2) {
int e = makeEdge(spx[l], spy[l], sid[l], spx[r], spy[r], sid[r]);
buildRes[0] = e; buildRes[1] = rev(e); return;
}
if (r - l + 1 == 3) {
int a = makeEdge(spx[l], spy[l], sid[l], spx[l+1], spy[l+1], sid[l+1]);
int b = makeEdge(spx[l+1], spy[l+1], sid[l+1], spx[r], spy[r], sid[r]);
splice(rev(a), b);
long sg = cross(spx[l], spy[l], spx[l+1], spy[l+1], spx[r], spy[r]);
if (sg == 0) { buildRes[0] = a; buildRes[1] = rev(b); return; }
int c = connect(b, a);
if (sg > 0) { buildRes[0] = a; buildRes[1] = rev(b); }
else { buildRes[0] = rev(c); buildRes[1] = c; }
return;
}
int mid = (l + r) / 2;
buildTr(l, mid);
int ldo = buildRes[0], ldi = buildRes[1];
buildTr(mid + 1, r);
int rdi = buildRes[0], rdo = buildRes[1];
// 找下切线
while (true) {
if (leftOf(qox[rdi], qoy[rdi], ldi)) { ldi = lnext(ldi); continue; }
if (rightOf(qox[ldi], qoy[ldi], rdi)) { rdi = onext[rev(rdi)]; continue; }
break;
}
int basel = connect(rev(rdi), ldi);
if (qox[ldi] == qox[ldo] && qoy[ldi] == qoy[ldo]) ldo = rev(basel);
if (qox[rdi] == qox[rdo] && qoy[rdi] == qoy[rdo]) rdo = basel;
// 合并
while (true) {
int lc = onext[rev(basel)];
boolean lv = rightOf(destX(lc), destY(lc), basel);
if (lv) {
while (inCircle(destX(basel), destY(basel), qox[basel], qoy[basel],
destX(lc), destY(lc), destX(onext[lc]), destY(onext[lc]))) {
int t = onext[lc]; delEdge(lc); lc = t;
}
lv = rightOf(destX(lc), destY(lc), basel);
}
int rc = oprev(basel);
boolean rv = rightOf(destX(rc), destY(rc), basel);
if (rv) {
while (inCircle(destX(basel), destY(basel), qox[basel], qoy[basel],
destX(rc), destY(rc), destX(oprev(rc)), destY(oprev(rc)))) {
int t = oprev(rc); delEdge(rc); rc = t;
}
rv = rightOf(destX(rc), destY(rc), basel);
}
if (!lv && !rv) break;
if (!lv || (rv && inCircle(destX(lc), destY(lc), qox[lc], qoy[lc],
qox[rc], qoy[rc], destX(rc), destY(rc))))
basel = connect(rc, rev(basel));
else
basel = connect(rev(basel), rev(lc));
}
buildRes[0] = ldo; buildRes[1] = rdo;
}
// 提取三角形, 返回 int[][3] (原始点 id)
static int[][] triangulate(long[] px, long[] py, int[] id, int n) {
if (n < 3) return new int[0][];
qinit();
// 排序
Integer[] ord = new Integer[n];
for (int i = 0; i < n; i++) ord[i] = i;
Arrays.sort(ord, (a, b) -> px[a] != px[b] ? Long.compare(px[a], px[b]) : Long.compare(py[a], py[b]));
spx = new long[n]; spy = new long[n]; sid = new int[n];
for (int i = 0; i < n; i++) { spx[i] = px[ord[i]]; spy[i] = py[ord[i]]; sid[i] = id[ord[i]]; }
buildTr(0, n - 1);
int le = buildRes[0];
// 遍历三角形
int e = le;
ArrayList<Integer> stk = new ArrayList<>();
stk.add(e);
while (cross(qox[e], qoy[e], destX(e), destY(e),
destX(onext[e]), destY(onext[e])) > 0) e = onext[e];
// BFS 遍历面
ArrayList<int[]> tris = new ArrayList<>();
ArrayList<Integer> triIds = new ArrayList<>(); // 三角形顶点 id
// 用 add 函数遍历
int stkIdx = 0;
// 先处理第一个面
{
int cur = e;
do {
used[cur] = true;
triIds.add(qid[cur]);
stk.add(rev(cur));
cur = lnext(cur);
} while (cur != e);
}
triIds.clear(); // 第一个面可能是外部面
stkIdx = 0;
while (stkIdx < stk.size()) {
e = stk.get(stkIdx++);
if (used[e]) continue;
int cur = e;
int cnt = 0;
int[] tri = new int[3];
do {
used[cur] = true;
if (cnt < 3) tri[cnt] = qid[cur];
cnt++;
stk.add(rev(cur));
cur = lnext(cur);
} while (cur != e);
if (cnt == 3) tris.add(tri);
}
return tris.toArray(new int[0][]);
}
// === 主算法 ===
static final int MAXN = 1505;
static final double INF = 1e18;
static double[][] d2 = new double[MAXN][MAXN];
static double[][] best = new double[MAXN][MAXN];
static int[][] adj; // Delaunay 邻居
// 索引堆
static int[] pq, qp; static int pqSz;
static double[] key;
static void swim(int k) {
while (k > 1 && key[pq[k >> 1]] > key[pq[k]]) {
int t = pq[k]; pq[k] = pq[k >> 1]; pq[k >> 1] = t;
qp[pq[k]] = k; qp[pq[k >> 1]] = k >> 1;
k >>= 1;
}
}
static void sink(int k) {
while ((k << 1) <= pqSz) {
int j = k << 1;
if (j < pqSz && key[pq[j]] > key[pq[j + 1]]) j++;
if (key[pq[k]] <= key[pq[j]]) break;
int t = pq[k]; pq[k] = pq[j]; pq[j] = t;
qp[pq[k]] = k; qp[pq[j]] = j;
k = j;
}
}
static void pqPush(int id, double c) {
if (c < key[id]) {
key[id] = c;
if (qp[id] != -1) swim(qp[id]);
else { qp[id] = ++pqSz; pq[pqSz] = id; swim(pqSz); }
}
}
static int pqPop() {
int r = pq[1];
int t = pq[1]; pq[1] = pq[pqSz]; pq[pqSz] = t;
qp[pq[1]] = 1; qp[r] = -1;
pqSz--;
if (pqSz > 0) sink(1);
return r;
}
static double circumR2(int u, int v, int k) {
double a2 = d2[u][v], b2 = d2[u][k], c2 = d2[v][k];
double mx, m1, m2;
if (a2 >= b2 && a2 >= c2) { mx = a2; m1 = b2; m2 = c2; }
else if (b2 >= c2) { mx = b2; m1 = a2; m2 = c2; }
else { mx = c2; m1 = a2; m2 = b2; }
if (m1 + m2 <= mx) return mx * 0.25;
double tt = m1 + m2 - mx;
double den = 4.0 * m1 * m2 - tt * tt;
return mx * m1 * m2 / den;
}
static void solve() throws IOException {
int n = ri();
long[] px = new long[n], py = new long[n];
for (int i = 0; i < n; i++) { px[i] = rl(); py[i] = rl(); }
if (n < 3) {
if (n == 2) {
double dx = px[0] - px[1], dy = py[0] - py[1];
System.out.printf("%.10f%n", Math.sqrt(dx * dx + dy * dy) * 0.5);
} else System.out.printf("%.10f%n", 0.0);
return;
}
// 距离矩阵
for (int i = 0; i < n; i++) {
d2[i][i] = 0;
for (int j = i + 1; j < n; j++) {
long dx = px[i] - px[j], dy = py[i] - py[j];
d2[i][j] = d2[j][i] = (double)(dx * dx + dy * dy);
}
}
// Delaunay
int[] ids = new int[n]; for (int i = 0; i < n; i++) ids[i] = i;
int[][] tris = triangulate(px, py, ids, n);
// 邻接表
adj = new int[n][];
@SuppressWarnings("unchecked")
ArrayList<Integer>[] tmp = new ArrayList[n];
for (int i = 0; i < n; i++) tmp[i] = new ArrayList<>();
for (int[] tr : tris) {
int a = tr[0], b = tr[1], c = tr[2];
tmp[a].add(b); tmp[a].add(c);
tmp[b].add(a); tmp[b].add(c);
tmp[c].add(a); tmp[c].add(b);
}
for (int i = 0; i < n; i++) {
TreeSet<Integer> s = new TreeSet<>(tmp[i]);
adj[i] = new int[s.size()]; int j = 0;
for (int v : s) adj[i][j++] = v;
}
// 初始化
for (int i = 0; i < n; i++) Arrays.fill(best[i], 0, n, INF);
int lim = n * n;
key = new double[lim]; Arrays.fill(key, 0, lim, INF);
qp = new int[lim]; Arrays.fill(qp, 0, lim, -1);
pq = new int[lim + 1]; pqSz = 0;
double sc = d2[0][1] * 0.25;
best[0][1] = best[1][0] = sc;
pqPush(0 * n + 1, sc);
pqPush(1 * n + 0, sc);
double ans = INF;
while (pqSz > 0) {
int id = pqPop();
double r2 = key[id];
if (r2 >= ans) continue;
int u = id / n, v = id % n;
if (r2 > best[u][v]) continue;
if (u == n - 1 || v == n - 1) { ans = r2; break; }
for (int k : adj[u]) {
if (k == u || k == v) continue;
double cr2 = circumR2(u, v, k);
double cost = cr2 > r2 ? cr2 : r2;
if (cost >= ans) continue;
if (cost < best[u][k]) {
best[u][k] = best[k][u] = cost;
pqPush(u < k ? u * n + k : k * n + u, cost);
}
if (cost < best[v][k]) {
best[v][k] = best[k][v] = cost;
pqPush(v < k ? v * n + k : k * n + v, cost);
}
}
for (int k : adj[v]) {
if (k == u || k == v) continue;
double cr2 = circumR2(u, v, k);
double cost = cr2 > r2 ? cr2 : r2;
if (cost >= ans) continue;
if (cost < best[u][k]) {
best[u][k] = best[k][u] = cost;
pqPush(u < k ? u * n + k : k * n + u, cost);
}
if (cost < best[v][k]) {
best[v][k] = best[k][v] = cost;
pqPush(v < k ? v * n + k : k * n + v, cost);
}
}
}
System.out.printf("%.10f%n", Math.sqrt(ans));
}
public static void main(String[] args) throws Exception {
new Thread(null, () -> {
try {
int t = ri();
while (t-- > 0) solve();
} catch (IOException e) { throw new RuntimeException(e); }
}, "m", 1 << 26).start();
}
}
cpp(30/30):
1. 【问题抽象】
本题核心是在点集中寻找一条从起点(0,1)到终点(包含n-1)的路径，使得路径上连续三点 * 构成的外接圆直径（或两点间距）的最大值达到最小。
状态定义：min_dist[u][v] 表示当前到达点对 (u, v) 时的最小代价平方 r^2。
2. 【几何策略与公式】
对于点 u, v 和新加入的点 k 构成的三角形，设边长平方分别为 a^2, b^2, c^2 (a为最长边)：
钝角/直角三角形 (b^2 + c^2 <= a^2):
外接圆直径由最长边决定，代价 cost = a^2 / 4。
锐角三角形 (b^2 + c^2 > a^2):
用外接圆半径公式 R^2 = (a^2 * b^2 * c^2) / (4*a^2*b^2 - (a^2+b^2-c^2)^2)。
代码中简化为：num = a^2 * b^2 * c^2, den = 4*b^2*c^2 - (b^2+c^2-a^2)^2。
3. 【核心优化技巧】
剪枝策略：
直径剪枝：若 d(u,k)^2 / 4 >= 当前已知最优解，则无需进行后续复杂的锐角代价计算。
对于特殊构造的稀疏图或长边，几何计算开销巨大。
方案：三角形 (u, v, k) 的最小覆盖圆半径 R 一定满足 。 如果边
本身的代价
已经超过了目标状态
当前已知的最优解，那么无论
在哪里，都无法通过当前操作优化
。
// 仅需一次乘法和比较，剪掉大量无效几何计算
if (distMat[u][k] * 0.25 >= min_dist[u][k]) skip_update_u = true;惰性除法：锐角三角形外接圆半径公式需要浮点除法，指令周期极长。
方案：利用不等式变形，将除法转换为乘法。
/*
* 核心优化思路:
* 1. 内存: 维护全对称 min_dist[N][N]，保证读取时均为 Stride-1 连续访问 。
* 2. 剪枝: 直径剪枝 (d^2/4 >= best)，过滤稀疏长边。
* 3. 运算: 惰性除法 (乘法代替除法判定)，Lambda 强制内联，循环拆分消除分支。
*/
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
#include <iomanip>
#include <cstring>
#include <cstdio>
using namespace std;
// === 快读 ===
const int BUF_SIZE = 1 << 18;
char buffer[BUF_SIZE];
int buf_ptr = BUF_SIZE, buf_len = 0;
inline int next_char() {
if (buf_ptr >= buf_len) {
buf_ptr = 0;
buf_len = fread(buffer, 1, BUF_SIZE, stdin);
if (buf_len == 0) return EOF;
}
return buffer[buf_ptr++];
}
inline bool scan_int(int &x) {
int c = next_char();
while (c != EOF && (c < '0' || c > '9')) c = next_char();
if (c == EOF) return false;
x = 0;
while (c >= '0' && c <= '9') { x = x * 10 + (c - '0'); c = next_char(); }
return true;
}
inline void scan_long(long long &x) {
int c = next_char();
while (c != EOF && (c < '0' || c > '9')) c = next_char();
x = 0;
while (c >= '0' && c <= '9') { x = x * 10 + (c - '0'); c = next_char(); }
}
const int MAXN = 1505;
const int MAX_ID = MAXN * MAXN + 7;
const double INF = 1e18;
long long px[MAXN], py[MAXN];
double distMat[MAXN][MAXN];
double min_dist[MAXN][MAXN]; // 对称存储
// 手写堆
int pq[MAX_ID], qp[MAX_ID], pqSize = 0;
double keys[MAX_ID];
inline bool greater_idx(int i, int j) { return keys[pq[i]] > keys[pq[j]]; }
inline void exch(int i, int j) {
int swap = pq[i]; pq[i] = pq[j]; pq[j] = swap;
qp[pq[i]] = i; qp[pq[j]] = j;
}
void swim(int k) { while (k > 1 && greater_idx(k >> 1, k)) { exch(k, k >> 1); k >>= 1; } }
void sink(int k) {
while ((k << 1) <= pqSize) {
int j = k << 1;
if (j < pqSize && greater_idx(j, j + 1)) j++;
if (!greater_idx(k, j)) break;
exch(k, j); k = j;
}
}
inline void push_or_update(int id, double cost) {
if (cost < keys[id]) {
keys[id] = cost;
if (qp[id] != -1) swim(qp[id]);
else { qp[id] = ++pqSize; pq[pqSize] = id; swim(pqSize); }
}
}
inline int del_min() {
int minId = pq[1]; exch(1, pqSize--); sink(1); qp[minId] = -1;
return minId;
}
void solve() {
int n;
if (!scan_int(n)) return;
for (int i = 0; i < n; i++) { scan_long(px[i]); scan_long(py[i]); }
if (n < 2) { printf("%.10f\n", 0.0); return; }
// 预处理距离 (double)
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
long long dx = px[i] - px[j], dy = py[i] - py[j];
double d2 = (double)(dx * dx + dy * dy);
distMat[i][j] = distMat[j][i] = d2;
}
}
// 初始化
for (int i = 0; i < n; i++) fill(min_dist[i], min_dist[i] + n, INF);
int limit = n * n;
fill(keys, keys + limit, INF);
fill(qp, qp + limit, -1);
pqSize = 0;
double start_cost = distMat[0][1] * 0.25;
min_dist[0][1] = start_cost; // 对称性暂不需要，因为只推一个
push_or_update(1, start_cost); // ID: 0*n+1
double ans = INF;
while (pqSize > 0) {
int uId = del_min();
double r2 = keys[uId];
if (r2 >= ans) continue;
int u = uId / n, v = uId % n;
if (r2 > min_dist[u][v]) continue; // 惰性删除
if (u == n - 1 || v == n - 1) { ans = r2; break; }
// 缓存指针
double* d_row_u = min_dist[u];
double* d_row_v = min_dist[v];
double* g_row_u = distMat[u];
double* g_row_v = distMat[v];
double val_d_uv = distMat[u][v];
// 核心更新逻辑
auto process = [&](int k, int id_u, int id_v) __attribute__((always_inline)) {
double best_u = d_row_u[k];
double best_v = d_row_v[k];
if (best_u <= r2 && best_v <= r2) return; // 基础剪枝
double d_uk = g_row_u[k];
double d_vk = g_row_v[k];
// 直径剪枝
if (d_uk * 0.25 >= best_u && d_vk * 0.25 >= best_v) return;
double cost, a2, b2, c2;
if (val_d_uv >= d_uk && val_d_uv >= d_vk) { a2 = val_d_uv; b2 = d_uk; c2 = d_vk; }
else if (d_uk >= val_d_uv && d_uk >= d_vk) { a2 = d_uk; b2 = val_d_uv; c2 = d_vk; }
else { a2 = d_vk; b2 = val_d_uv; c2 = d_uk; }
if (b2 + c2 <= a2) { // 钝角/直角
double geo = a2 * 0.25;
cost = (geo > r2) ? geo : r2;
} else { // 锐角 (惰性除法)
double limit = (best_u > best_v) ? best_u : best_v;
if (r2 > limit) cost = r2;
else {
double term = b2 + c2 - a2;
double den = 4.0 * b2 * c2 - term * term;
double num = a2 * b2 * c2;
if (num >= limit * den) cost = limit;
else {
cost = num / den;
if (cost < r2) cost = r2;
}
}
}
// 状态更新 (维护对称性)
// d_uk*0.25 >= best_u 已在上面判断过，此处只需 check cost
if (cost < best_u && !(d_uk * 0.25 >= best_u)) {
d_row_u[k] = cost; min_dist[k][u] = cost; push_or_update(id_u, cost);
}
if (cost < best_v && !(d_vk * 0.25 >= best_v)) {
d_row_v[k] = cost; min_dist[k][v] = cost; push_or_update(id_v, cost);
}
};
// 循环拆分 (无分支)
for (int k = 0; k < u; k++) process(k, k * n + u, k * n + v);
for (int k = u + 1; k < v; k++) process(k, u * n + k, k * n + v);
for (int k = v + 1; k < n; k++) process(k, u * n + k, v * n + k);
}
printf("%.10f\n", sqrt(ans));
}
int main() {
int t;
if (scan_int(t)) while (t--) solve();
return 0;
}
2026.02.15 更新优化版算法 通过Delaunay 三角剖分把每个状态的邻居从 O(n) 降到 O(deg≈6)，复杂度从 O(n³) 降到 O(n² log n)。
相关知识点：https://oi-wiki.org/geometry/triangulation/ （Delaunay 三角剖分）
/**
* L3-039 攀岩
*
* 算法: 边状态 Dijkstra (min-max path)
* 状态 (u,v) 表示两臂抓着 u 和 v
* 转移 (u,v)->(v,k): 代价 = max(当前, circumR^2(u,v,k))
*
* 关键优化: 对每个状态 (u,v), 只枚举 k ∈ Delaunay邻居(u) ∪ Delaunay邻居(v)
* 理由: Delaunay 三角剖分最小化外接圆, 最优的第三点一定是 Delaunay 邻居
* (或在以uv为直径的圆内, 此时 circumR=dist(u,v)/2 不增加代价)
*
* 额外: 对每个 (u,v), 还需考虑"以uv为直径的圆内的点"作为免费转移
* 这些点通过 Delaunay 邻居的邻居可以间接覆盖
*
* 复杂度: O(n^2 * deg * log(n^2)), deg ≈ 6
*/
#pragma GCC optimize("O3,unroll-loops")
#pragma GCC target("avx2,bmi,bmi2,popcnt")
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <cassert>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
// === 快读 ===
const int BUF = 1 << 18;
char buf[BUF]; int bp = BUF, bl = 0;
inline int gc() {
if (bp >= bl) { bp = 0; bl = fread(buf, 1, BUF, stdin); if (!bl) return EOF; }
return buf[bp++];
}
inline bool ri(int &x) {
int c = gc(); while (c != EOF && (c < '0' || c > '9')) c = gc();
if (c == EOF) return false;
x = 0; while (c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = gc(); }
return true;
}
inline void rl(ll &x) {
int c = gc(); while (c != EOF && (c < '0' || c > '9')) c = gc();
x = 0; while (c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = gc(); }
}
// === Delaunay 三角剖分 (Guibas-Stolfi, O(n log n)) ===
namespace Delaunay {
struct Pt {
ll x, y; int id;
Pt() {}
Pt(ll x, ll y, int id = -1) : x(x), y(y), id(id) {}
Pt operator-(const Pt& p) const { return {x - p.x, y - p.y}; }
ll cross(const Pt& p) const { return x * p.y - y * p.x; }
ll cross(const Pt& a, const Pt& b) const { return (a - *this).cross(b - *this); }
ll dot(const Pt& p) const { return x * p.x + y * p.y; }
ll sqr() const { return dot(*this); }
bool operator==(const Pt& p) const { return x == p.x && y == p.y; }
};
struct QE {
Pt org; QE *rot, *onext; bool used;
QE* rev() const { return rot->rot; }
QE* lnext() const { return rot->rev()->onext->rot; }
QE* oprev() const { return rot->onext->rot; }
Pt dest() const { return rev()->org; }
};
const int POOL = 2000000;
QE pool[POOL]; int pcnt;
void init() { pcnt = 0; }
QE* make_edge(Pt a, Pt b) {
QE *e1 = &pool[pcnt++], *e2 = &pool[pcnt++];
QE *e3 = &pool[pcnt++], *e4 = &pool[pcnt++];
e1->org = a; e2->org = b;
e3->org = e4->org = {(ll)1e18, (ll)1e18};
e1->rot = e3; e2->rot = e4; e3->rot = e2; e4->rot = e1;
e1->onext = e1; e2->onext = e2; e3->onext = e4; e4->onext = e3;
e1->used = e2->used = e3->used = e4->used = false;
return e1;
}
void splice(QE* a, QE* b) {
swap(a->onext->rot->onext, b->onext->rot->onext);
swap(a->onext, b->onext);
}
void del_edge(QE* e) {
splice(e, e->oprev());
splice(e->rev(), e->rev()->oprev());
}
QE* connect(QE* a, QE* b) {
QE* e = make_edge(a->dest(), b->org);
splice(e, a->lnext());
splice(e->rev(), b);
return e;
}
bool left_of(Pt p, QE* e) { return p.cross(e->org, e->dest()) > 0; }
bool right_of(Pt p, QE* e) { return p.cross(e->org, e->dest()) < 0; }
bool in_circle(Pt a, Pt b, Pt c, Pt d) {
__int128 A = a.sqr(), B = b.sqr(), C = c.sqr(), D = d.sqr();
__int128 det = 0;
det += (__int128)(a.x) * ((__int128)(b.y) * C - (__int128)(c.y) * B
- (__int128)(b.y) * D + (__int128)(d.y) * B
+ (__int128)(c.y) * D - (__int128)(d.y) * C);
det -= (__int128)(b.x) * ((__int128)(a.y) * C - (__int128)(c.y) * A
- (__int128)(a.y) * D + (__int128)(d.y) * A
+ (__int128)(c.y) * D - (__int128)(d.y) * C);
det += (__int128)(c.x) * ((__int128)(a.y) * B - (__int128)(b.y) * A
- (__int128)(a.y) * D + (__int128)(d.y) * A
+ (__int128)(b.y) * D - (__int128)(d.y) * B);
det -= (__int128)(d.x) * ((__int128)(a.y) * B - (__int128)(b.y) * A
- (__int128)(a.y) * C + (__int128)(c.y) * A
+ (__int128)(b.y) * C - (__int128)(c.y) * B);
return det > 0;
}
pair<QE*, QE*> build(int l, int r, vector<Pt>& p) {
if (r - l + 1 == 2) {
QE* e = make_edge(p[l], p[r]);
return {e, e->rev()};
}
if (r - l + 1 == 3) {
QE *a = make_edge(p[l], p[l+1]), *b = make_edge(p[l+1], p[r]);
splice(a->rev(), b);
int sg = (p[l].cross(p[l+1], p[r]) > 0) ? 1 : (p[l].cross(p[l+1], p[r]) < 0) ? -1 : 0;
if (sg == 0) return {a, b->rev()};
QE* c = connect(b, a);
return sg == 1 ? make_pair(a, b->rev()) : make_pair(c->rev(), c);
}
int mid = (l + r) / 2;
auto [ldo, ldi] = build(l, mid, p);
auto [rdi, rdo] = build(mid + 1, r, p);
while (true) {
if (left_of(rdi->org, ldi)) { ldi = ldi->lnext(); continue; }
if (right_of(ldi->org, rdi)) { rdi = rdi->rev()->onext; continue; }
break;
}
QE* basel = connect(rdi->rev(), ldi);
auto valid = [&](QE* e) { return right_of(e->dest(), basel); };
if (ldi->org == ldo->org) ldo = basel->rev();
if (rdi->org == rdo->org) rdo = basel;
while (true) {
QE* lc = basel->rev()->onext;
if (valid(lc))
while (in_circle(basel->dest(), basel->org, lc->dest(), lc->onext->dest()))
{ QE* t = lc->onext; del_edge(lc); lc = t; }
QE* rc = basel->oprev();
if (valid(rc))
while (in_circle(basel->dest(), basel->org, rc->dest(), rc->oprev()->dest()))
{ QE* t = rc->oprev(); del_edge(rc); rc = t; }
if (!valid(lc) && !valid(rc)) break;
if (!valid(lc) || (valid(rc) && in_circle(lc->dest(), lc->org, rc->org, rc->dest())))
basel = connect(rc, basel->rev());
else
basel = connect(basel->rev(), lc->rev());
}
return {ldo, rdo};
}
// 返回三角形列表 (id_a, id_b, id_c)
vector<array<int,3>> triangulate(vector<Pt>& pts) {
int n = pts.size();
if (n < 3) return {};
init();
vector<Pt> p = pts;
sort(p.begin(), p.end(), [](const Pt& a, const Pt& b) {
return a.x < b.x || (a.x == b.x && a.y < b.y);
});
auto [le, re] = build(0, n - 1, p);
// 遍历所有三角形
QE* e = le;
vector<QE*> edges = {e};
while (e->onext->dest().cross(e->dest(), e->org) < 0) e = e->onext;
vector<Pt> tri_pts;
auto add = [&]() {
QE* cur = e;
do {
cur->used = true;
tri_pts.push_back(cur->org);
edges.push_back(cur->rev());
cur = cur->lnext();
} while (cur != e);
};
add();
tri_pts.clear();
int idx = 0;
while (idx < (int)edges.size()) {
if (!(e = edges[idx++])->used) add();
}
vector<array<int,3>> res;
for (int i = 0; i < (int)tri_pts.size(); i += 3) {
res.push_back({tri_pts[i].id, tri_pts[i+1].id, tri_pts[i+2].id});
}
return res;
}
}
// === 主算法 ===
const int MAXN = 1505;
const double INF = 1e18;
ll px[MAXN], py[MAXN];
double d2[MAXN][MAXN]; // dist^2 矩阵
double best[MAXN][MAXN]; // best[u][v] = 到达边(u,v)的最小瓶颈 r^2
vector<int> adj[MAXN]; // Delaunay 邻居
// 手写堆 (索引堆)
const int MAXID = MAXN * MAXN;
int pq[MAXID + 1], qp[MAXID + 1], pqSz;
double key[MAXID + 1];
inline bool gt(int i, int j) { return key[pq[i]] > key[pq[j]]; }
inline void ex(int i, int j) { swap(pq[i], pq[j]); qp[pq[i]] = i; qp[pq[j]] = j; }
void swim(int k) { while (k > 1 && gt(k >> 1, k)) { ex(k, k >> 1); k >>= 1; } }
void sink(int k) {
while ((k << 1) <= pqSz) {
int j = k << 1;
if (j < pqSz && gt(j, j + 1)) j++;
if (!gt(k, j)) break;
ex(k, j); k = j;
}
}
inline void pq_push(int id, double c) {
if (c < key[id]) {
key[id] = c;
if (qp[id] != -1) swim(qp[id]);
else { qp[id] = ++pqSz; pq[pqSz] = id; swim(pqSz); }
}
}
inline int pq_pop() { int r = pq[1]; ex(1, pqSz--); sink(1); qp[r] = -1; return r; }
// 三点最小覆盖圆半径的平方
inline double circumR2(int u, int v, int k) {
double a2 = d2[u][v], b2 = d2[u][k], c2 = d2[v][k];
// 找最长边
double mx, m1, m2;
if (a2 >= b2 && a2 >= c2) { mx = a2; m1 = b2; m2 = c2; }
else if (b2 >= a2 && b2 >= c2) { mx = b2; m1 = a2; m2 = c2; }
else { mx = c2; m1 = a2; m2 = b2; }
if (m1 + m2 <= mx) return mx * 0.25; // 钝角/直角
// 锐角: R^2 = a^2*b^2*c^2 / (4*b^2*c^2 - (b^2+c^2-a^2)^2)
double t = m1 + m2 - mx;
double den = 4.0 * m1 * m2 - t * t;
return mx * m1 * m2 / den;
}
void solve() {
int n;
if (!ri(n)) return;
for (int i = 0; i < n; i++) { rl(px[i]); rl(py[i]); }
if (n < 3) {
if (n == 2) {
double dx = px[0] - px[1], dy = py[0] - py[1];
printf("%.10f\n", sqrt(dx * dx + dy * dy) * 0.5);
} else {
printf("%.10f\n", 0.0);
}
return;
}
// 预处理距离矩阵
for (int i = 0; i < n; i++) {
d2[i][i] = 0;
for (int j = i + 1; j < n; j++) {
ll dx = px[i] - px[j], dy = py[i] - py[j];
d2[i][j] = d2[j][i] = (double)(dx * dx + dy * dy);
}
}
// Delaunay 三角剖分
vector<Delaunay::Pt> pts(n);
for (int i = 0; i < n; i++) pts[i] = {px[i], py[i], i};
auto tris = Delaunay::triangulate(pts);
for (int i = 0; i < n; i++) adj[i].clear();
// 从三角形提取邻接表
for (auto& [a, b, c] : tris) {
adj[a].push_back(b); adj[a].push_back(c);
adj[b].push_back(a); adj[b].push_back(c);
adj[c].push_back(a); adj[c].push_back(b);
}
// 去重
for (int i = 0; i < n; i++) {
sort(adj[i].begin(), adj[i].end());
adj[i].erase(unique(adj[i].begin(), adj[i].end()), adj[i].end());
}
// 初始化
for (int i = 0; i < n; i++) fill(best[i], best[i] + n, INF);
int lim = n * n;
fill(key, key + lim, INF);
fill(qp, qp + lim, -1);
pqSz = 0;
double sc = d2[0][1] * 0.25;
best[0][1] = best[1][0] = sc;
pq_push(0 * n + 1, sc);
pq_push(1 * n + 0, sc);
double ans = INF;
while (pqSz > 0) {
int id = pq_pop();
double r2 = key[id];
if (r2 >= ans) continue;
int u = id / n, v = id % n;
if (r2 > best[u][v]) continue;
if (u == n - 1 || v == n - 1) { ans = r2; break; }
// 枚举第三个点 k: 只枚举 u 和 v 的 Delaunay 邻居
// 对于 u 的邻居 k: 转移到 (u,k) 和 (v,k)
// 对于 v 的邻居 k: 转移到 (u,k) 和 (v,k)
auto tryK = [&](int k) __attribute__((always_inline)) {
if (k == u || k == v) return;
double cr2 = circumR2(u, v, k);
double cost = cr2 > r2 ? cr2 : r2;
if (cost >= ans) return;
// 更新 (u,k)
if (cost < best[u][k]) {
best[u][k] = best[k][u] = cost;
int id1 = u < k ? u * n + k : k * n + u;
pq_push(id1, cost);
}
// 更新 (v,k)
if (cost < best[v][k]) {
best[v][k] = best[k][v] = cost;
int id2 = v < k ? v * n + k : k * n + v;
pq_push(id2, cost);
}
};
for (int k : adj[u]) tryK(k);
for (int k : adj[v]) tryK(k);
}
printf("%.10f\n", sqrt(ans));
}
int main() {
int t;
if (ri(t)) while (t--) solve();
return 0;
}
顺便 问一下 @Pretty Boy Fox 你盗我代码然后把博文收费是不是多少有点活不起了？
DAMO开发者矩阵，由阿里巴巴达摩院和中国互联网协会联合发起，致力于探讨最前沿的技术趋势与应用成果，搭建高质量的交流与分享平台，推动技术创新与产业应用链接，围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
22
0- 0
已为社区贡献1条内容
所有评论(0)