案例介绍： 

以下是使用监督学习来训练机器人避障：

在这个案例中，我们的目标是训练一个神经网络模型，使得机器人在持续运行的过程中不碰撞墙壁的条件下，到达几个指定点位，并且尽可能减少假阳性的观测数据。针对机器人碰撞/未碰撞墙壁，我们将使用神经网络来做出预测。

对此，我们使用pygame创建机器人避障的环境框架和渲染显示，使用pymunk为机器人设置物理引擎，比如运动控制参数，传感器观测参数。在机器人上设置前方5个方向的距离传感器，以及检查机器人碰撞产生的传感器来收集外部数据，再结合内部的转向控制参数就可以进行模型的训练了。

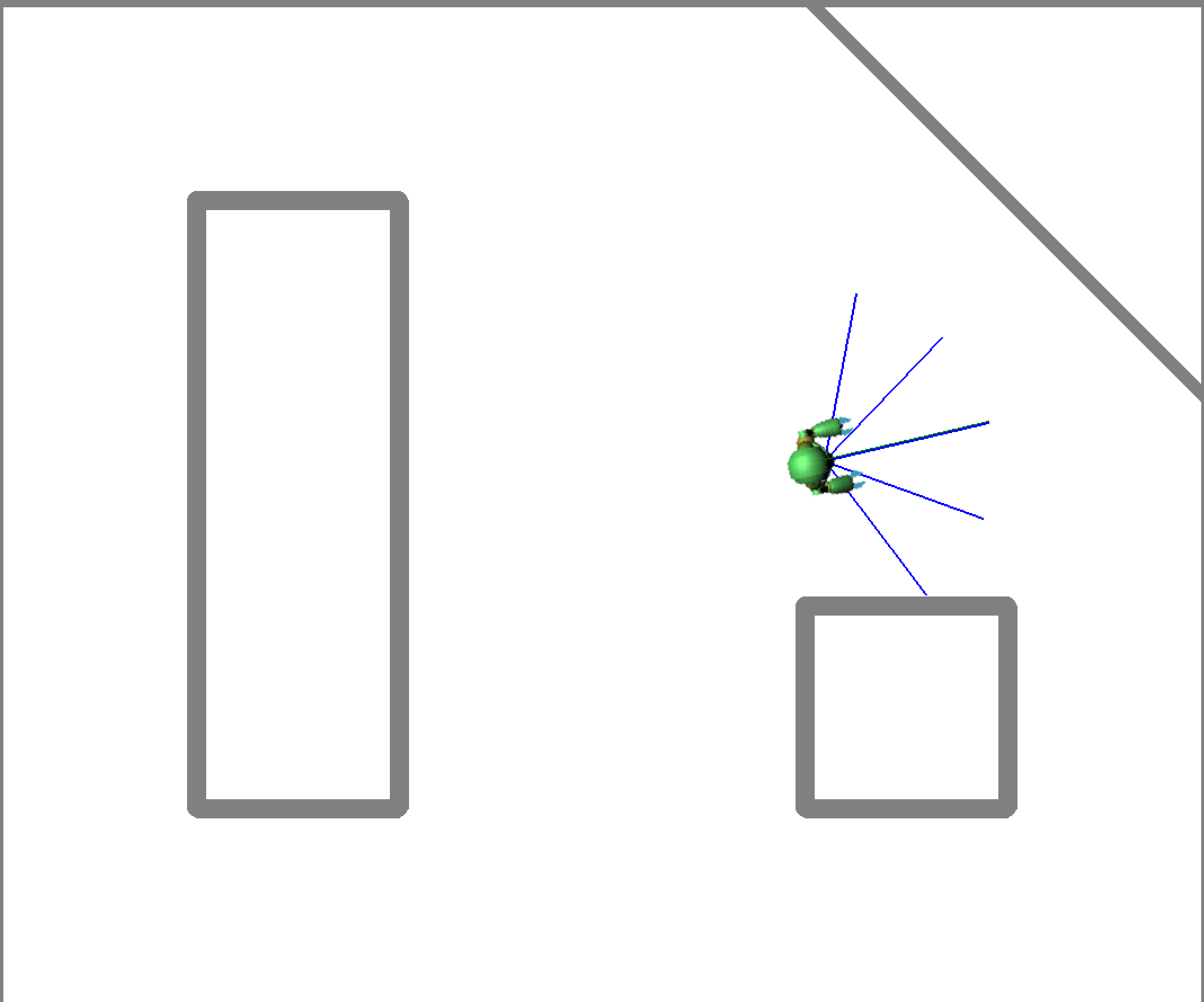
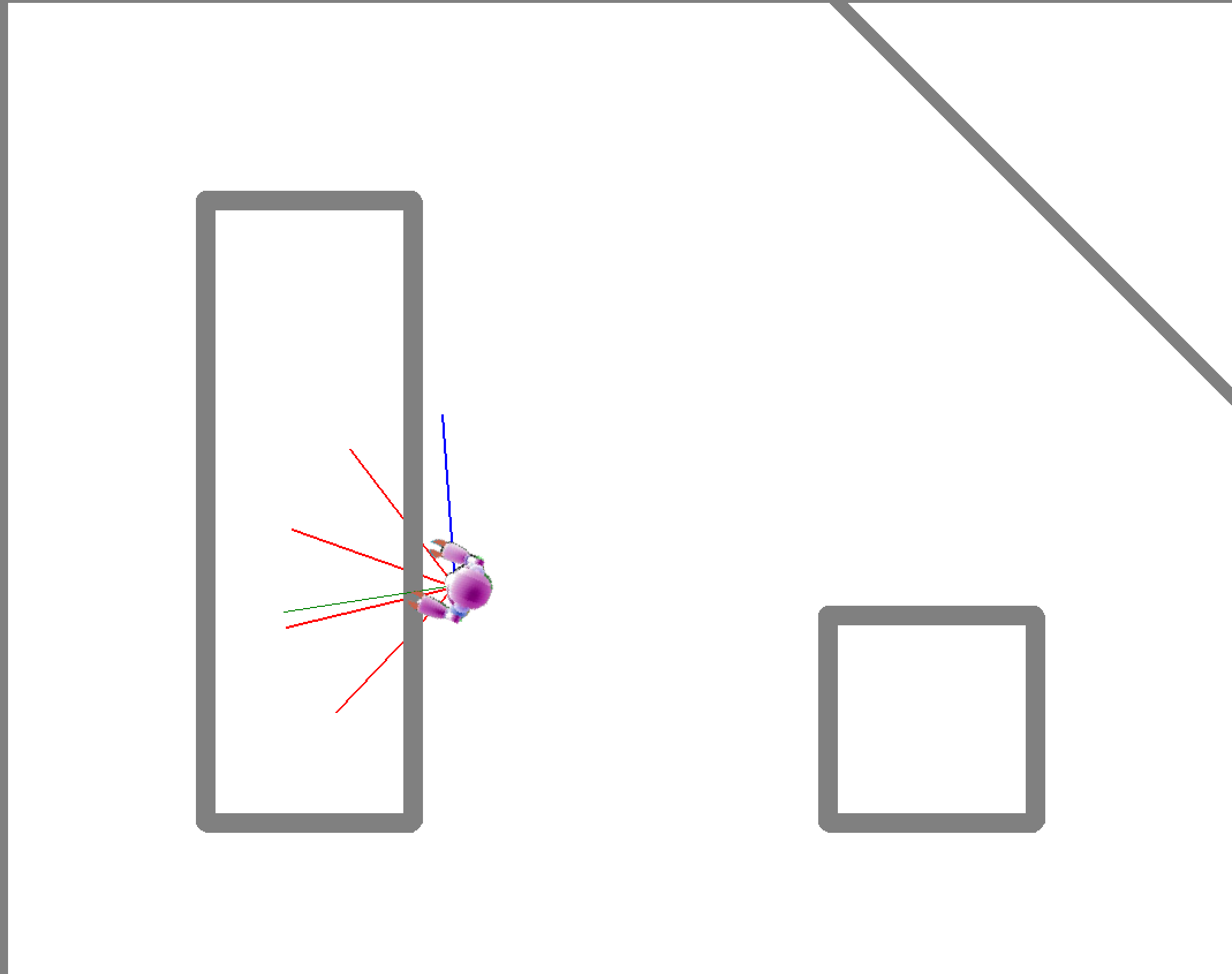
1. 收集数据：

训练之前，我们需要在当前的环境中收集数据。控制机器人进入walk模式，每隔0.5s记录一次数据，数据包含5个传感器的观测数据，1个动作数据和1个碰撞状态。在walk状态下，机器人撞墙会自动复位，方便自动收集数据。收集数据的时候，我们要尽可能地让机器人进入环境所有的状态下，并且记录这个状态会不会产生碰撞。

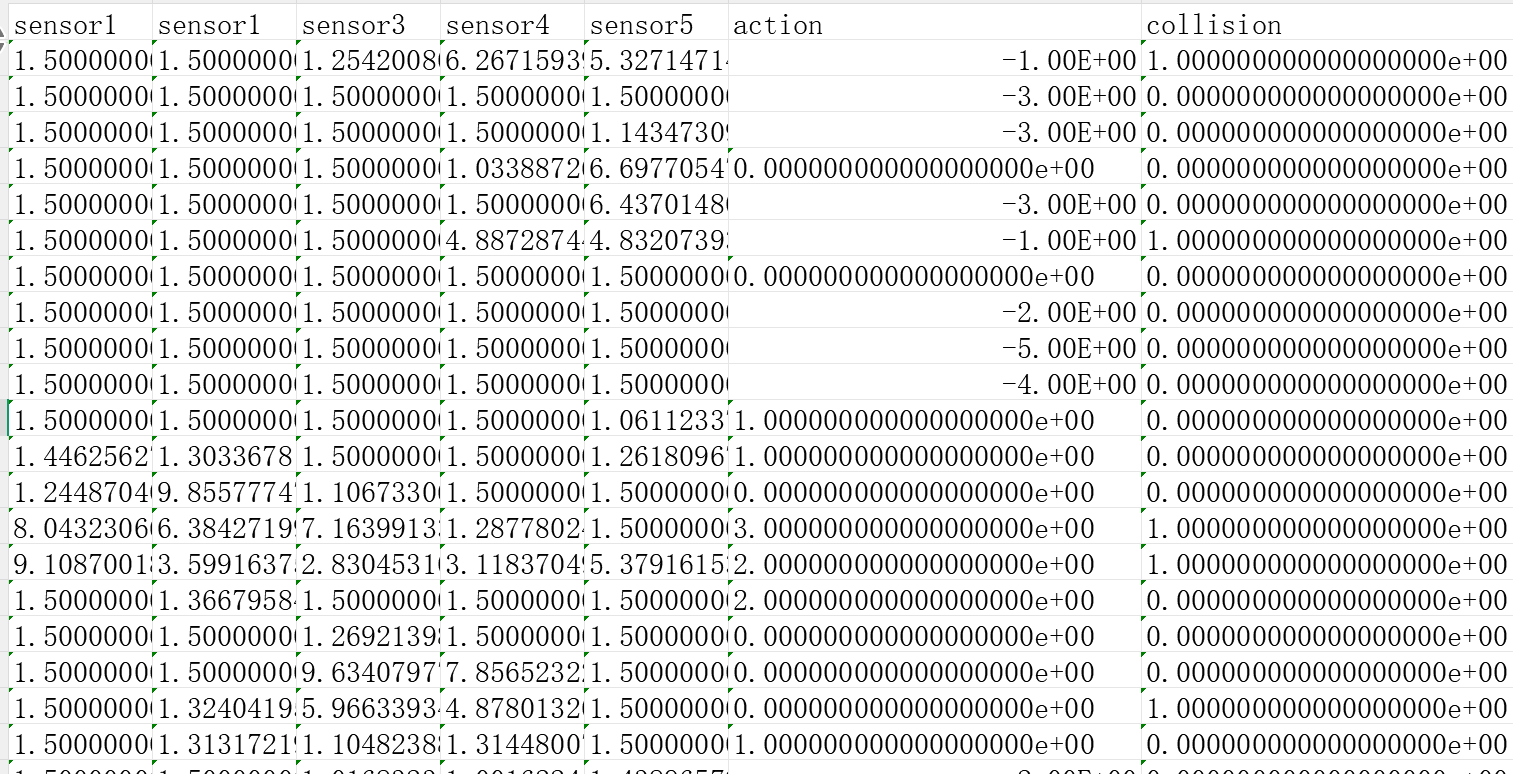
为提升碰撞检测模型的预测准确性与场景适配性，数据收集阶段需针对高风险场景与滞后碰撞场景进行标签优化：

（1）. 狭窄环境标签修正：狭窄区域的非碰撞数据本质是 “高概率碰撞的临界状态”，即使单次采样未发生碰撞，真实场景中动作微小偏差即可能引发碰撞。可根据项目需求，将此类高风险位置的非碰撞数据手动标注为碰撞标签，确保模型识别并预判临界风险。

（2）. 滞后碰撞标签追溯：拐角等场景中，碰撞可能由上一动作遗留风险导致（如机器人进入死角，无论向那个方向转向，都将发生碰撞。根本原因并非转向产生碰撞，而是进入死角导致的）。若仅将碰撞标签标注在转向动作上，模型会误判风险根源。需将碰撞标签追溯至引发风险的上一动作，避免因果错位。

2. 数据修剪：

模型预测的可信度通常会偏向数据比例多的一方。所以在收集完足够的数据之后，为了避免模型对碰撞数据预测可信度过低，要对数据进行剪枝平衡。

为什么模型预测的可信度会偏向数据比例多的一方？

因为模型训练的目标就是使总损失最小化。

假设有2000 个样本（200 碰撞 + 1800 不碰撞），有以下两种预测策略：

（1）所有样本的损失都是0.1，这样总损失就是200。

（2）1800个不碰撞的损失是0.08，200个碰撞损失是0.12，得到总损失是（1800×0.08）+（200×0.12）=144+24=168。

因为策略2总损失更小，模型最终会更倾向策略2。

如何进行数据修剪呢？

首先我们要考虑，取得的数据是有时序关系的。但是我们并不像让模型学习到数据中的时序关系。所以我们要打乱数据关系，为数据做混选。然后挑选出数据中较少的类别数据，也从另一类数据中挑选相同数量的数据，达到1：1的平衡（不一定1：1是最优的平衡策略，根据最终训练结果来调整）。

数据归一化？

从收集的数据来看每个sensor的样本特征和action的参数值所使用的量纲并不一样。我们希望模型能够平等的对待这些输入参数，因此要对输入参数进行归一化。在pytorch中可以使用self.scaler = MinMaxScaler(feature_range=(0, 1))将输入尺度缩放到（0，1）的范围上。

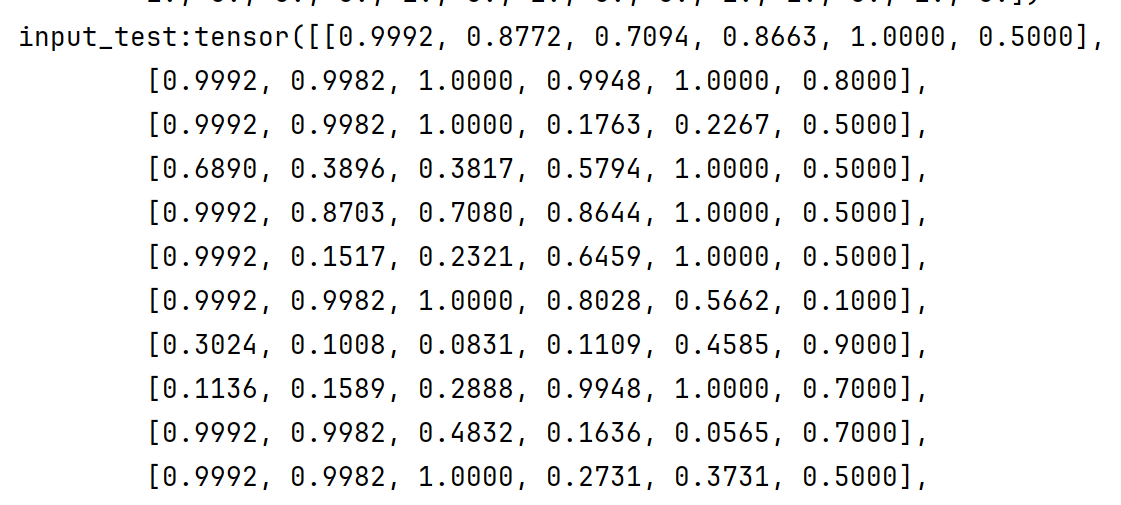
3. 模型选择：

碰撞预测显然是一个二分类的问题。而且对于样本点的分布很难用一条直线或者一个超平面来分割清楚。因此必须选择一个非线性模型来划分样本。激活函数可以用sigmoid或者relu，为模型增加非线性。

线性模型和非线性模型的区别？

举个例子，假设在二维平面上有一堆样本点。使用线性模型就是设计一条直线，让直线把分开样本点分成两类。而非线性模型就是设计一条曲线把样本点按类分开，而且隐藏层越多意味着曲线可以更自由更灵活，但是更容易受到噪声影响。

可参考：

【机器学习】线性（linear）与非线性（nonlinear）分类器区别_线性分类器和非线性分类器的区别-CSDN博客

选取哪种神经网络呢？PS：在其他文章会详细介绍各种网络模型。

FNN：做回归、分类典型任务的通用适配模型，像这种二分类的任务契合度比较高。

RNN：一般用来做时序依赖关系相关的预测。并不需要预测这种时序关系，相反我们还担心学习到这种时序关系影响泛化。

CNN：图像，网络输入时的常用预测模型。

LSTM：一般用来做长时间时序依赖关系相关的预测。

4. 网络构建

FNN包含输入层、隐藏层和输出层。

输入层：接受归一化的特征输入。通过权重和偏置与隐藏层相连。

隐藏层：通过权重和偏置形成隐藏层，隐藏层通过激活函数得到输出。

输出层：隐藏层的输出通过另一个激活函数得到分类概率。

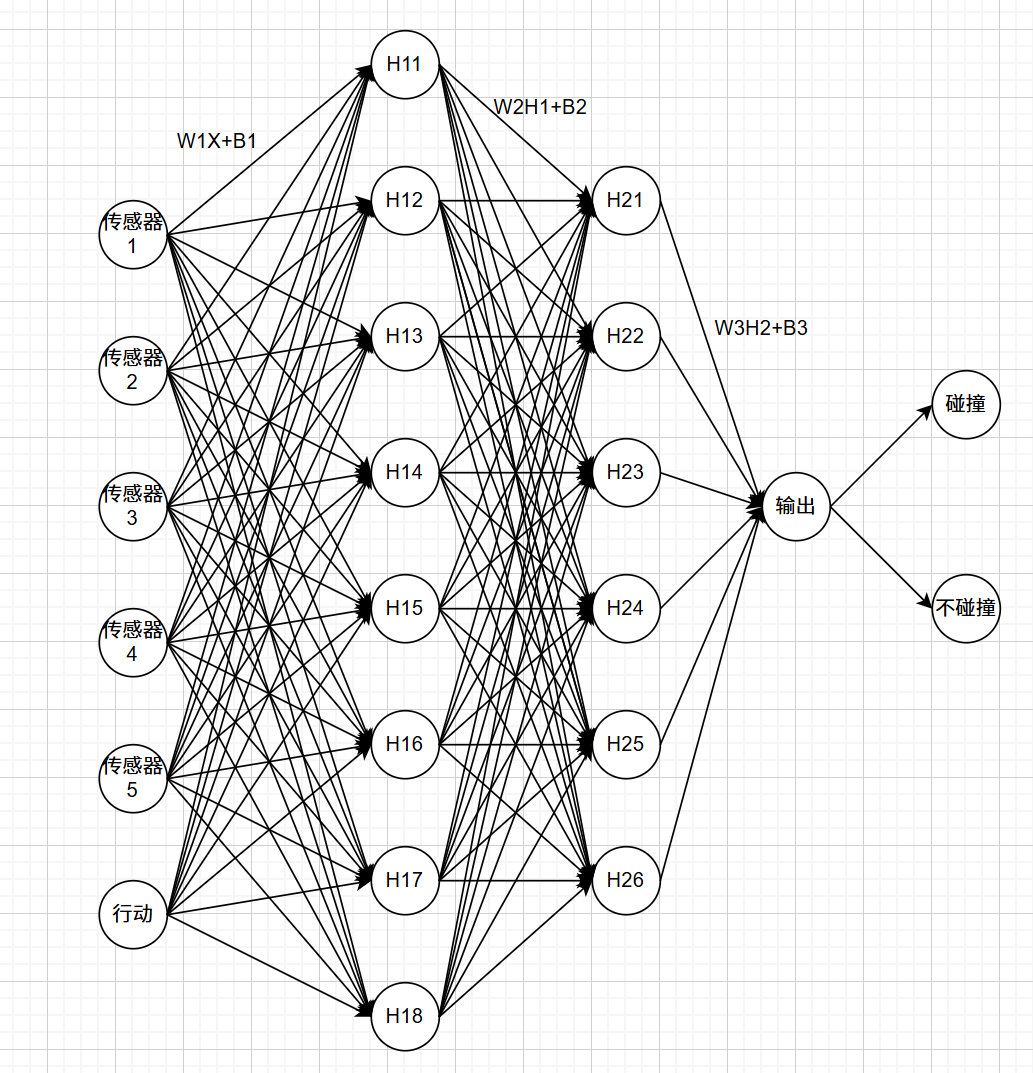
公式：

（1）.输入==》第一隐藏层

（2）.第一隐藏层==》第二隐藏层

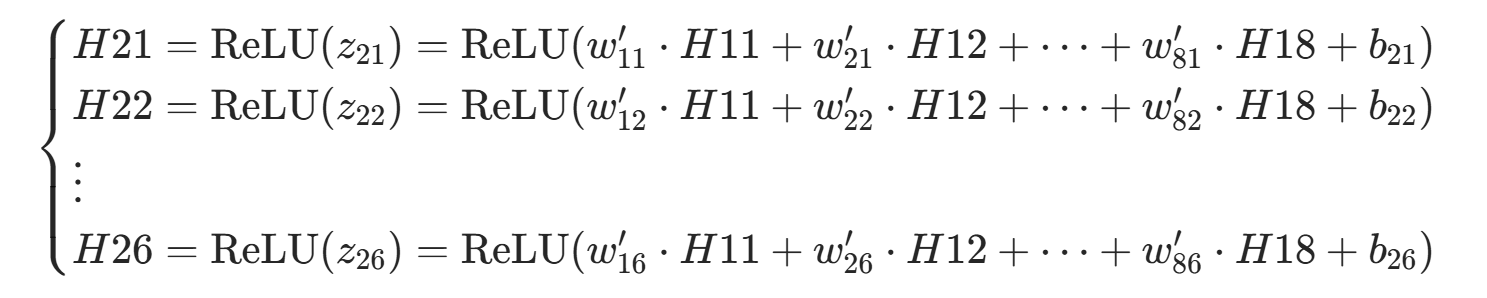
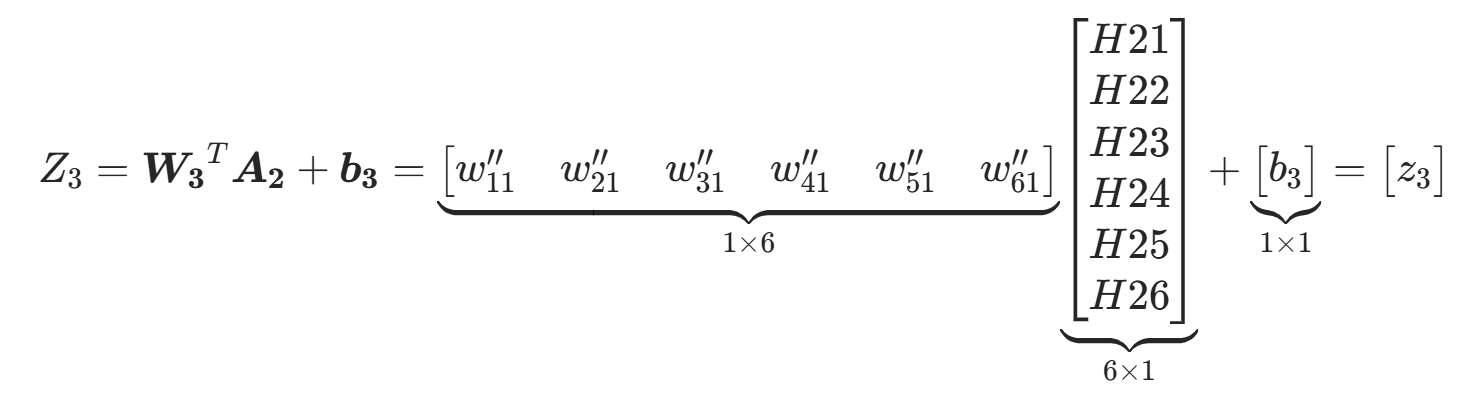
（3）.第二隐藏层==》输出
 

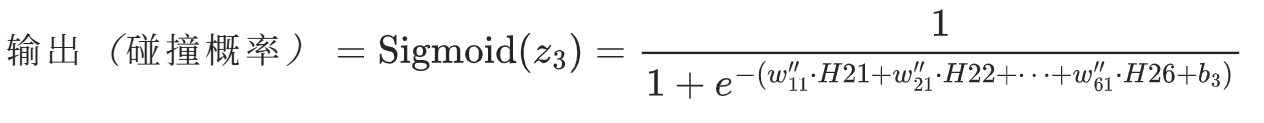
（4）.损失计算

BCELOSS：

MSELOSS：

二分类使用BCELOSS损失函数，MSELOSS函数适用回归任务。

举个例子：

假设在发生碰撞时（y=1），单次传播模型预估的碰撞概率为y^=0.8。

loss_sample=-(1*ln(0.8)+(1-1)*log(1-0.8))=0.22

假设在未发生碰撞时（y=0），单次传播模型预估的碰撞概率为y^=0.08。

loss_sample=-(0*ln(0.08)+(1-0)*log(1-0.08))=0.08

5. 训练

训练轮次通常根据经验判断。根据试错得出在800个训练轮次时会趋于稳定。通常选用32组样本作为一个训练批次，前向传播会得到32个碰撞预测结果。反向传播时，会先计算32组样本的损失以及反向传播梯度，然后各取平均，得到这一个批次的平均损失和平均反向传播梯度。最后使用 Adam 优化器，基于平均梯度对隐藏层 / 输出层权重进行统一更新，这样并行计算32组样本，可以大大减少训练时间，避免梯度震荡。

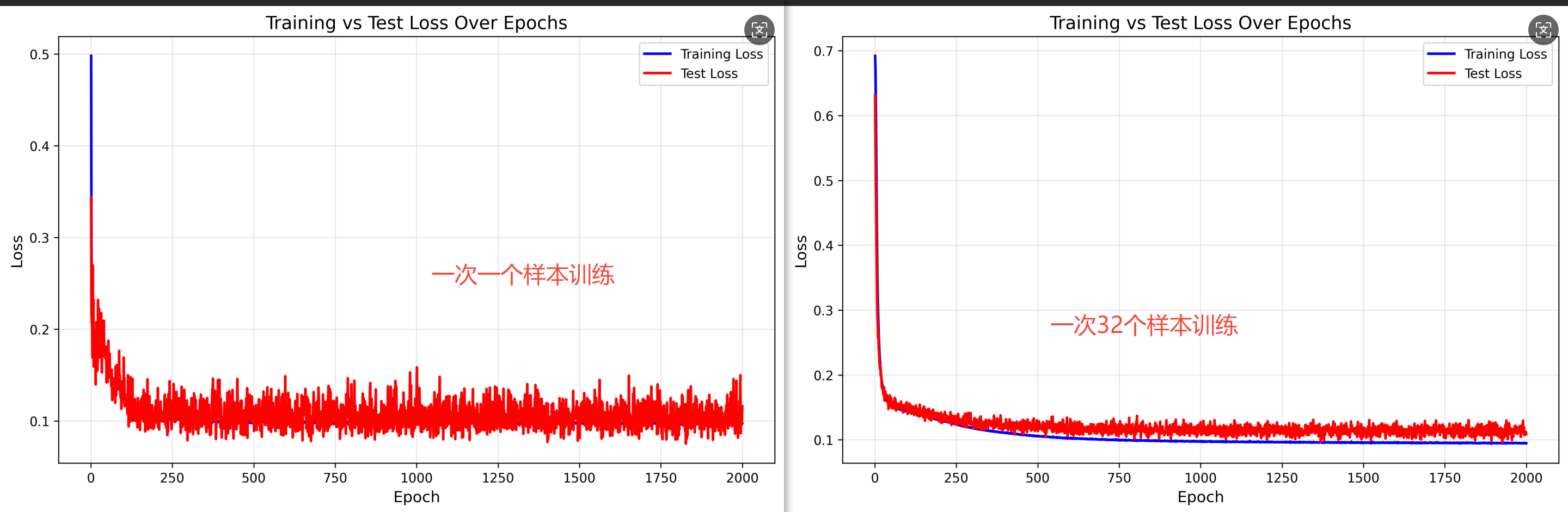
对于过拟合问题，通常使用正则化和丢弃法来规避，下面是基于碰撞预测项目，对正则化，丢弃法效果对预测效果的对比：

实验组合	最佳 F1 分数（综合过检漏检）
无丢弃无正则	0.8631
无丢弃有正则	0.8943
有丢弃无正则	0.8959
有丢弃有正则	0.9055

综合来看，增加丢弃、正则措施确实会提升模型的泛化能力。

6. 训练结果

隐藏层层数结果对比：

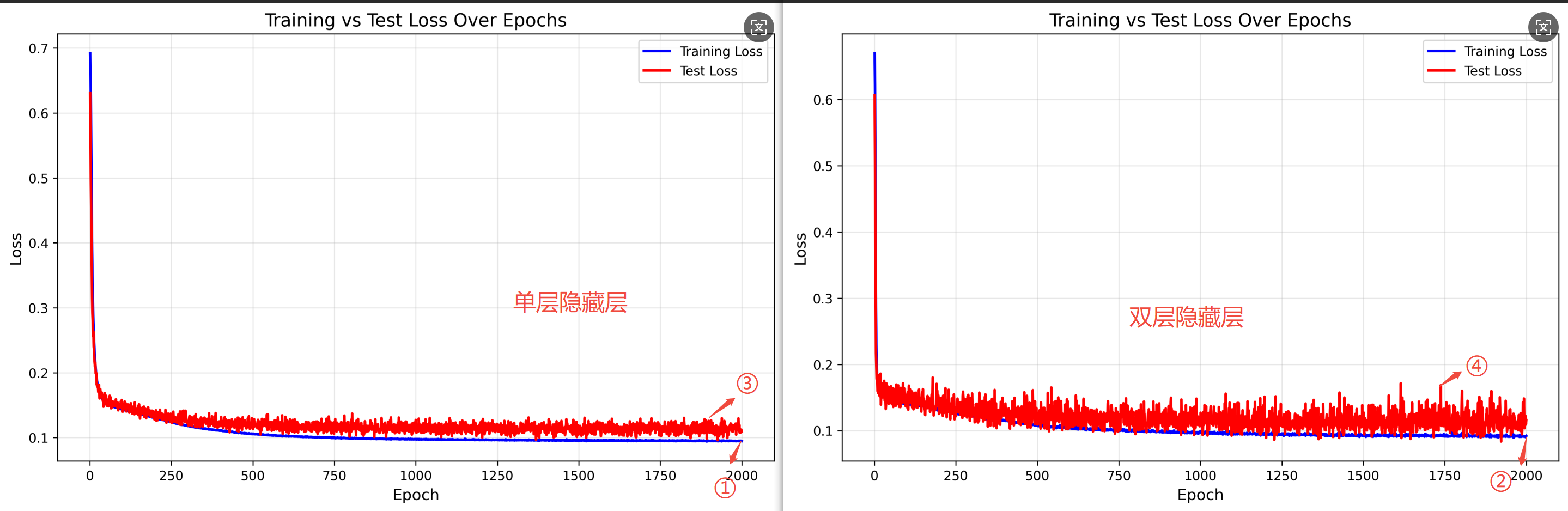
①vs②：双层隐藏层的训练损失更低。

③vs④：双层隐藏层的测试损失波动更大，泛化能力更弱。

一层隐藏层训练四次结果：

{"fractionalScore": 0.780000, "feedback": "False Positives: 20/1000  Missed Collisions 4/1000"}

{"fractionalScore": 0.970000, "feedback": "False Positives: 4/1000  Missed Collisions 1/1000"}

{"fractionalScore": 0.970000, "feedback": "False Positives: 9/1000  Missed Collisions 1/1000"}

{"fractionalScore": 0.940000, "feedback": "False Positives: 9/1000  Missed Collisions 2/1000"}

两层隐藏层训练四次结果：

{"fractionalScore": 0.930000, "feedback": "False Positives: 17/1000  Missed Collisions 0/1000"}

{"fractionalScore": 1.000000, "feedback": "False Positives: 7/1000  Missed Collisions 0/1000"}

{"fractionalScore": 0.930000, "feedback": "False Positives: 11/1000  Missed Collisions 2/1000"}

{"fractionalScore": 0.800000, "feedback": "False Positives: 21/1000  Missed Collisions 3/1000"}