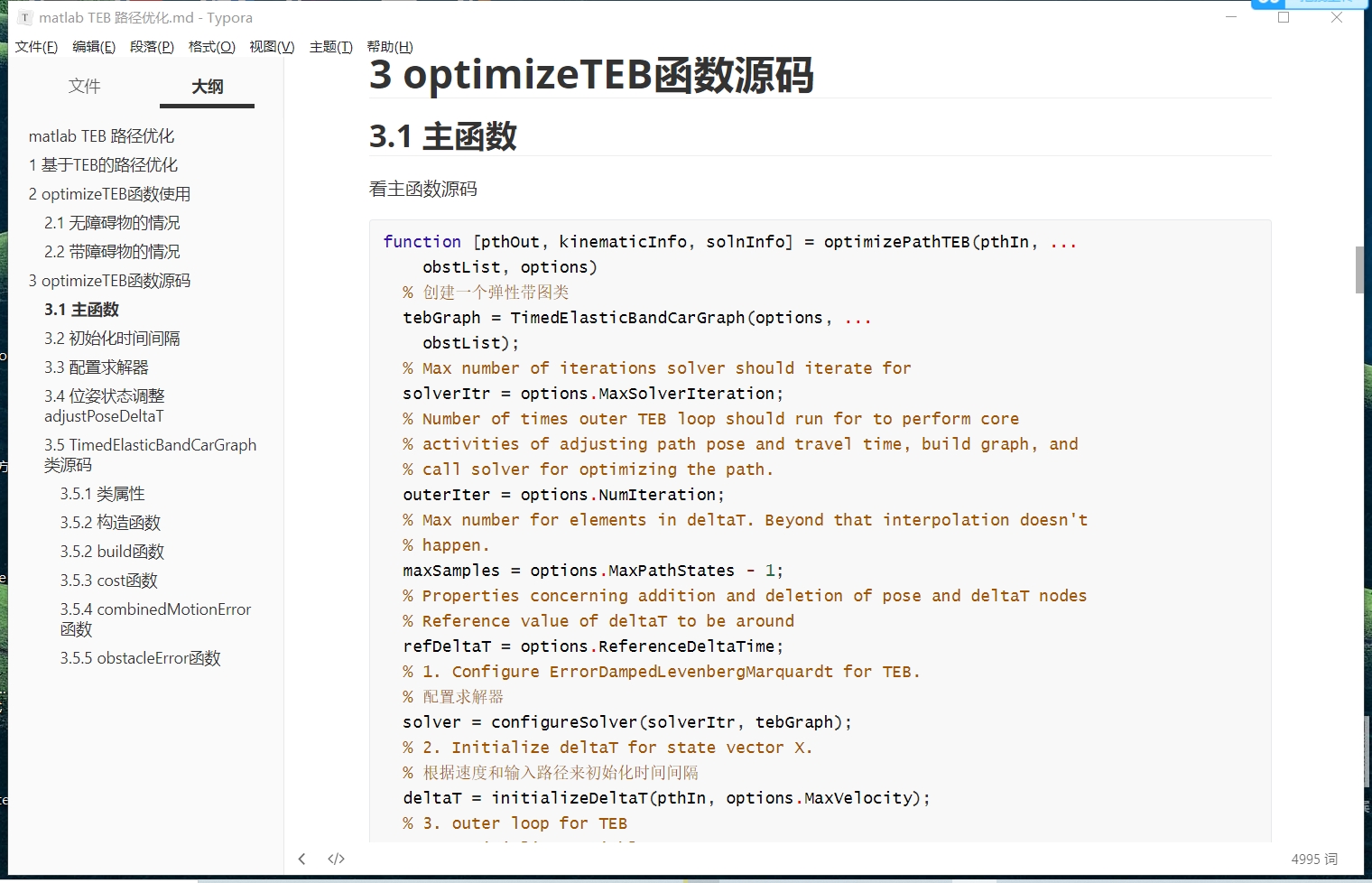
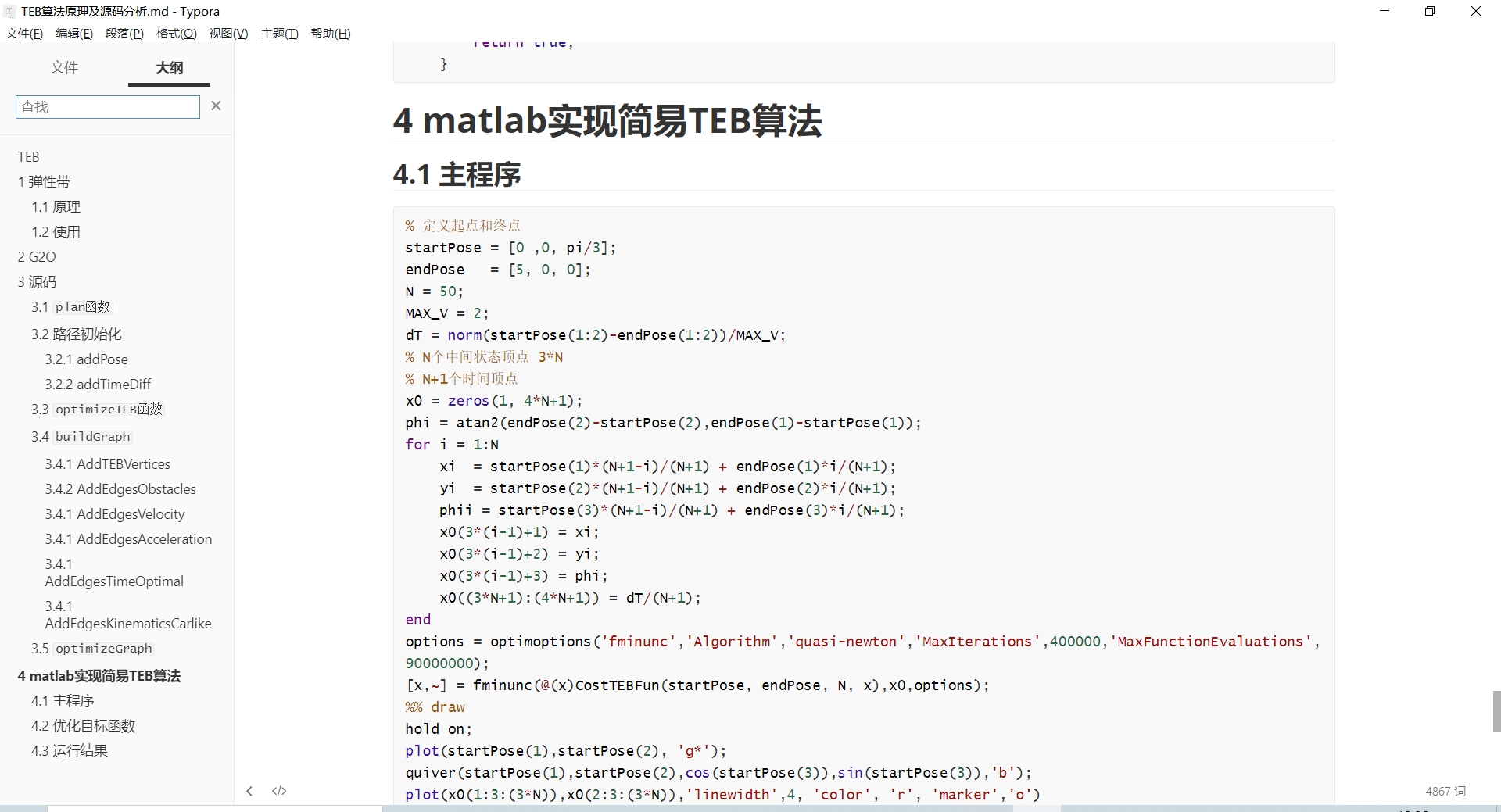
TEB算法原理与代码分析 详细文档+代码分析+matlab程序包 这段代码看起来是一个路径规划算法的实现。它使用了优化算法来寻找从起点到终点的最优路径，考虑了速度约束、运动学约束和障碍物避障。 首先，代码定义了起点和终点的位置，以及障碍物的位置（如果有）。然后，它设置了一些参数，如路径中的中间状态顶点数量N、最大速度MAX_V和时间步长dT。 接下来，代码初始化了一个状态向量x0，用于存储路径规划的初始解。它根据起点和终点的位置，以及N的数量，计算了中间状态顶点的位置和朝向，并将它们存储在x0中。同时，它还计算了每个状态顶点之间的时间间隔dT，并将其存储在x0中。 然后，代码使用优化算法（fminunc函数）来最小化一个成本函数（CostTEBFun函数）。这个成本函数考虑了时间最小约束、速度约束、运动学约束和障碍物避障。优化算法将调整状态向量x0的值，以找到使成本函数最小化的最优解x。 最后，代码绘制了路径规划的结果。它使用plot函数绘制了起点、中间状态顶点和终点的位置，使用quiver函数绘制了起点和中间状态顶点的朝向。如果有障碍物，它还使用plot函数绘制了障碍物的位置。 总结一下，这段代码实现了一个路径规划算法，用于寻找从起点到终点的最优路径。它考虑了速度约束、运动学约束和障碍物避障，并使用优化算法来搜索最优解。这个算法可以应用于机器人导航、自动驾驶等领域，解决路径规划问题。它涉及到的知识点包括优化算法、几何计算和路径规划算法。

一、TEB算法概述

Timed Elastic Band（时间弹性带，TEB）路径优化算法是一种面向移动机器人的轨迹优化技术，核心思想是将机器人路径视为一条“弹性带”，通过动态调整路径上的位姿节点与时间间隔，在满足机器人运动学约束（如最小转弯半径、速度/加速度限制）和环境约束（如障碍物规避）的前提下，实现路径的平滑性与时间最优性。

与传统路径规划算法（如A*、Dijkstra）相比，TEB算法不仅关注路径的几何可行性，还融入了时间维度，能够直接输出符合机器人动力学特性的运动轨迹，适用于无人车、AGV、移动机器人等需要精确运动控制的场景。在MATLAB环境中，TEB算法通过optimizePath与optimizeTEB函数实现，支持从参考路径生成到轨迹优化的全流程操作。

二、核心功能模块

MATLAB中的TEB路径优化功能由两大核心函数驱动，配合地图处理、约束配置、结果可视化等辅助模块，形成完整的轨迹优化流程。以下从功能角度拆解各核心模块的作用与交互逻辑。

2.1 参考路径生成模块

在进行TEB优化前，需先获取一条初始参考路径（通常由全局路径规划算法生成，如Hybrid A*）。该模块的核心功能是基于地图数据与起点/终点位姿，生成符合环境边界的初始路径，为后续优化提供基础。

关键功能点：

1. 地图加载与解析：读取二进制占据地图（如parkingMap.mat），通过binaryOccupancyMap函数转换为机器人可识别的栅格地图，并配置地图分辨率（如3米/栅格），确保环境障碍物信息的精准映射。
2. 运动学约束初始化：通过validatorOccupancyMap设置状态空间（SE2，即平面位置+航向角）与障碍物验证规则，例如设置路径节点间的验证距离（如0.1米），避免路径穿过障碍物。
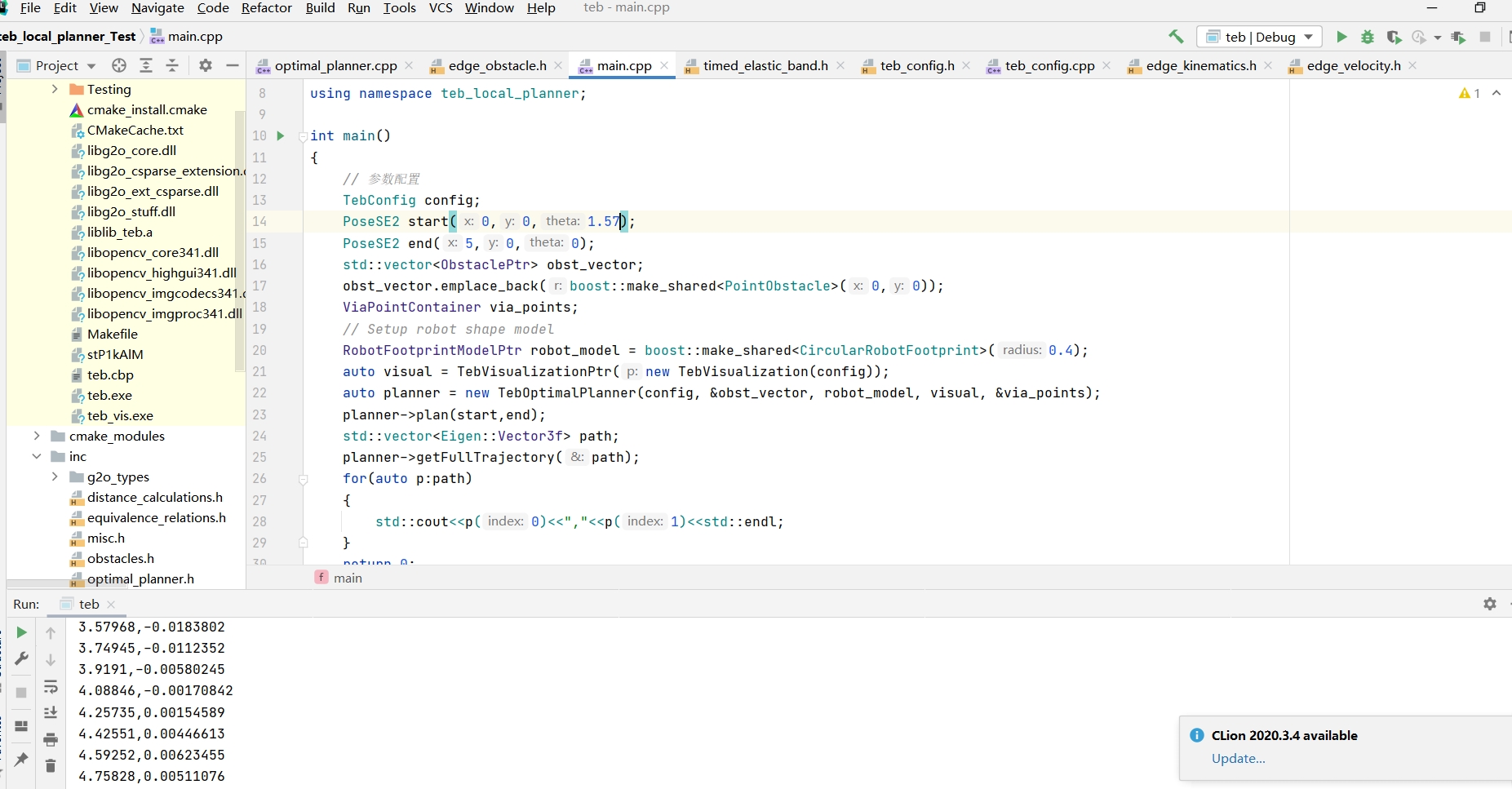
3. 全局路径规划：使用plannerHybridAStar（混合A*规划器）生成参考路径，配置机器人最小转弯半径（如3米）、运动基元长度（如4米）等参数，确保初始路径满足机器人基本运动学特性。

模块输出：

• 参考路径的位姿序列（包含x坐标、y坐标、航向角），存储于refPath.States中，作为TEB优化的输入。

2.2 TEB轨迹优化模块

该模块是TEB算法的核心，通过optimizePath函数封装，内部调用optimizeTEB实现具体优化逻辑。核心功能是对初始参考路径进行“弹性调整”，在满足多维度约束的同时，优化路径的平滑性与时间效率。

2.2.1 优化参数配置

在优化前需通过optimizePathOptions配置约束条件与优化目标权重，参数可分为运动学约束、时间约束、障碍物约束与优化目标权重四类，具体功能如下：

参数类别	关键参数	功能描述
运动学约束	MinTurningRadius	限制机器人最小转弯半径（如3米），避免路径出现无法实现的急转弯

| | MaxVelocity/MaxAcceleration | 限制最大线速度（如5 m/s）与最大线加速度（如1 m/s²），确保轨迹可执行 |

| 时间约束 | ReferenceDeltaTime | 参考时间间隔（如0.1秒），用于初始化路径节点间的时间差 |

| | MaxPathStates | 最大路径节点数，通过refPath.pathLength与节点间距（如0.2米）计算，控制优化精度与效率 |

| 障碍物约束 | ObstacleSafetyMargin | 障碍物安全距离（如2米），确保优化后路径与障碍物保持安全距离 |

TEB算法原理与代码分析 详细文档+代码分析+matlab程序包 这段代码看起来是一个路径规划算法的实现。它使用了优化算法来寻找从起点到终点的最优路径，考虑了速度约束、运动学约束和障碍物避障。 首先，代码定义了起点和终点的位置，以及障碍物的位置（如果有）。然后，它设置了一些参数，如路径中的中间状态顶点数量N、最大速度MAX_V和时间步长dT。 接下来，代码初始化了一个状态向量x0，用于存储路径规划的初始解。它根据起点和终点的位置，以及N的数量，计算了中间状态顶点的位置和朝向，并将它们存储在x0中。同时，它还计算了每个状态顶点之间的时间间隔dT，并将其存储在x0中。 然后，代码使用优化算法（fminunc函数）来最小化一个成本函数（CostTEBFun函数）。这个成本函数考虑了时间最小约束、速度约束、运动学约束和障碍物避障。优化算法将调整状态向量x0的值，以找到使成本函数最小化的最优解x。 最后，代码绘制了路径规划的结果。它使用plot函数绘制了起点、中间状态顶点和终点的位置，使用quiver函数绘制了起点和中间状态顶点的朝向。如果有障碍物，它还使用plot函数绘制了障碍物的位置。 总结一下，这段代码实现了一个路径规划算法，用于寻找从起点到终点的最优路径。它考虑了速度约束、运动学约束和障碍物避障，并使用优化算法来搜索最优解。这个算法可以应用于机器人导航、自动驾驶等领域，解决路径规划问题。它涉及到的知识点包括优化算法、几何计算和路径规划算法。

| | ObstacleCutOffDistance | 障碍物影响 cutoff 距离（如2.5米），超出该距离的障碍物不参与约束计算，减少计算量 |

| 优化目标权重 | WeightSmoothness/WeightTime | 平滑性权重（如1000）、时间权重（如10），调整不同优化目标的优先级 |

| | WeightObstacles | 障碍物权重（如50），权重越高，路径越倾向于远离障碍物 |

2.2.2 核心优化逻辑

optimizeTEB函数是优化模块的核心，通过“外层迭代调整节点+内层求解器优化”的双层逻辑，实现轨迹的动态优化，具体功能流程如下：

1. 时间间隔初始化：基于初始路径节点间的距离与最大速度，计算每个节点间的初始时间差（deltaT = 距离 / 最大速度），确保初始时间配置符合速度约束。
2. 路径节点动态调整：通过adjustPoseDeltaT函数，根据参考时间间隔（ReferenceDeltaTime）动态增删路径节点：
   - 若节点间时间差大于1.1倍参考值，插入新节点拆分时间差，提升路径精度；
   - 若节点间时间差小于0.9倍参考值，合并相邻节点，减少计算量；
   - 确保节点总数不超过MaxPathStates，平衡优化精度与效率。
3. 优化图构建：创建TimedElasticBandCarGraph（时间弹性带图），将路径节点（位姿）与时间节点（deltaT）作为图的顶点，同时构建多类型约束边，包括：
   - 运动学约束边：如非完整运动约束（确保机器人运动方向与路径一致）、最小转弯半径约束（避免超小半径转弯）；
   - 动力学约束边：如速度约束（节点间速度不超过最大值）、加速度约束（相邻节点间加速度不超过最大值）；
   - 障碍物约束边：基于障碍物位置与安全距离，构建路径节点与障碍物的距离约束，避免碰撞；
   - 时间优化边：最小化总时间，通过调整deltaT实现时间最优。
4. 非线性优化求解：使用Levenberg-Marquardt（LM）求解器（ErrorDampedLevenbergMarquardt），对构建的优化图进行求解。通过迭代最小化“约束误差加权和”（如平滑性误差、障碍物距离误差、时间误差），输出优化后的路径节点与时间序列。

模块输出：

• 优化后的路径位姿序列（optimizedPath）：包含调整后的x、y坐标与航向角，满足所有约束条件；
• 动力学信息（kineticInfo）：包含每个节点的时间戳、线速度、角速度，可直接用于机器人运动控制；
• 求解信息（solnInfo）：包含优化代价、迭代次数、约束误差，用于评估优化效果。

2.3 结果可视化与验证模块

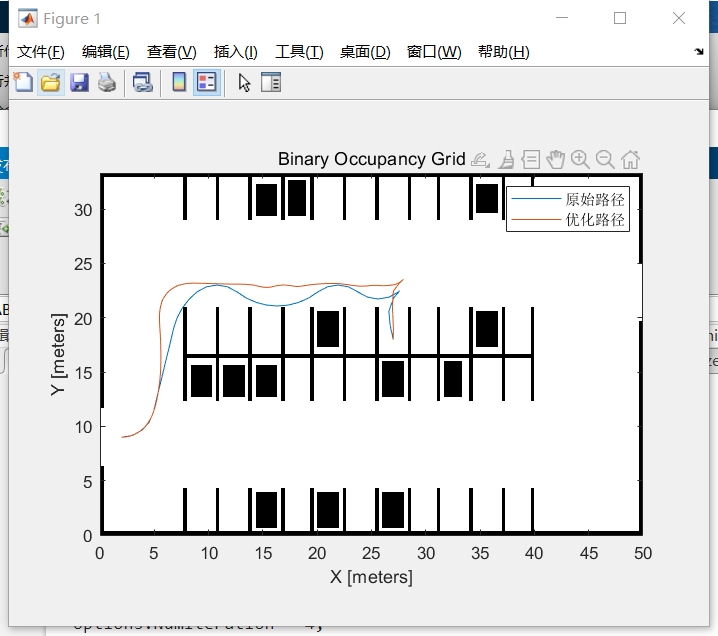
该模块的核心功能是直观展示初始路径与优化路径的差异，验证优化效果是否符合预期，同时支持障碍物与路径的叠加显示，确保路径安全性。

关键功能点：

1. 地图与路径绘制：通过show(map)显示栅格地图，使用plot函数分别绘制初始路径（如红色标记）与优化路径（如蓝色标记），直观对比路径平滑性提升效果。
2. 障碍物标记：在带障碍物场景中，通过plot(obstList(:,1), obstList(:,2), 'ko')标记障碍物位置（黑色圆点），验证优化路径是否避开障碍物。
3. 动力学信息可视化：可基于kineticInfo绘制速度-时间曲线、加速度-时间曲线，验证优化后的轨迹是否满足动力学约束（如速度未超过最大值）。

三、典型应用场景与效果

MATLAB中的TEB算法可适配无障碍物与有障碍物两类场景，不同场景下的优化目标与效果存在差异，具体如下：

3.1 无障碍物场景

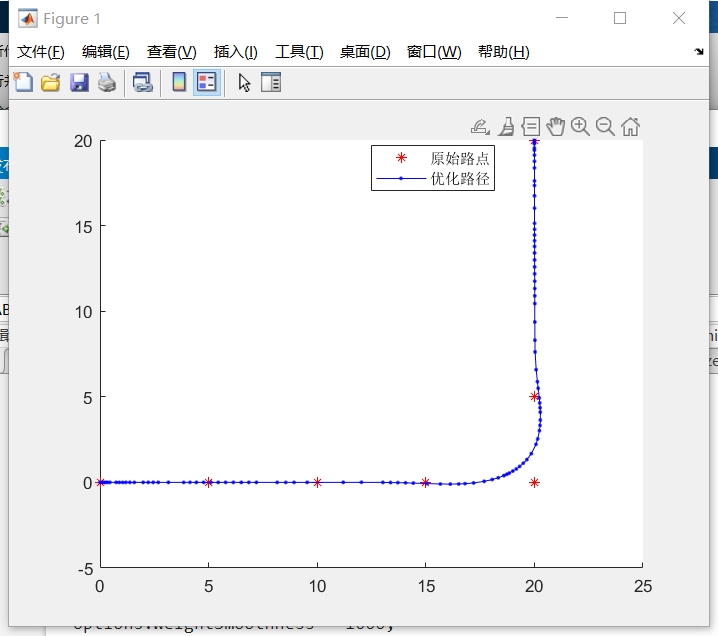
应用场景：开阔环境（如空旷停车场），核心优化目标是路径平滑性与时间最优性。

优化效果：

• 初始路径可能存在折线或突变（如直角转弯），优化后路径变为连续平滑的曲线，符合机器人运动学特性；
• 时间间隔（deltaT）被优化为均匀分布，确保速度稳定，避免频繁加减速；
• 例如，初始路径为“直线+直角转弯”，优化后转变为“平滑圆弧转弯”，转弯半径等于或大于MinTurningRadius，同时总时间缩短（如从5秒优化至4.2秒）。

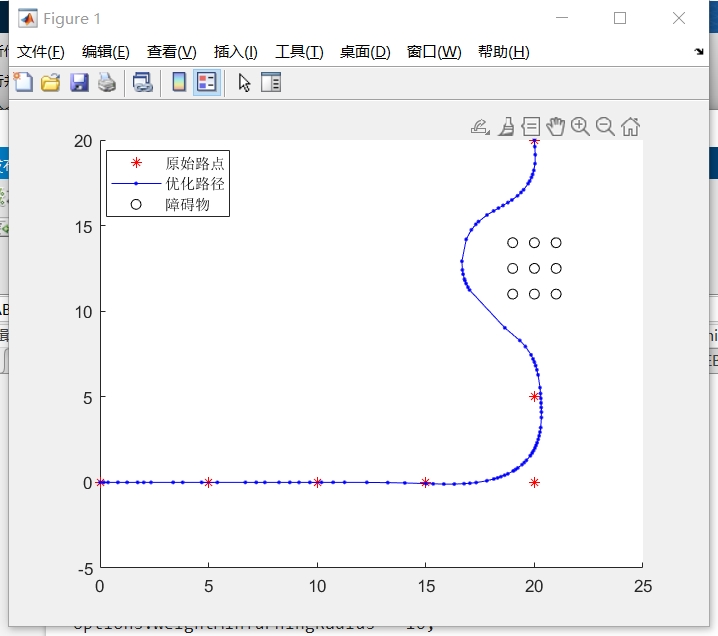
3.2 有障碍物场景

应用场景：复杂环境（如多障碍物车间），核心优化目标是障碍物规避与路径安全性。

优化效果：

• 优化算法通过调整路径节点位置，使路径与障碍物保持ObstacleSafetyMargin（如2米）以上的距离，避免碰撞；
• 当障碍物权重（WeightObstacles）提高（如从50调整至2000）时，路径会更显著地远离障碍物，优先级高于时间优化；
• 例如，初始路径靠近障碍物（距离0.5米），优化后路径偏移至距离障碍物2.5米处，同时保持路径平滑，未出现急转弯或速度突变。

四、核心函数调用关系与流程

MATLAB中TEB算法的函数调用关系呈分层结构，从顶层用户接口到底层优化逻辑，各函数职责明确，流程如下：

1. 用户接口层：optimizePath是用户直接调用的函数，负责参数验证（如输入路径维度、地图合法性）、地图障碍物转换（将栅格地图转换为障碍物列表）、优化参数传递，屏蔽底层实现细节。
2. 核心优化层：optimizeTEB是优化逻辑的核心，负责路径节点调整、优化图构建、LM求解器调用，实现“节点调整-图构建-求解”的迭代循环，直至满足迭代次数（NumIteration）或收敛条件。
3. 数据结构层：TimedElasticBandCarGraph是优化图的核心数据结构，封装了路径节点、时间节点、约束边、权重矩阵等信息，支持约束误差计算（cost函数）、雅可比矩阵计算（gradient函数），为求解器提供数据支持。

调用流程示意图：

用户配置参数 → optimizePath（参数验证、地图转换） → optimizeTEB（节点调整、图构建） → LM求解器（约束优化） → 输出优化结果

五、技术优势与适用范围

5.1 技术优势

1. 多约束融合：同时考虑运动学（转弯半径）、动力学（速度/加速度）、环境（障碍物）三类约束，生成的轨迹可直接用于机器人控制，无需二次处理；
2. 动态节点调整：通过增删路径节点，平衡优化精度与计算效率，避免节点过多导致的计算量激增，或节点过少导致的精度不足；
3. 权重可配置：支持通过调整目标权重（如平滑性、时间、障碍物），适配不同应用需求（如竞速场景可提高时间权重，安全场景可提高障碍物权重）；
4. MATLAB生态适配：可与MATLAB Robotics Toolbox中的其他工具（如机器人模型、运动控制器）无缝集成，支持从路径规划到运动控制的全流程开发。

5.2 适用范围

• 机器人类型：适用于轮式移动机器人（如无人车、AGV）、差分驱动机器人，尤其适合有最小转弯半径约束的车型；
• 应用场景：室内外结构化环境（如停车场、车间、仓库），需避开静态障碍物，同时要求轨迹平滑、可执行；
• 性能要求：中等计算复杂度，迭代次数（如4次外层迭代、15次内层求解）可满足实时性需求（如10Hz以内的规划频率）。

六、总结

MATLAB中的TEB路径优化算法通过模块化设计，实现了从参考路径生成到轨迹优化的全流程功能，核心优势在于多约束融合与动态节点调整，能够为移动机器人生成安全、平滑、可执行的运动轨迹。通过配置不同的约束参数与目标权重，可适配多种应用场景，是机器人路径规划与运动控制领域的重要工具。

在实际应用中，需根据机器人硬件参数（如最大速度、最小转弯半径）与环境特性（如障碍物密度）调整优化参数，平衡轨迹安全性、平滑性与时间效率，确保优化结果符合实际控制需求。