轮式移动机器人轨迹跟踪的MATHLAB程序,运用运动学和动力学模型的双闭环控制,借鉴自抗扰控制...
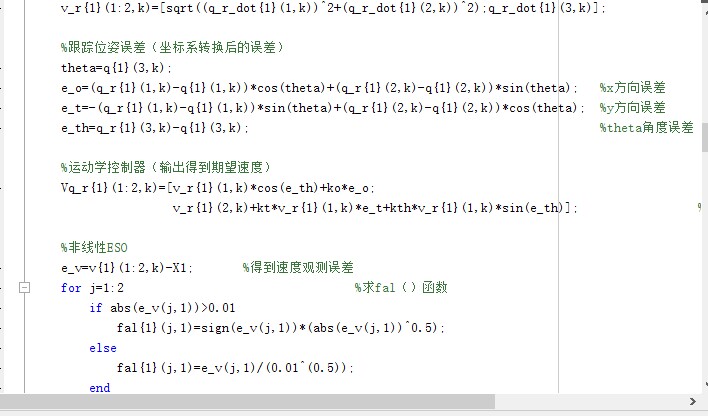
系统当前以圆形轨迹为跟踪目标,其参数由振幅 $A$ 与角频率 $\omega$ 定义。参考位姿 $qr = [xr, yr, \thetar]^\top$ 及其导数可解析生成,进而得到参考线速度与角速度组成的虚拟速度向量 $v_r = [v, \omega]^\top$。为实现稳定跟踪,采用机体坐标系下的位姿误差$e_o$:沿机器人前进方向的位置误差;$e_t$:垂直于前进方向的横向误差;$e_{
轮式移动机器人轨迹跟踪的MATHLAB程序,运用运动学和动力学模型的双闭环控制,借鉴自抗扰控制技术结合了非线性ESO,跟踪效果良好,控制和抗扰效果较优,可分享控制结构图。 这段程序主要是一个小车的动力学仿真程序,用于模拟小车在参考轨迹下的运动。下面我将对程序进行详细的分析解释。 首先,程序开始时使用`clear`、`clc`和`close all`命令来清除工作空间、命令窗口和图形窗口中的内容。 接下来,程序定义了一系列参数和变量,用于设置仿真的参数和存储仿真过程中的数据。这些参数包括小车的质量、车宽、驱动轮半径等,还有参考轨迹的振幅和频率,仿真步长,仿真时间等。 然后,程序定义了一些元胞数组,用于存储不同阶段的数据。这些数组包括参考轨迹位姿、真实运动轨迹位姿、参考轨迹一阶导数、虚拟参考轨迹速度、期望速度、真实速度、控制器输出的控制力矩、控制输入、期望速度与真实速度误差、摩擦值、外界扰动值、总扰动、位姿跟踪误差、扰动观测值等。 接下来,程序给这些变量赋初始值,包括小车的初始位姿和速度,虚拟初始速度,期望初始速度,控制器输出的控制力矩,扰动观测值等。 然后,程序进入一个循环,仿真时间从0到给定的仿真时间tf。在每个循环中,程序根据给定的参考轨迹生成圆形参考轨迹,并计算参考轨迹的一阶导数和虚拟参考轨迹速度。 接下来,程序计算位姿误差,并使用运动学控制器计算期望速度。然后,程序使用非线性ESO(Extended State Observer)估计速度扰动,并使用动力学控制器计算控制力矩。最后,程序根据控制力矩和扰动计算小车的实际速度和位姿,并计算位姿跟踪误差。 在每个循环结束时,程序更新时间和循环索引,并继续下一次循环,直到仿真时间达到设定的结束时间tf。 最后,程序绘制了多个图形来展示仿真结果。这些图形包括参考轨迹和实际运动轨迹的图像、参考轨迹角度和实际角度的图像、内环速度误差的图像、位姿跟踪误差的图像、线速度扰动和观测器估计的图像、角速度扰动和观测器估计的图像、速度曲线的图像和控制量输入的图像。 通过这些图形,可以直观地了解小车在参考轨迹下的运动情况,以及控制器的性能和位姿跟踪误差等。 这段程序涉及到的知识点包括动力学方程、参考轨迹生成、运动学控制器、非线性ESO、动力学控制器等。它主要用于解决小车在给定参考轨迹下的运动控制问题,通过控制器输出的控制力矩来控制小车的速度和位姿,以实现对参考轨迹的跟踪。
本文介绍了一种基于双闭环控制架构的轮式移动机器人轨迹跟踪控制方案,融合了运动学与动力学模型,并引入自抗扰控制(ADRC)中的非线性扩张状态观测器(ESO)技术,显著提升了系统在存在模型不确定性与外部扰动情况下的轨迹跟踪精度与鲁棒性。
1. 系统整体架构
该控制系统采用典型的“外环-内环”双闭环结构:
- 外环(运动学层):负责将参考轨迹(如圆形轨迹)与机器人当前位姿进行比较,通过设计的运动学控制器生成期望的线速度与角速度指令。
- 内环(动力学层):接收外环输出的期望速度,结合实际速度反馈,利用动力学模型与非线性ESO进行扰动估计与补偿,最终生成实际控制输入(如电机电压或力矩)。
这种分层设计有效解耦了路径规划与底层执行,使系统具备良好的模块化与可扩展性。
2. 参考轨迹与误差定义
系统当前以圆形轨迹为跟踪目标,其参数由振幅 $A$ 与角频率 $\omega$ 定义。参考位姿 $qr = [xr, yr, \thetar]^\top$ 及其导数可解析生成,进而得到参考线速度与角速度组成的虚拟速度向量 $v_r = [v, \omega]^\top$。
为实现稳定跟踪,采用机体坐标系下的位姿误差进行反馈设计:
- $e_o$:沿机器人前进方向的位置误差;
- $e_t$:垂直于前进方向的横向误差;
- $e_{th}$:朝向角误差。
该误差定义方式天然具备坐标系一致性,有利于控制器在任意朝向下保持性能。
3. 外环运动学控制器
外环控制器基于误差反馈,将参考速度 $vr$ 与位姿误差融合,生成更合理的期望速度指令 $V{qr}$。其设计充分考虑了非完整性约束,并通过调节增益参数(如 $ko, kt, k{th}$)实现误差的快速收敛。该控制器结构简洁,计算高效,适用于实时嵌入式平台。
4. 内环动力学控制与扰动补偿
内环基于机器人的简化动力学模型,形式为:
$$
M{ba} \dot{V} + F{ba} + \tau{d,ba} = \tau{ba}
$$
其中 $M{ba}$ 为等效质量矩阵,$F{ba}$ 为摩擦力投影,$\tau{d,ba}$ 为未知外部扰动,$\tau{ba}$ 为控制力矩。
关键创新在于引入非线性扩张状态观测器(ESO):
- ESO将系统总扰动(包括摩擦、外部干扰及未建模动态)视为“扩张状态”进行实时估计;
- 采用非线性函数
fal()构建观测器反馈律,兼顾大误差下的快速响应与小误差下的线性特性; - 观测器输出 $X_3$ 即为对总扰动的估计值,用于前馈补偿。
动力学控制器结合速度跟踪误差与扰动估计,生成补偿后的控制力矩 $\tau_{ba}$,再通过逆动力学映射得到实际控制输入 $U$。该策略显著削弱了扰动对系统性能的影响。
5. 仿真验证与性能表现
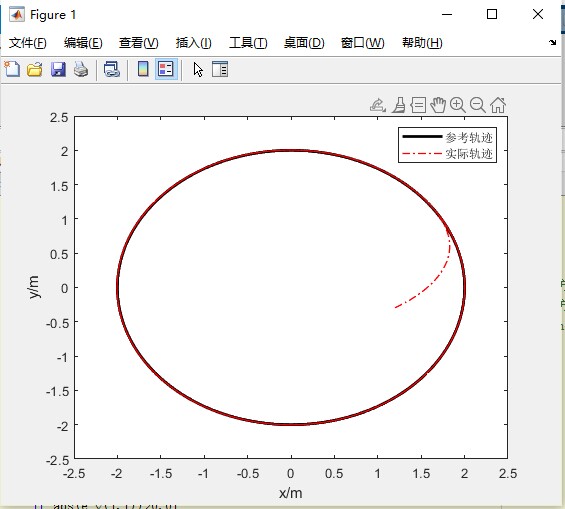
系统在 MATLAB 环境下进行了 50 秒的闭环仿真,结果表明:
- 轨迹跟踪精度高:实际轨迹紧密跟随圆形参考轨迹,位姿误差($ex, ey, e_\theta$)在短时间内收敛至较小范围;
- 扰动估计准确:ESO 对线速度与角速度通道的总扰动均能快速、准确地估计,验证了其观测能力;
- 控制输入合理:尽管存在扰动,控制量保持在合理幅值范围内,未出现剧烈抖振;
- 速度响应良好:期望速度、虚拟速度与实际速度曲线吻合度高,体现内环动态响应迅速。
6. 总结
本方案通过融合运动学规划、动力学建模与自抗扰思想,构建了一个鲁棒性强、跟踪精度高的轮式移动机器人轨迹跟踪系统。其核心优势在于:
- 利用 ESO 实现“扰动观测-补偿”机制,降低对精确模型的依赖;
- 双闭环结构清晰,便于参数整定与工程实现;
- 适用于存在摩擦、负载变化或外部干扰的复杂应用场景。
该框架具有良好的通用性,可进一步扩展至直线轨迹、任意路径跟踪,或迁移至实物机器人平台进行实验验证。

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容





所有评论(0)