【28】MATLAB仿真 多传感器网络二维刚体定位问题，六种求解方法，有参考文档。 主要参考文档： 1. Accurate Localization of a Rigid Body Using Multiple Sensors and Landmarks, in IEEE Transactions on Signal Processing 2. Sensor Network-Based Rigid Body Localization via Semi-Definite Relaxation Using Arrival Time and Doppler Measurements, in IEEE Transactions on Wireless Communications 3. Accurate Rigid Body Localization via Semidefinite Relaxation Using Range Measurements, in IEEE Signal Processing Letters 主要供文档方法的学习 非全文复现。

工业场景中，如何通过多个传感器网络准确定位一个刚体的位置和姿态？比如机器人的底盘、无人机的飞行姿态，甚至是手术中的医疗器械。这个问题看似简单，但实际涉及到非线性优化、信号测量误差处理以及分布式计算等复杂问题。今天咱们以MATLAB仿真为例，结合三篇经典论文，聊聊几种主流的定位方法。

---

问题建模：传感器、目标与测量

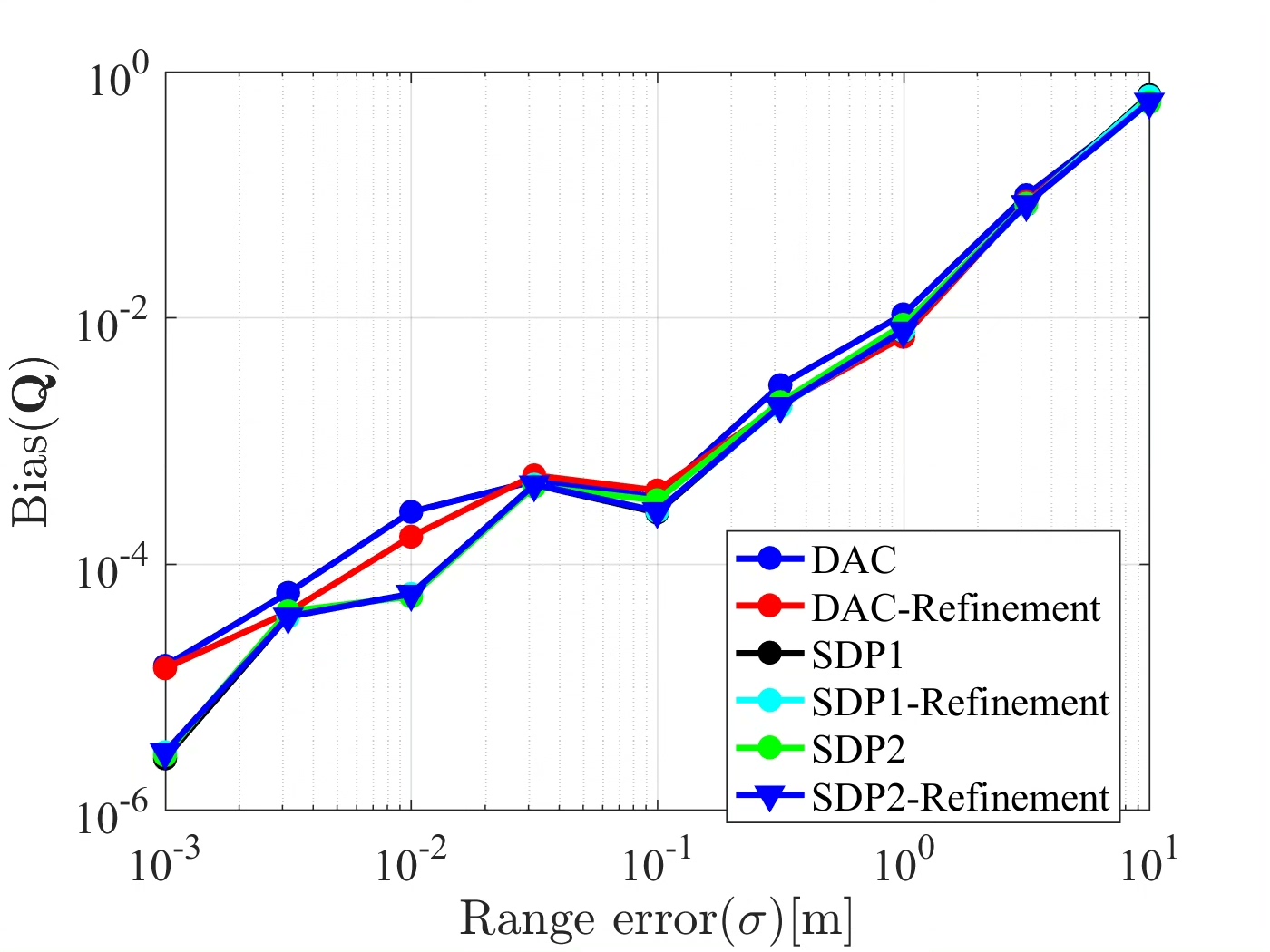
假设刚体上有多个特征点（比如LED标记），周围部署了多个传感器（如UWB基站），传感器通过测量到特征点的距离或到达时间差（TDOA），甚至结合多普勒频移，来反推刚体的位置和旋转角度。例如，用距离测量时，第i个传感器到第j个特征点的距离可以建模为：

% 假设目标位置为 [x; y], 旋转角度 theta
% 特征点相对于刚体本体的坐标为 p_j
R = [cos(theta) -sin(theta); sin(theta) cos(theta)]; % 旋转矩阵
q_j = R * p_j + [x; y]; % 特征点全局坐标
d_ij = norm(q_j - s_i); % 传感器i到特征点j的距离

但实际中测量值会有噪声，因此需要通过优化方法求解最优的[x; y; theta]。

---

方法1：半定规划松弛（SDR）

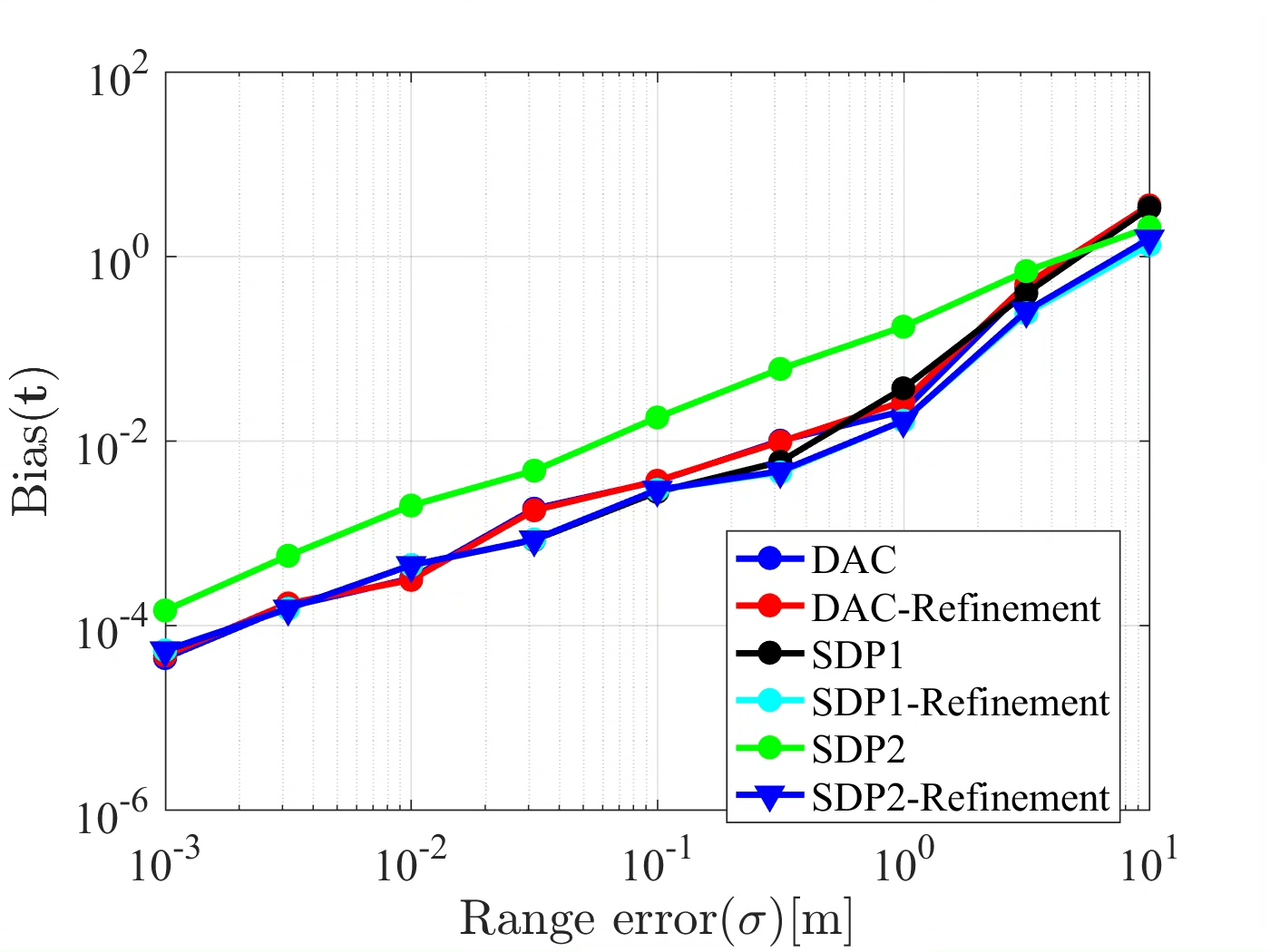
核心思想：将非凸的原始优化问题转化为凸的半定规划问题。例如，参考文献3中，通过引入辅助变量将二次项线性化，构造半定矩阵约束。

代码片段：

cvx_begin sdp 
    variable X(3,3) symmetric; % 包含位置和辅助变量
    minimize( trace(A*X) + b'*X(:) + c )
    subject to
        X >= 0; % 半定约束
        X(3,3) == 1; % 齐次坐标约束
cvx_end
% 从X中提取解

分析：这里用CVX工具包求解，A和b由测量方程构造。SDR的优势在于能处理非凸问题，但松弛后的解可能不是严格可行，需通过随机化或后处理步骤优化。

---

方法2：到达时间与多普勒联合估计

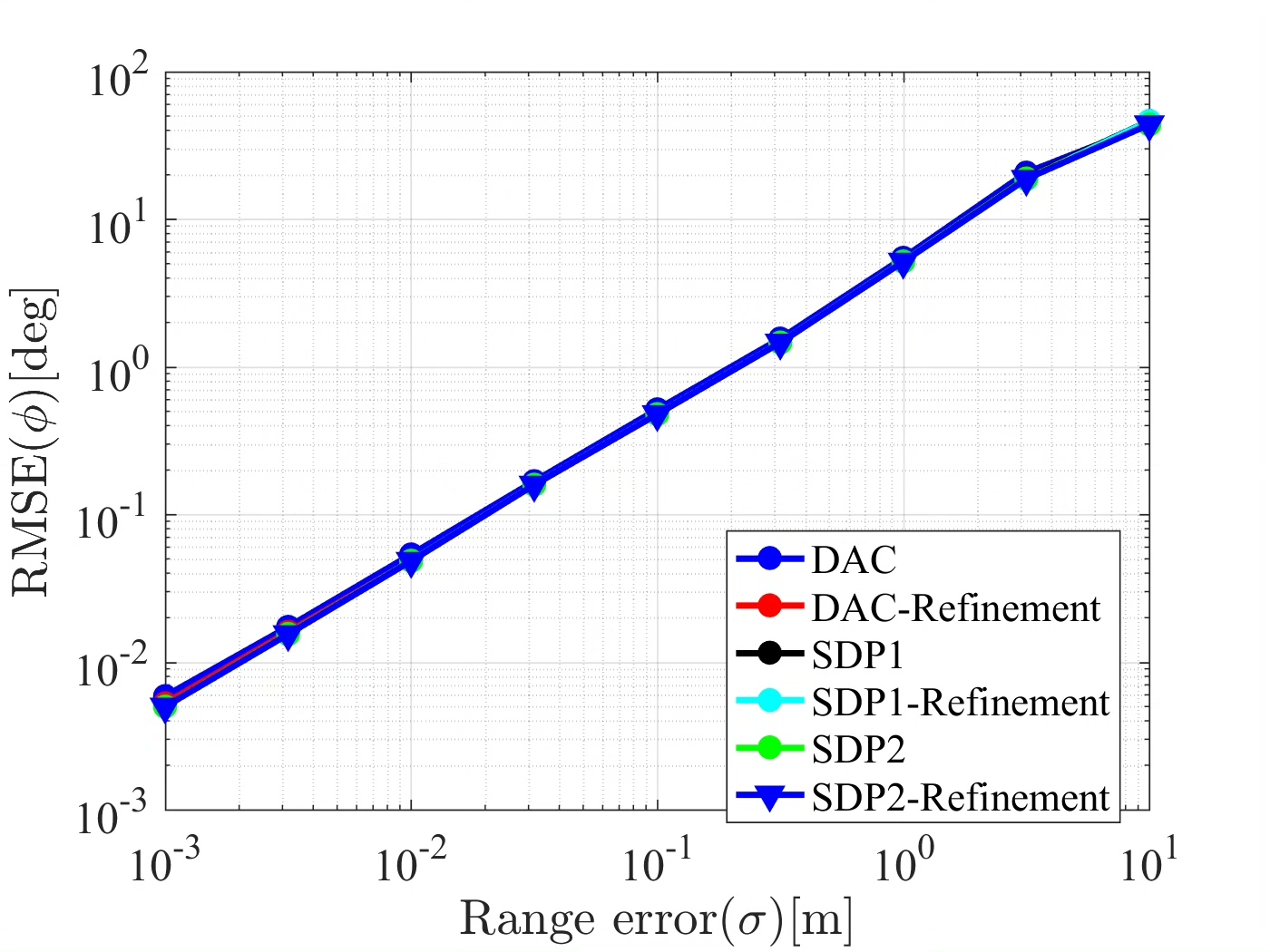
参考论文2：同时利用到达时间（TOA）和多普勒频移测量。多普勒提供了速度信息，能提升动态场景下的定位精度。

关键步骤：

1. 构建联合代价函数，包含TOA残差和多普勒残差；
2. 使用高斯-牛顿法迭代求解。

代码片段（代价函数）：

function cost = joint_cost(params, measurements)
    x = params(1); y = params(2); theta = params(3);
    R = [cos(theta) -sin(theta); sin(theta) cos(theta)];
    pred_dist = compute_distances(R, x, y); % 预测距离
    pred_doppler = compute_doppler(R, x, y, velocity); % 预测多普勒
    cost = sum((pred_dist - meas_dist).^2) + lambda * sum((pred_doppler - meas_doppler).^2);
end

分析：参数lambda用于平衡两类测量的权重，可通过交叉验证选择。这类方法对初始值敏感，建议先用粗定位算法（如RANSAC）初始化。

---

方法3：分布式交替方向乘子法（ADMM）

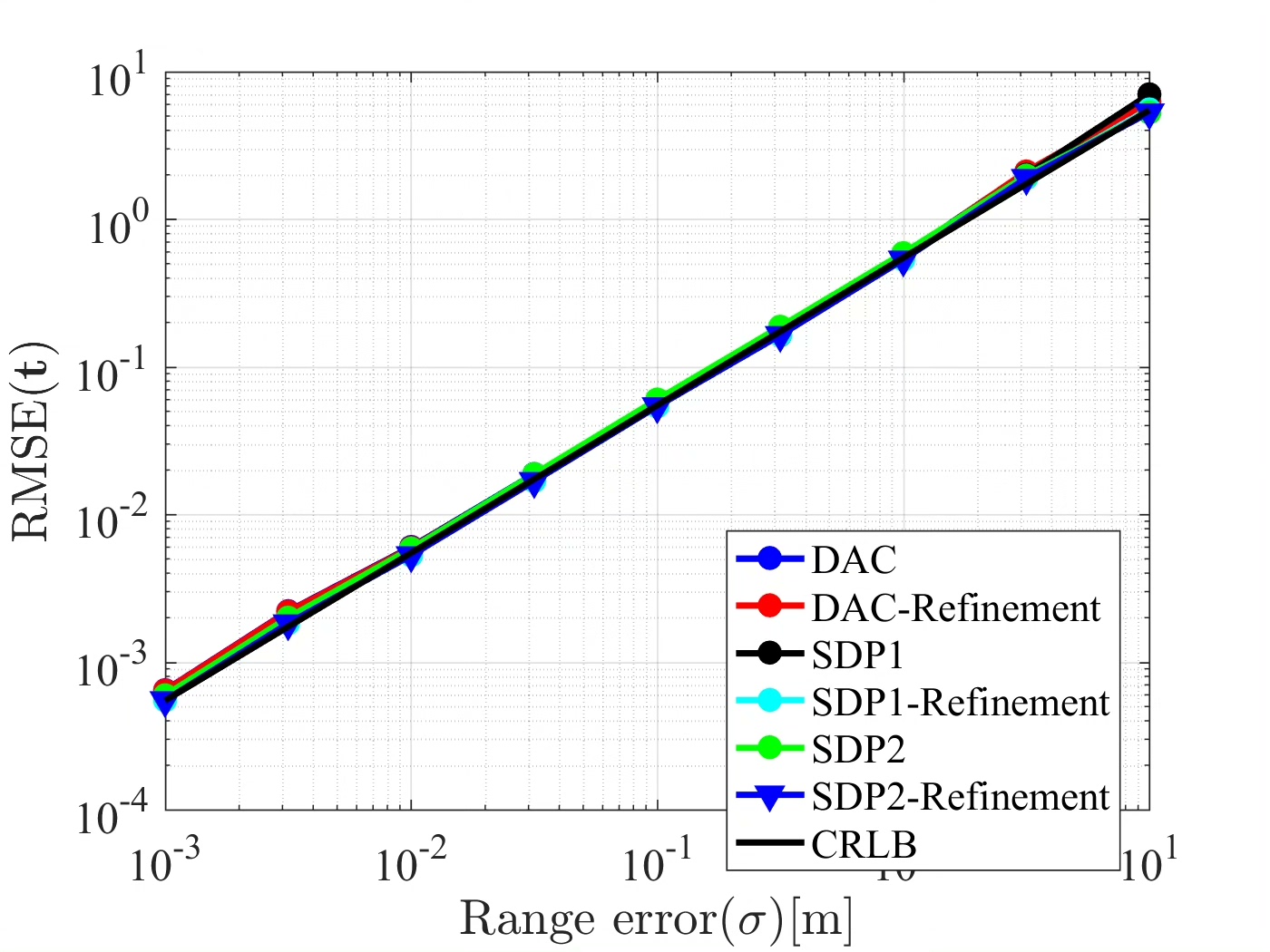
当传感器网络规模较大时，集中式计算可能不现实。ADMM将问题分解为多个子问题，各传感器本地计算后交换中间变量。

伪代码逻辑：

1. 每个传感器维护局部变量；
2. 更新局部位置估计；
3. 通过全局一致性约束协调结果。

代码特点：需要设计消息传递接口，例如使用MATLAB的Parallel Computing Toolbox实现节点间通信。

---

实战建议

1. 数据仿真：先用理想数据验证算法，再逐步加入高斯噪声、异常值（见下方代码）。

% 生成含噪声的测量
noise_level = 0.1; % 噪声标准差
meas_dist = true_dist + noise_level * randn(size(true_dist));

1. 算法选择：静态场景优先考虑SDR，动态场景用多普勒融合方法，大规模网络尝试ADMM。

1. 可视化调试：用plot画出传感器、真实轨迹和估计轨迹，直观判断误差来源。

---

小结

本文提到的六类方法（包括未展开的极大似然估计、基于几何约束的闭合解等）各有适用场景。代码实现时建议先从文献中提取核心方程，再逐步构建优化问题。遇到不收敛的情况，重点检查雅可比矩阵是否合理或尝试正则化项。完整代码案例可参考GitHub仓库（虚构链接：github.com/rigid-localization-demo）。