Hume——系统1(VLM+评估头+动作头)与系统2(动作头)的组合：系统1做慢思考且通过价值评估选择对应的动作片段，让系统2持续扩散去噪

v_JULY_v

1110人浏览 · 2025-12-29 19:03:03

v_JULY_v · 2025-12-29 19:03:03 发布

前言

之所以解读本文介绍的Hume，源于两点

在未来半年内，轮式 + 机械臂 + 夹爪依然是进工厂打工干活的首选，其次轮式人形 + 灵巧手
近期，会有客户给我们寄来一台智元轮式人形，以帮他们做场景化交付

第一部分

1.1 引言与相关工作

1.1.1 引言

如原论文所述，受到人类认知双系统理论的启发，研究者将“思考与推理步骤”引入到大型语言模型（LLMs）中，以增强其在数字领域中解决复杂问题的能力，并取得了显著效果

直观地看，物理世界中的通用机器人同样需要类似的 System-2 慢思考能力，才能执行动态、灵巧且复杂的任务 [14,15,16,17]；
而基于直觉的快速 System-1 思维无法很好地应对精细、脆弱且易出错的机器人动作预测 [18,19,20,21]
因此，对于旨在在多样化场景下解决复杂机器人任务的通用机器人策略而言，一个关键问题是：如何在通用机器人策略中实现有效的 System-2 慢思考，以获得准确的动作预测？

然而，要为通用机器人策略配备 System-2 思维能力，主要面临两个挑战

首先，思考和推理技术主要是在文本模态中得到验证，而细致而脆弱的机器人动作缺乏清晰且一致的语义，这使得很难像在 LLM 中那样进行语义化的 Chain-of-Thought（CoT）[22] 推理
其次，通用机器人策略需要在实时条件下执行灵巧而复杂的任务，因此如何在System-2 思维的“缓慢”与机器人控制所要求的“快速”之间实现有效平衡至关重要

最近，embodied chain-of-thought reasoning（ECoT）[23] 使 VLA 模型能够在选择机器人动作之前预测有用的中间推理文本，从而提升 VLA 模型的泛化能力和性能
然而，执行这些中间推理步骤会显著降低策略推理速度
此外，多项工作[24,25,26,27,28,29] 已将双系统架构引入 Vision-Language-Action 模型中。典型工作Helix [30] 采用预训练的 VLM 主干作为 System 2，同时使用一个更小的网络作为System 1，以输出用于实时控制的高频动作
————
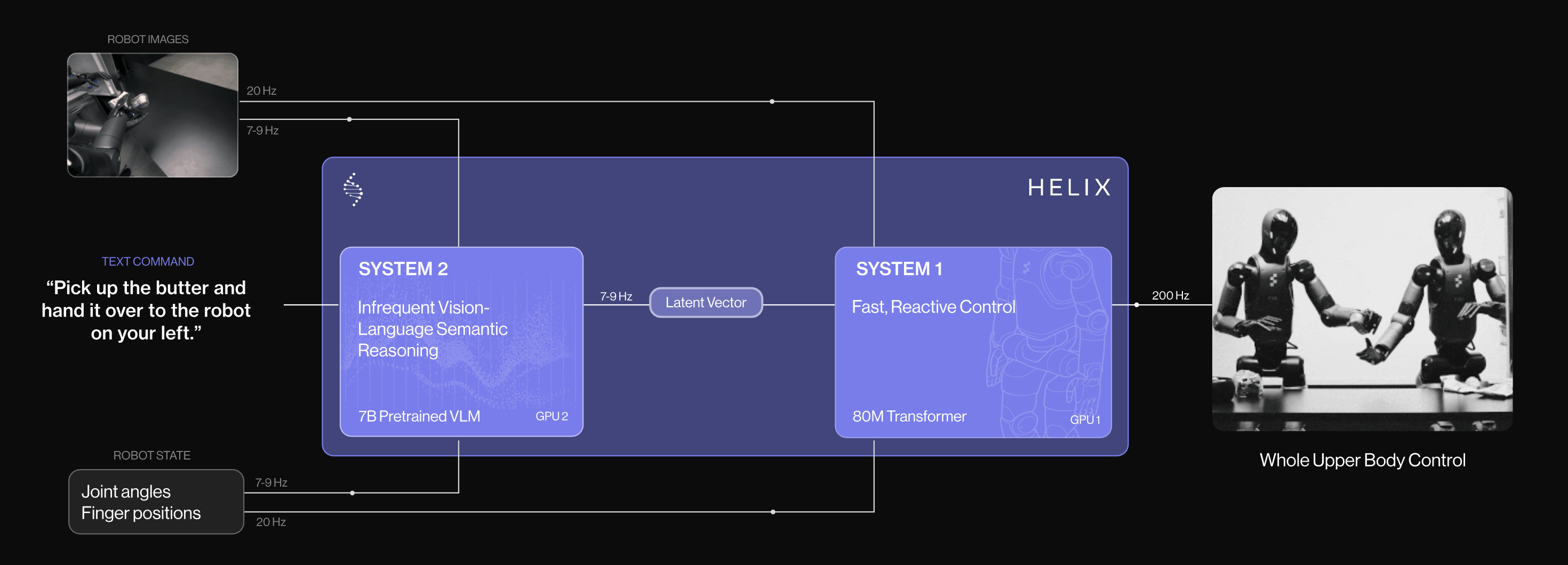
这些方法通常使用潜在向量或细粒度语言指令作为两套系统之间沟通的桥梁。尽管它们具备更快的推理速度，但这些模型中的System 2 并未进行有效的思考与推理来指导 System-1 的动作预测

在这项工作中，来自1 Shanghai Jiao Tong University、2 Shanghai AI Laboratory、3 Fudan University、4 AgiBot、5 INSAIT, Sofia University、6 Zhejiang University、7Northwestern Polytechnical University的研究者提出了一种双系统视觉-语言-行动模型 Hume

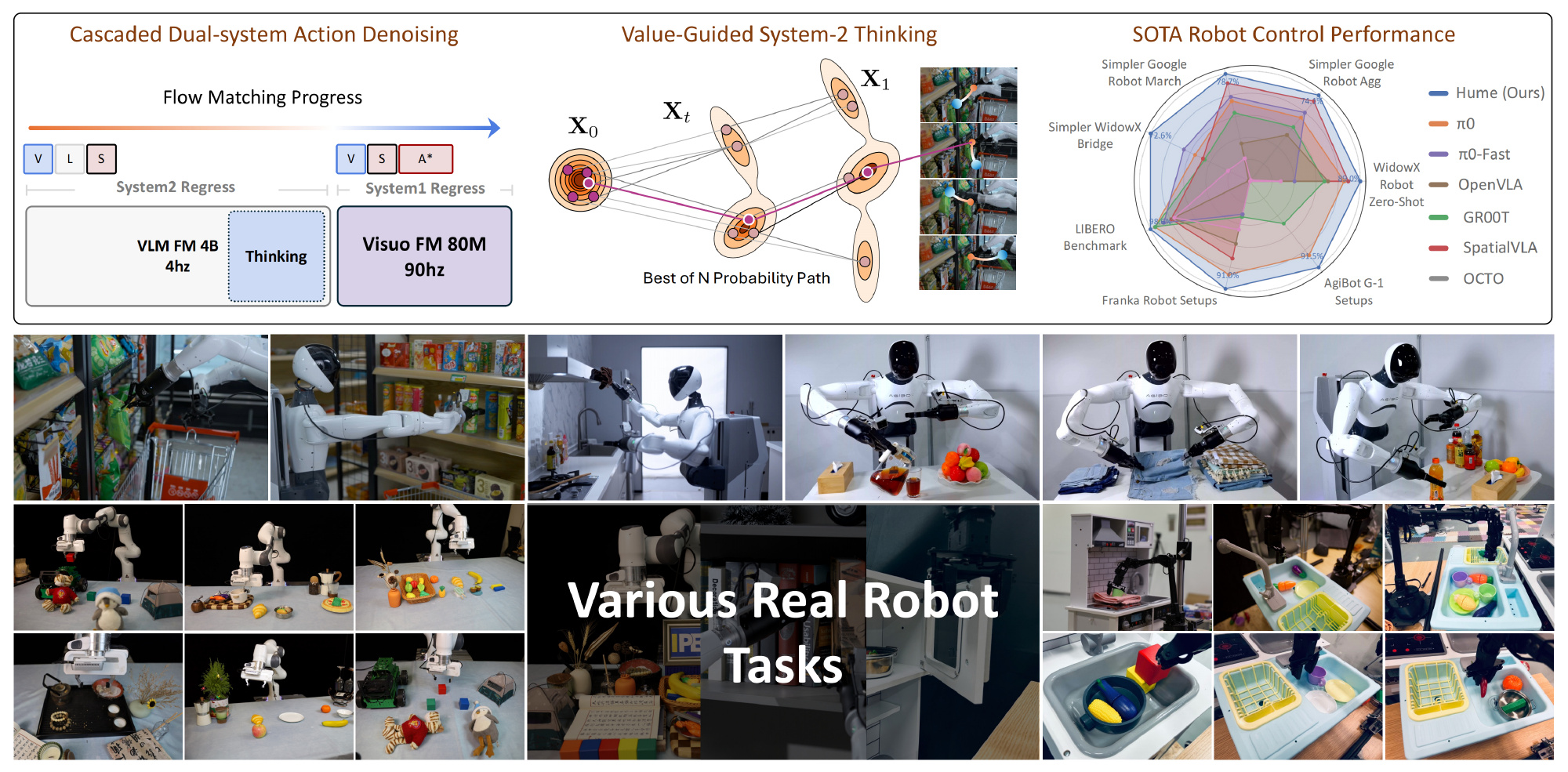
其论文地址为：Hume: Introducing System-2 Thinking in Visual-Language-Action Model
其作者包括
Haoming Song1,2∗、Delin Qu3,2∗、Yuanqi Yao5,2、Qizhi Chen6,2、Qi Lv2 Yiwen Tang2
Modi Shi4、Guanghui Ren4、Maoqing Yao4、Bin Zhao2,7、Dong Wang2†、Xuelong Li2,7†
其项目地址为：hume-vla.github.io
其GitHub地址为：github.com/hume-vla/hume

具体而言，该模型通过价值引导的重复采样和级联动作去噪，为 VLA 模型注入具备 System-2（系统 2）思维能力的机制

Hume 的 System 2 构建在一个预训练的视觉-语言模型VLM之上，并在其上附加了两个专用头：

$\rightarrow$ 一个基于 flow matching [31,32] 的去噪头，用于预测机器人动作
$\rightarrow$ 一个价值查询头value-query head，用于估计预测动作的状态-动作价值
它处理机器人的观测V 和语言指令L，并通过动作去噪头预测长时间跨度的动作片段

随后，在给定预测动作片段的条件下，估计相应的状态-动作价值
价值引导的思考通过对多个动作片段进行重复采样，并选择价值最高的那一个来实现
对于 Hume 的 System 1(系统 1)，它从 System 2 所选的长时间跨度动作片段中取出一个短片段，再结合当前视觉观测和机器人状态，随后通过级联动作去噪，利用一个独立的轻量级扩散策略生成最终流畅的机器人动作
在部署阶段，System 2 以较低频率(4 Hz)执行价值引导的思考，而 System 1 异步接收 System 2选出的动作片段，并以实时频率(90 Hz)预测流畅动作

总之，借助所提出的价值引导思考与级联动作去噪机制，Hume 探索了强大的 System 2 慢思考范式，以增强 VLA 模型

1.1.2 相关工作

首先，对于双系统视觉-语言-动作模型

近期，多项研究 [1,2,4,35,36,37,38,39,40,41,6,26,30,24] 将VLM 扩展用于机器人控制
RT-2 [2] 使用离散化的动作 token 对 PaLI-X [42] 进行微调，而 OpenVLA [4] 则在 OXE 数据集 [44] 上适配 Prismatic VLM [43]
π0[12] 将PaliGemma 与 flow-matching 相结合，以处理连续动作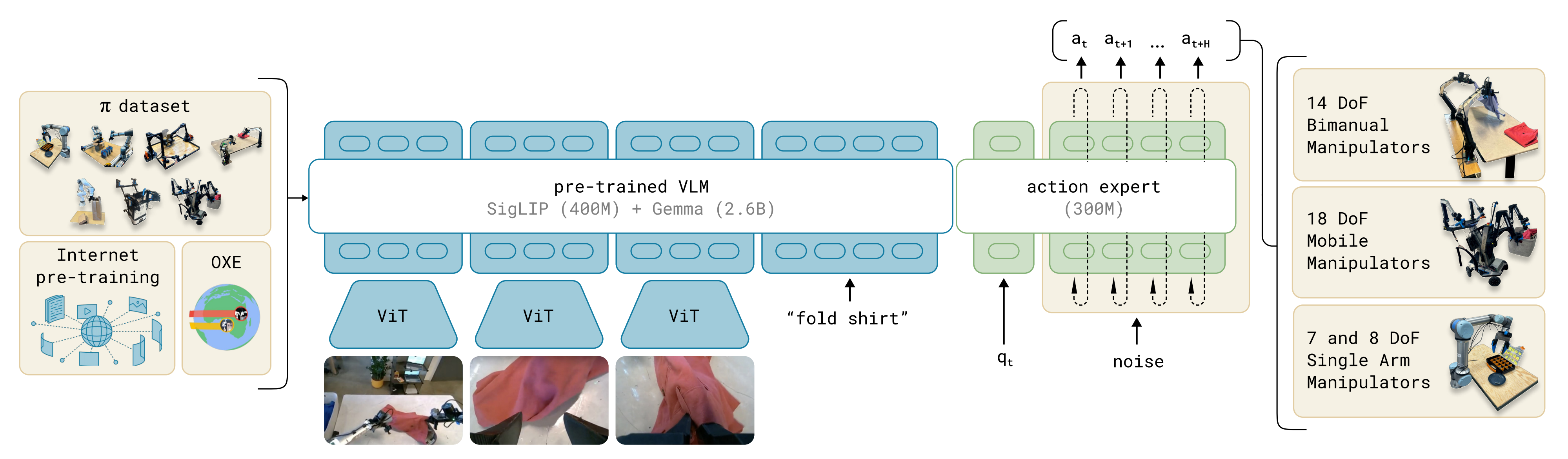
为解决效率与集成方面的挑战，出现了双系统架构
HiRT [25] 以低频运行 VLM，同时保持基于视觉的高频控制，以实现实时交互
DexVLA [27] 使用扩散式动作专家，并结合具身课程学习（embodimentcurriculum learning），跨多种机器人类型进行训练
GR00T N1 [28] 提出了一个专为人形机器人设计的端到端训练双系统
Gemini Robotics [11] 构建在 Gemini 2.0 之上，配备专门用于控制和推理的模型
HiRobot [29] 支持在情境化反馈下处理复杂指令
————
与单体式架构相比，这些方法在效率、成功率和适应性方面均有所提升

其次，对于System 2 与 System-2 思维

大量研究 [22,45,46,47,48,49,50,51,52] 探索了 System 2推理方法，以增强 LLM 的问题求解能力
Chain-of-Thought [22,53] 在给出答案之前引入中间推理步骤，而 Tree-of-Thoughts [52] 通过自我验证探索多条解题路径
Reflexion[45] 使模型能够对先前的尝试进行语言化反思
System-2 Thinking 框架显式建模类人式的深思熟虑过程
SETS [54] 将自我批判、多条推理路径与多数投票相结合
SC-MCTS [55] 融合多个奖励模型，以实现更稳健的树搜索
为应对效率方面的担忧，O1-Pruner [56] 通过引入长度惩罚损失来构建精炼的推理过程
————
尽管这些方法已经提升了在语言任务中的推理能力，但它们在视觉-语言-动作模型中的应用仍然基本未被探索

最后，对于级联去噪

级联去噪（Cascaded Denoising）[57] 最初作为一种扩散模型（diffusion model）[58] 被提出，其通过级联系统生成更高分辨率的图像。它从一个低分辨率扩散模型开始，对生成的图像不断进行上采样，以获得高分辨率结果
f-DM [59] 通过函数学习在各级之间施加变换，实现逐级的信号恢复
Cas-DM [60] 级联噪声预测和图像预测模块，将感知损失集成到扩散模型中
SCDM[61] 在光谱维度上进行级联生成，逐步重建高光谱波段

HiFI [62] 通过级联一致分辨率的小块，实现内存高效的高分辨率帧插值
CDM-VTON [63] 采用两阶段级联，用于虚拟试衣（virtual try-on）应用
————
尽管这些方法在图像领域显著提升了能力，但将级联去噪用于整合 System 1 与 System 2 的研究仍然基本未被探索

1.2 Hume的完整方法论

本节将详细介绍 Hume 模型的架构及其训练与部署策略

第 1.2.1 节详细描述了在状态-动作价值估计器帮助下实现的 Value-Guided System-2 Thinking 过程
第 1.2.2 节，将阐述 System 1 模块与 System 2 模块如何通过所提出的级联动作去噪机制进行异步协作
第 1.2.3 节解释该模型的多阶段训练和部署策略

1.2.1 System 2：价值引导的系统2思维

如图2 所示

System 2 模块被实例化为基于预训练VLM构建的VLA

形式上，System 2 模块的输入由时间步 $t$ 的RGB 图像 $\mathbf{i}_{t}=\left[\mathbf{I}_{t}^{1}, \ldots, \mathbf{I}_{t}^{n}\right]$ 、自然语言指令 $\ell_{t}$ 和机器人状态信息 $\mathbf{s}_{t}$ 组成
与VLA 模型类似，作者首先为VLM 主干网络添加一个动作去噪头，以学习一个映射函数 $\mathcal{F}(\cdot)$ ，从观测 $\mathbf{o}_{t}$ 生成候选机器人动作 $\mathbf{A}_{t}$ ，即 $\mathbf{A}_{t}=\mathcal{F}\left(\mathbf{o}_{t}\right)$
此外，为了赋予Hume System-2 思维能力，作者在VLM 主干网络上附加另一个价值查询头value-query head，用于估计候选机器人动作 $\mathbf{A}_{t}$ 的状态-动作价值 $Q_{\theta}\left(\mathbf{q}_{t}, \mathbf{A}_{t}\right)$

首先，对于候选动作生成

候选机器人动作由一个动作去噪头(action denoising head)生成，其目标是建模数据分布 $p\left(\mathbf{A}_{t} \mid \mathbf{o}_{t}\right)$ ，其中 $\mathbf{o}_{t}$ 由图像 $\mathbf{i}_{t}$ 、语言指令 $\ell_{t}$ 和机器人状态信息 $\mathbf{s}_{t}$ 组成
它被实现为一种基于transformer的流匹配去噪过程，用于预测” 含噪动作” $\mathbf{A}_{t}^{\tau}$ 中的剩余动作噪声 $\mathbf{v}_{\theta}\left(\mathbf{A}_{t}^{\tau}, \mathbf{o}_{t}\right)$ ，其中 $\tau \in[0,1]$ 是表示动作噪声水平的流匹配时间步
从随机噪声 $\mathbf{A}_{t}^{0} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$ 出发，去噪头通过使用前向Euler 方法，逐步去除 $\mathbf{A}_{t}^{0}$ 中的噪声直到 $\mathbf{A}_{t}^{1}$ 来生成动作： $\mathbf{A}_{t}^{\tau+\delta}=\mathbf{A}_{t}^{\tau}+\delta \mathbf{v}_{\theta}\left(\mathbf{A}_{t}^{\tau}, \mathbf{o}_{t}\right)$ ，其中 $\delta$ 是去噪步长

在实践中，作者使用10 个去噪步，对应于 $\delta=0.1$

在训练过程中，对于从数据集中采样的真实动作 $\mathbf{A}_{t}$ ，在给定观测 $\mathbf{o}_{t}$ 和含噪动作 $\mathbf{A}_{t}^{\tau}=\tau \mathbf{A}_{t}+(1-\tau) \epsilon$ 作为输入的情况下，通过最小化实际剩余噪声 $\epsilon-\mathbf{A}_{t}$ 与网络输出 $\mathbf{v}_{\theta}\left(\mathbf{A}_{t}^{\tau}, \mathbf{o}_{t}\right)$ 之间的损失来优化去噪头
训练完成后，在时间步 $t$ 上给定相同的观测 $\mathbf{o}_{t}$ ，动作去噪头通过分别将学习到的向量场 $\mathbf{v}_{\theta}\left(\mathbf{A}_{t}^{\tau}, \mathbf{o}_{t}\right)$ ——从 $\tau=0$ 积分到 $\tau=1-(n-1) \xi$ ，在不同噪声水平下生成 $N$ 个候选机器人动作块 $\mathbf{A}_{t}^{\tau_{n}} \in\left\{\mathbf{A}_{t}^{\tau_{1}}, \mathbf{A}_{t}^{\tau_{2}}, \ldots, \mathbf{A}_{t}^{\tau_{N}}\right\}$

$\mathbf{A}_{t}^{\tau_{n}}=\int_{0}^{1-(n-1) \xi} \mathbf{v}_{\theta}\left(\mathbf{A}_{t}^{\tau}, \mathbf{o}_{t}\right) d \tau+\mathbf{A}_{t}^{0}$
其中 $\xi$ 用于控制相邻候选之间的噪声间隔, 且 $\mathbf{A}_{t}^{0}$ 是从正态分布 $\mathbf{A}_{t}^{0} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$ 中采样得到的初始动作，注意 $n \in\{1,2, \ldots, N\}$ , 这导致大多数生成的候选动作 $\mathbf{A}_{t}^{\tau_{n}}$ 未被完全去噪

其次，对于状态-动作价值估计

状态-动作价值通过在相同的VLM 骨干上构建所提出的value-query head并学习一个潜在条件Q 函数来进行估计

value-query head 由两个用于估计状态-动作价值的评论家网络以及一个用于辅助评论家网络训练的行为者网络组成
————
具体地，一个特殊的查询token $\mathbf{q}_{t}$ 被引入并附加在VLM 输入序列的末尾，它是一个可学习的token，具有与语言token 相同的嵌入维度
然后，对于一个动作块 $\mathbf{A}_{t}$ （可以是真实动作 $\mathbf{A}_{t}^{\mathrm{GT}}$ 或候选动作 $\mathbf{A}_{t}^{\tau_{n}}$ ），将其与这个特殊的查询token $\mathbf{q}_{t}$ 组合后输入到value-query head 中
由于其位于输入序列的最后位置，查询token $\mathbf{q}_{t}$ 可以关注所有先前的token，并且从VLM 输入中聚合必要的信息，在时间步 $t$ 的当前RGB 图像 $\mathbf{i}_{t}=\left[\mathbf{I}_{t}^{1}, \ldots, \mathbf{I}_{t}^{n}\right]$ ，自然语言指令 $\ell_{\mathbf{t}}$
————
通过这种方式, 价值-查询头估计动作块 $\mathbf{A}_{t}^{\tau_{n}}$ 在输入查询token $\mathbf{q}_{t}$ 条件下的状态-动作价值 $Q_{\theta}\left(\mathbf{q}_{t}, \mathbf{A}_{t}^{\tau_{n}}\right)$
该价值-查询头在具有真实动作 $\mathbf{A}_{t}$ 的预先收集的机器人示教数据集上通过离线RL [64] 进行训练
作者使用遵循[65] 的奖励函数构建训练数据集 $\mathcal{D}$ ，其中一个机器人回合中最后3 个转移的奖励被定义为+1, 其余为0
在训练过程中, 作者使用校准的Q-learning 算法[66] 来优化价值-查询头
为了验证该套训练流水线可以有效地优化value-query head，作者将真实动作 $\mathbf{A}_{t}^{\mathrm{GT}}$ 和候选动作 $\mathbf{A}_{t}^{\tau_{n}}$ 以及它们对应的状态-动作价值 $Q\left(\mathbf{q}_{\mathbf{t}}, \mathbf{A}_{t}^{\tau_{n}}\right)$ 投影到同一空间,generating the value map in Fig. 3
该价值图由代表不同状态-动作价值大小的区域组成，而真实动作全部位于高价值区域，这证明value-query head 可以估计合理的状态-动作价值。详细分析可以在附录. A. 2 中找到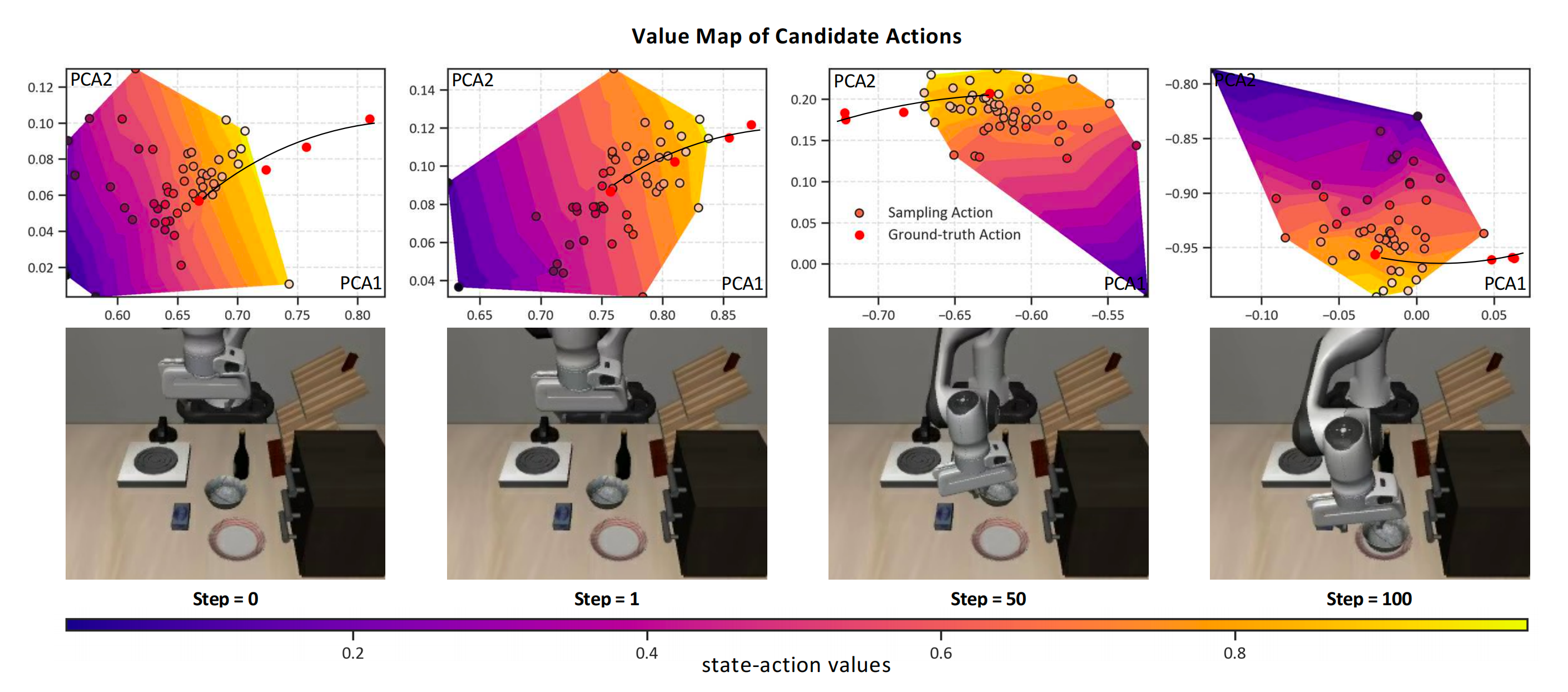

最后，对于价值引导式思考

System-2 的价值引导式思考是通过Best-of-N 选择策略实现的，被选中的动作片段被传递给System 1 以进行级联动作去噪
————
Specifically, 在相同观测条件下，动作去噪头会在不同的噪声水平下生成N 个候选动作片段 $\left\{\mathbf{A}_{t}^{\tau_{1}}, \mathbf{A}_{t}^{\tau_{2}}, \ldots, \mathbf{A}_{t}^{\tau_{N}}\right\}$
然后，这些候选被传递到价值查询头以估计其状态-动作价值。在估计的状态-动作价值的引导下，选择价值最高的动作作为传递给System 1 的最优候选 $\mathbf{A}_{t}^{\tau^{*}}$ ，表示为 $\mathbf{A}_{t}^{\tau^{*}}=\arg \max _{\mathbf{A}_{t}^{\tau_{n}}} Q\left(\mathbf{q}_{\mathbf{t}}, \mathbf{A}_{t}^{\tau_{n}}\right)$ ，其中 $n=1 \ldots N$
在附录A.1 中，作者在模拟的Push-T 任务中进一步可视化了这一过程

1.2.2 System 2和1下：级联双系统动作去噪

为了实现快速、灵敏的机器人控制，System 1 模块需要在推理上轻量且高速。具体而言，System 1 由一个DINOv2-small 视觉编码器和一个用于级联动作去噪的轻量级transformer组成

给定来自System 2 选出的候选动作片段 $\mathbf{A}_{t}^{\tau^{*}}$ ，System 1 模块将观测 $\tilde{\mathbf{o}}_{t+k h}$ 『包括当前图像 $\mathbf{i}_{t}=\left\{\mathbf{I}_{t}^{1}, . ., \mathbf{I}_{t}^{n}\right\}$ 、机器人状态 $\mathbf{s}_{t}$ 』，以及从所选候选 $\mathbf{A}_{t}^{\tau^{*}}$ 中分割出的子动作片段 $\tilde{\mathbf{A}}_{t}$ 作为输入，并通过在子动作片段 $\tilde{\mathbf{A}}_{t}$ 上持续去噪来生成精细化的机器人动作
具体而言, 在时间步 $t$ , 从System 2 中选取的动作片段为 $\mathbf{A}_{t}^{\tau^{*}}=\left[\mathbf{a}_{t}, \mathbf{a}_{t+1}, \ldots, \mathbf{a}_{t+H-1}\right]$ , 然后 $\mathbf{A}_{t}^{\tau^{*}}$ 被划分为 $K:=H / h$ 个子动作片段 $\left\{\tilde{\mathbf{A}}_{t}, \tilde{\mathbf{A}}_{t+h}, \ldots, \tilde{\mathbf{A}}_{t+(K-1) h}\right\}$ , 每个子动作片段的时间跨度为 $h$
————————————
System 1在观测 $\tilde{\mathbf{o}}_{t+k h}$ 的条件下按顺序对这些子动作片段执行级联去噪。注意System 1 比System 2 快得多, 因此System 1 可以在下一段动作片段 $\mathbf{A}_{t}^{\tau^{*}}$ 到来之前完成对所有子动作片段的级联去噪

System 1模块使用System 2 的动作去噪头，并采用相同的流匹配(flow matching)损失进行训练(定义为公式2)：
$L^{\omega}(\theta)=\mathbb{E}_{p\left(\tilde{\mathbf{A}}_{t+k h} \mid \tilde{\mathbf{o}}_{t+k h}\right), q\left(\tilde{\mathbf{A}}_{t+k h}^{\omega} \mid \tilde{\mathbf{A}}_{t+k h}\right)}\left\|\mathbf{v}_{\theta}\left(\tilde{\mathbf{A}}_{t+k h}^{\omega}, \tilde{\mathbf{o}}_{t+k h}\right)-\mathbf{u}\left(\tilde{\mathbf{A}}_{t+k h}^{\omega} \mid \tilde{\mathbf{A}}_{t+k h}\right)\right\|^{2}$
其中上标 $\omega$ 表示System 1 中的流匹配时间步

注意，从System 2 生成的候选动作块并未被完全去噪，即 $\tilde{\mathbf{A}}_{t+k h}^{\tau^{*}} \neq \tilde{\mathbf{A}}_{t+k h}^{1}$ ，这就需要进行连续去噪以保证动作预测的准确性

借鉴图像生成中的连续去噪方法[57]，System 1 通过从 $\omega= 0$ 到 $\omega=1$ 对学习到的向量场进行积分来细化动作

与从随机噪声开始不同，System 1的积分过程从子动作块 $\tilde{\mathbf{A}}_{t+k h}^{\tau^{*}}$ 开始：
$\tilde{\mathbf{A}}_{t+k h}^{\omega}=\int_{0}^{\omega} \mathbf{v}_{\theta}\left(\tilde{\mathbf{A}}_{t+k h}^{\omega}, \tilde{\mathbf{o}}_{t+k h}\right) d \omega+\tilde{\mathbf{A}}_{t+k h}^{\tau^{*}}$
其中 $\mathbf{v}_{\theta}\left(\tilde{\mathbf{A}}_{t+k h}^{\omega}, \mathbf{o}_{t+k h}\right)$ 是由System 1 学习得到的向量场

利用前向欧拉方法
$\tilde{\mathbf{A}}_{t+k h}^{\omega+\sigma}=\tilde{\mathbf{A}}_{t+k h}^{\omega}+\delta \mathbf{v}_{\theta}\left(\tilde{\mathbf{A}}_{t+k h}^{\omega}, \tilde{\mathbf{o}}_{t+k h}\right)$ , System 1 通过10 个去噪步骤(对应于 $\delta=0.1$ ) 生成最终去噪后的动作 $\tilde{\mathbf{A}}_{t+k h}^{1}$

在所有K 个子动作块都已被System 1 处理之后, System 2 将生成一个新的选定动作块 $\mathbf{A}_{t+H}^{\tau^{*}}$ , 并且System 1 将继续从新的选定动作块中细化片段

1.3.3 训练与部署策略

Hume 的训练过程包含两个阶段

在第一阶段，首先使用类似于式 (2) 的流匹配损失
$L^{\omega}(\theta)=\mathbb{E}_{p\left(\tilde{\mathbf{A}}_{t+k h} \mid \tilde{\mathbf{o}}_{t+k h}\right), q\left(\tilde{\mathbf{A}}_{t+k h}^{\omega} \mid \tilde{\mathbf{A}}_{t+k h}\right)}\left\|\mathbf{v}_{\theta}\left(\tilde{\mathbf{A}}_{t+k h}^{\omega}, \tilde{\mathbf{o}}_{t+k h}\right)-\mathbf{u}\left(\tilde{\mathbf{A}}_{t+k h}^{\omega} \mid \tilde{\mathbf{A}}_{t+k h}\right)\right\|^{2}$
对 VLM 主干网络以及 System 2 的动作去噪头进行训练，以确保 System 2 能够预测出可靠的动作
在第二阶段的训练中，将 VLM 主干网络和 System 2 的动作去噪头冻结不再更新，而从头开始训练 System 1 以及 System 2 的 Value-Query 头
————
Value-Query 头的训练目标是在带有正则项的情况下最小化 Bellman 误差，其定义如下：
$\min _{\theta} \alpha \mathcal{R}(\theta)+\frac{1}{2} \mathbb{E}_{\mathbf{q}_{t}, \mathbf{A}_{t}, \mathbf{q}_{t}^{\prime} \sim \mathcal{D}}\left[\left(Q_{\theta}\left(\mathbf{q}_{t}, \mathbf{A}_{t}\right)-\mathcal{B}^{\pi} \bar{Q}\left(\mathbf{q}_{t}, \mathbf{A}_{t}\right)\right)^{2}\right]$

其中 $\mathcal{R}(\theta)$ 是一种经过校准的保守正则项，旨在防止对 Q 值的过高估计，
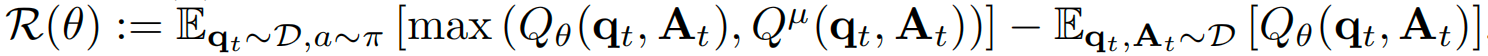
而 $\mathcal{B}^{\pi} \bar{Q}\left(\mathbf{q}_{t}, \mathbf{A}_{t}\right)$ 是应用于延迟目标 Q 网络 $Q_{\bar{\theta}}$ 的备份算子

在推理阶段, System 2 和System 1 模块通过异步机制协同工作以提升整体控制频率

具体而言, 在初始时间步t , System 2 的动作去噪头以4 Hz 的频率生成N = 5 个时域为H = 30的候选动作块 $\mathbf{A}_{t}^{\tau_{n}} \in\left\{\mathbf{A}_{t}^{\tau_{1}}, \mathbf{A}_{t}^{\tau_{2}}, \ldots, \mathbf{A}_{t}^{\tau_{N}}\right\}$ 。随后选出的最优候选动作 $\mathbf{A}_{t}^{\tau^{*}}$ 被存入一个共享队列中
然后, 将 $\tilde{\mathbf{A}}_{t}^{\tau^{*}}$ , 一个时域为h = 15 的子动作块, 从 $\mathbf{A}_{t}^{\tau^{*}}$ 的前h 个时间步中截取出来并传入System 1
System 1 从 $\tilde{\mathbf{A}}_{t}^{\tau^{*}}$ 中去除剩余噪声, 以6 Hz 的频率生成完全去噪的动作 $\tilde{\mathbf{A}}_{t}$ , 并立即在真实机器人上执行全部h = 15 个动作, 从而得到整体90 Hz 的机器人动作控制频率

当机器人执行完 $\tilde{\mathbf{A}}_{t}$ 中全部 $K=H / h=2$ 个子动作块后,System 1 会反复从共享队列中获取最新选出的动作块, 以进行后续的动作去噪
————
由于System 2 和System 1 的工作频率不同, 它们以异步方式协同, 在缓慢的类人思考和快速、具反应性的真实机器人控制之间实现平衡