作者｜岑嘉诚 阿里巴巴达摩院实习生

摘要

 

等变图神经网络（Equivariant Graph Neural Networks, GNNs）在多种应用中已展现出显著成功。为了实现完备性——即在等变函数空间上的通用逼近性质——网络必须能够有效捕捉不同节点之间复杂的多体相互作用。以往的方法通常通过加深网络结构、提高交互阶数或增加可导向特征的维度来实现，但往往伴随着巨大的计算开销，且缺乏多项式时间的解法。在本文中，我们提出了一个具有坚实理论基础的框架，用于构建既高效又实用的完备等变图神经网络。我们证明了：只需两个关键组成部分就能实现完备的等变图神经网络——1)一个完备的标量函数，被称为几何图的标准型；2) 一个满秩的可操控基集合。基于这一发现，我们提出了一种高效算法，能够利用两类常见模型（EGNN 和 TFN）来构建完备的等变图神经网络。实验结果表明，我们的模型在仅使用少量层数的情况下，便能实现更强的完备性与优异的性能，从而显著降低计算开销，同时保持良好的实用效果。

 

论文地址：https://arxiv.org/abs/2510.13169

代码仓库：https://github.com/GLAD-RUC/Uni-EGNN

 

 

近年来，Equivariant Graph Neural Networks（等变图神经网络）已成为分子动力学模拟、晶体结构建模以及力场学习中的主流模型路线。EGNN、PaiNN、TFN、MACE 等模型广泛应用于各类领域，其表现证明了“空间等变性”在物理系统建模中的必要性。

 

现有主流方法可大致归为两类：

 

标量化模型（Scalarization-based），如 EGNN / PaiNN / HEGNN： 利用距离、角度、径向基等标量调节向量信息；

 

张量积模型（Tensor-product-based），如 TFN / MACE / SE(3)-Transformer： 采用 Clebsch–Gordan 展开构造高阶可操作特征实现 SO(3)/O(3) 等变。

 

 

 

由于科学智能任务的复杂性，评判等变模型表达能力的一个重要指标是其是否具备完备性（Completeness），即能对于任意的目标函数具有万能逼近性。在过去，业界普遍认为，尽管基于张量积的模型计算复杂度随多体阶数 (body-order)与球张量阶数（degree）增长快速上升，但其具备更高表达能力——在理想条件下，使用足够高阶球张量特征且堆叠层数足够的张量积模型（如TFN）是完备的。而对于标量化的模型而言，尽管实际实践中，其在效果与效率上往往同时优于张量积模型，但其是否具有完备性依旧是一个有待商榷的问题。

 

本文正是在这一背景下提出：完备的等变图神经网络不应是依赖多层结构或高阶展开去“逼近”目标函数，而是应当在理论上具备“对任意几何结构都可区分 / 可表达”的能力。为此，需要重新审视当前 Equivariant GNN 框架的构造方式。

 

 

 

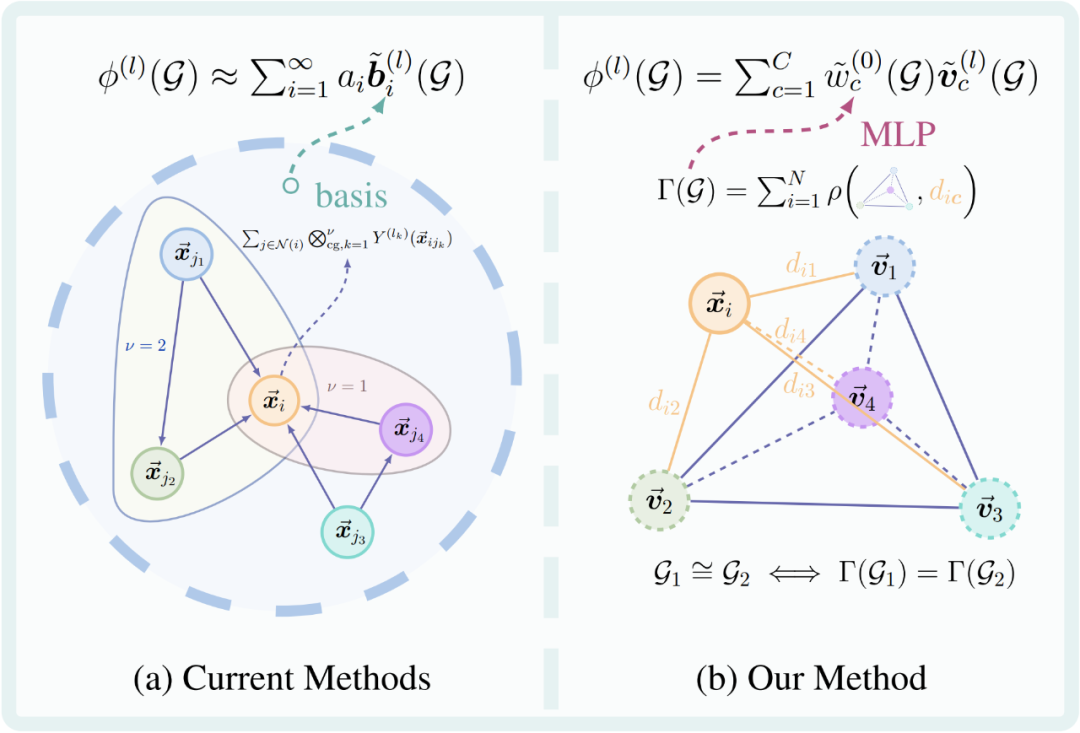
如图(a)所示，传统的张量积模型事实上是采用了一种类似由单变量函数扩展至多变量函数的朴素思想，不断构造函数所需的基。尽管这种方式易于理解，但是计算开销极其昂贵，且只有在极其理想的情况下才能实现完备性。而图(b)则展示了我们的思路，无论神经网络内部发生了什么，其最终的输出都是一个向量——因此，只需要能够在输出空间中表出就行。

 

 

 

由线性代数知识可以知道，一个向量能够被线性表出只需要基向量组能够张成空间即可，从而——问题就被转化为了怎么获取满秩的基向量并且得到对应的系数。其中，对于前者，文章证明了对于非对称的几何图这样的基向量必然存在；而对于后者，文章则采用了一种巧妙的转化。

 

近期GWL-test 系列工作开始提供一个视角：如果将“几何图等变建模”转化为“图同构可区分性问题”，则一个不变网络是完备的当且仅当其能够区分任意两个不几何同构的图。

 

 

 

与拓扑图同构问题不同的是，几何图同构问题是一个存在多项式解法的问题。通过四点定位原理，可以将坐标转化为到四个参考节点的距离，从而将需要特殊处理的等变量（坐标）转化为易于处理的不变量（距离向量）。将两个几何图按该方法处理成距离向量的集合就可以进行任意不同构几何图的区分。

 

 

 

但是，在真正神经网络建模中，需要处理单独的几何图，因此我们引入标准型（Canonical Form）的定义：

 

 

 

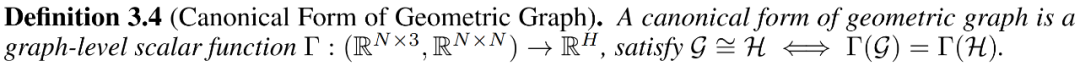
为了构造标准型，文章进一步引入Deep Set的进行处理，最后利用多层感知机（MLP）的万能逼近性就可以实现完备标量函数的学习。特别地，为了避免便利四个参考节点带来的复杂度，文章采用了类似FastEGNN的方式进行虚拟节点的学习，从而大大提升了模型的效率。

 

 

 

基于此，文章在现有的EGNN与TFN模型上进行设计，并且采用全局虚拟节点和局部虚拟节点进行设计，具体模型形式如下：

 

 

 

 

 

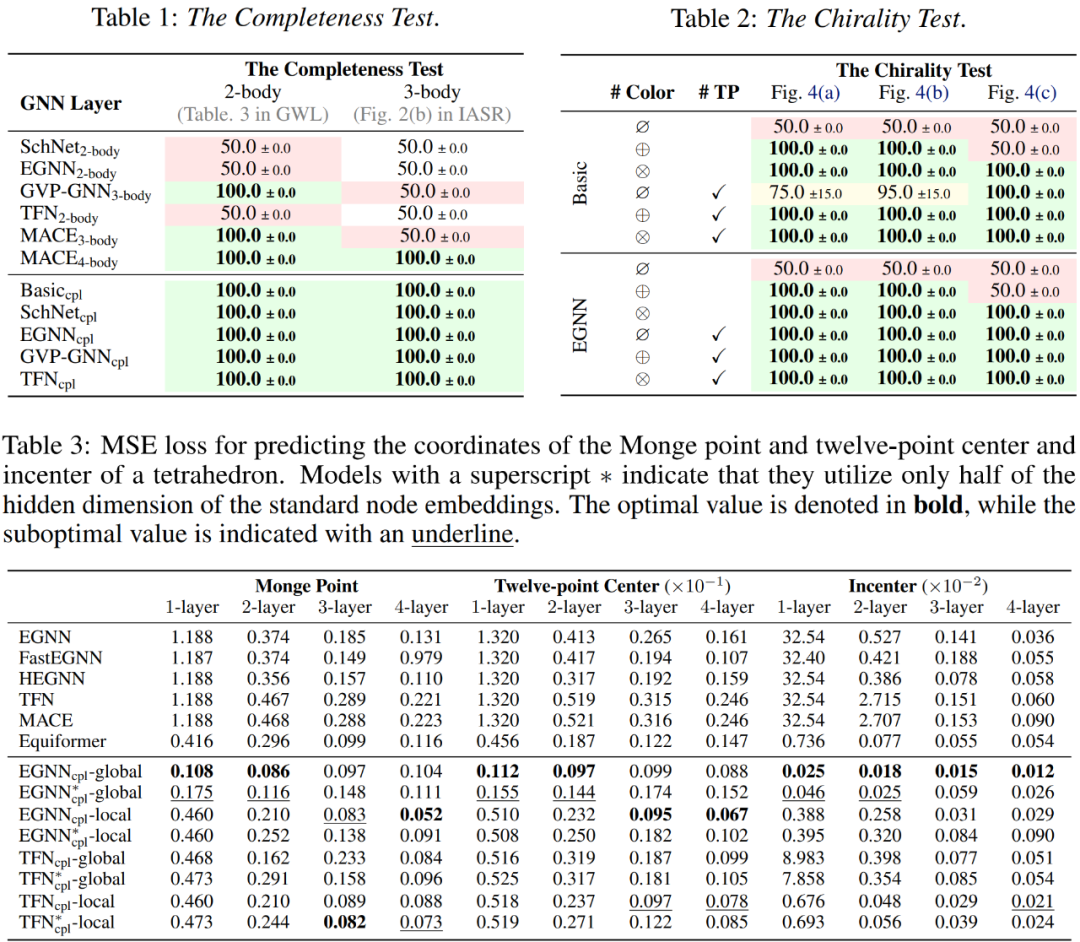
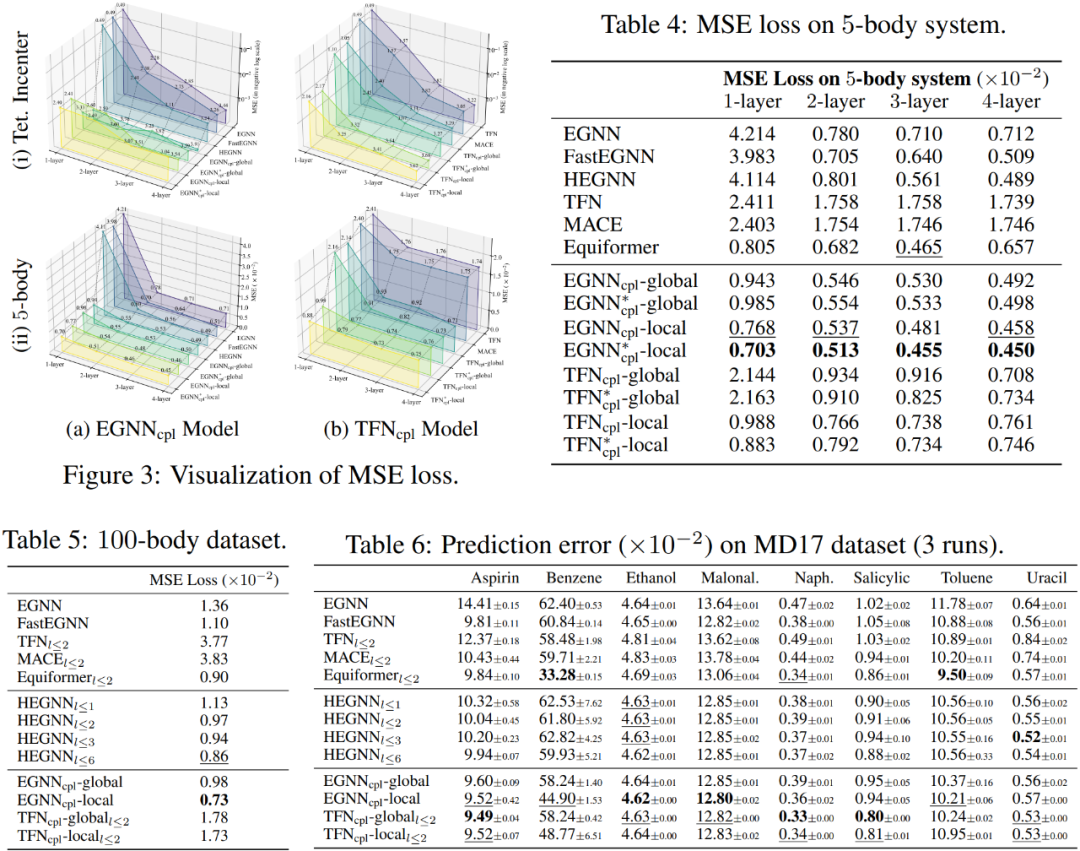
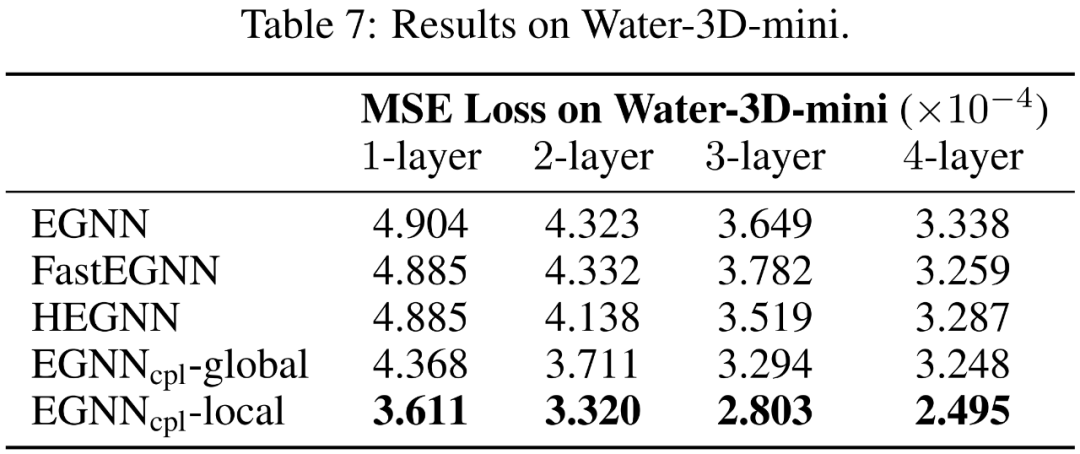
文章在多个实验上进行了测试，包括表达能力测试（GWL-test、IASR-test、手性结构区分测试）、四面体中心预测、N-body预测、MD-17动力学预测、Water-3D-mini动力学预测等不同种类不同规模的数据集，均较基线模型取得显著改进。