SLAM文献之-Embedding Manifold Structures into Kalman Filters(1)
误差状态卡尔曼滤波(Error-state Kalman filter, ESKF)是一种优雅且高效的滤波技术,适用于在流形上运行的机器人系统。然而,要为某个特定机器人系统实现 ESKF,通常需要通过在原始状态与误差状态之间切换,逐步推导滤波器的每一步,这一过程既繁琐又容易出错。为了避免这种重复的推导,本文提出了一种适用于流形上的误差状态卡尔曼滤波器的通用符号表示方法。通过利用⊟⊞操作,并在各自的
摘要
误差状态卡尔曼滤波(Error-state Kalman filter, ESKF)是一种优雅且高效的滤波技术,适用于在流形上运行的机器人系统。然而,要为某个特定机器人系统实现 ESKF,通常需要通过在原始状态与误差状态之间切换,逐步推导滤波器的每一步,这一过程既繁琐又容易出错。为了避免这种重复的推导,本文提出了一种适用于流形上的误差状态卡尔曼滤波器的通用符号表示方法。
通过利用 ⊟ \boxminus ⊟/ ⊞ \boxplus ⊞ 操作,并在各自的流形上进一步定义 ⊕ \oplus ⊕ 操作,我们提出了机器人系统的规范表示(canonical representation)。这种规范形式使我们能够在卡尔曼滤波的每一步中,将流形结构与系统描述分离,从而最终构建出一个通用的、符号化的、嵌入流形的卡尔曼滤波框架。
所提出的嵌入流形的卡尔曼滤波框架的一个主要优势在于,用户只需将系统模型转换为规范形式,而无需手动进行繁琐的流形卡尔曼滤波推导。这在高维机器人系统中尤为有用,例如扩展内部状态、多重外参、或无人机群体等情况。
此外,嵌入流形的卡尔曼滤波器以 C++ 工具包的形式实现,用户只需定义系统,并根据事件(例如输入接收、测量接收)调用相应的滤波步骤(如传播、更新)。现有实现支持在流形
S = R m × S O ( 3 ) × ⋯ × S O ( 3 ) × S 2 × ⋯ × S 2 S = \mathbb{R}^m \times SO(3) \times \cdots \times SO(3) \times S^2 \times \cdots \times S^2 S=Rm×SO(3)×⋯×SO(3)×S2×⋯×S2
及其任意子流形上的全迭代卡尔曼滤波,并可在必要时扩展至其他类型的流形。
所提出的符号化卡尔曼滤波器和开发的工具包通过实现紧耦合激光-惯性导航系统进行了验证。结果表明,该工具包在滤波性能和计算效率方面均优于手工设计的实现方案。
最后,该工具包已开源,地址为 https://github.com/hku-mars/IKFoM,以帮助实践者快速部署流形上的卡尔曼滤波器。
I. 引言
一种流行的机器人滤波技术是 误差状态扩展卡尔曼滤波器(Error-State Extended Kalman Filter, ESEKF),应用于姿态估计 [1]–[3]、在线外参标定 [4, 5]、GPS/IMU 导航 [6]、视觉惯性导航 [7]–[12] 以及激光-惯性导航 [13]–[15]。
ESEKF 的基本思想是,将状态轨迹 x τ ∈ S x_\tau \in S xτ∈S 反复参数化为从当前预测状态 x τ ∣ k x_{\tau|k} xτ∣k 出发的误差状态轨迹 δ x τ ∣ k ∈ R n \delta x_{\tau|k} \in \mathbb{R}^n δxτ∣k∈Rn:
x τ = x τ ∣ k ⊞ δ x τ ∣ k . x_\tau = x_{\tau|k} \boxplus \delta x_{\tau|k}. xτ=xτ∣k⊞δxτ∣k.
然后对误差状态轨迹 δ x τ ∣ k \delta x_{\tau|k} δxτ∣k 执行普通扩展卡尔曼滤波,用以更新误差状态,并将更新后的误差状态加回到流形上的原始状态中。由于误差较小,可以使用最小参数化(例如旋转轴与欧拉角),而无需担心奇异性问题(见图 1)。
此外,与其他技术(如无迹卡尔曼滤波 UKF)相比,扩展卡尔曼滤波的效率更高。凭借精度、稳定性和效率上的优势,ESEKF 为非线性机器人系统提供了一个优雅的卡尔曼滤波框架。
尽管具有这些优势,但为特定机器人系统部署 ESEKF 通常比普通 EKF 更困难。由于缺乏流形上系统的规范表示,现有 ESEKF 通常是逐案例设计的,并且通常要求用户充分理解其底层原理(例如在原始状态与误差状态之间切换),并为定制系统手动从头推导每一步(例如传播、更新、重置)。虽然这看似只是一个记录问题,但在实际操作中往往特别繁琐且容易出错,尤其是对于高维系统,例如机器人群体、带扩展内部状态的系统 [16] 或多个外参的系统 [17]。
除了系统维度外,当误差状态与迭代耦合时(例如迭代误差状态卡尔曼滤波器 Iterated ESEKF),手工推导的难度也会迅速增加。近年来,这种方法在视觉惯性导航 [11] 和激光-惯性导航 [14, 15] 中得到了更多应用,以减轻扩展卡尔曼滤波中的线性化误差 [18, 19]。
本文通过将流形结构嵌入卡尔曼滤波框架来解决上述问题。具体来说,我们的主要贡献如下:
-
我们提出了离散时间下机器人系统的规范化通用表示:
x k + 1 = x k ⊕ ( Δ t f ( x k , w k ) ) ; x_{k+1} = x_k \oplus \left( \Delta t f(x_k, w_k) \right); xk+1=xk⊕(Δtf(xk,wk));
-
基于规范系统表示,我们展示了流形特定结构可以与卡尔曼滤波每一步中的系统特定描述很好地分离,从而能够将流形结构嵌入卡尔曼滤波器中。我们进一步推导出一个完全迭代、符号化的误差状态卡尔曼滤波器,称为 IKFoM,基于规范系统表示;
-
我们将流形结构嵌入所推导的迭代卡尔曼滤波器,并开发了一个开源 C++ 工具包。其主要优势在于隐藏所有卡尔曼滤波推导和流形特定操作,用户只需提供系统特定描述,并在运行时调用相应的滤波步骤(例如传播、更新);
-
我们使用紧耦合激光-惯性导航系统以及多个真实数据集验证了我们的公式与实现。
II. 相关工作
卡尔曼滤波及其变体是机器人状态估计中非常有效的技术。然而,卡尔曼滤波在欧几里得空间 R n \mathbb{R}^n Rn 的状态空间中运行,而机器人系统的状态通常位于流形上(例如旋转群 S O ( 3 ) SO(3) SO(3))。为了克服这种差异,可以使用最小维度的状态参数化 [20]。
不幸的是,这种最小参数化存在奇异性。例如,SO(3) 的欧拉角表示在第二旋转轴 ±90° 时会出现奇异性,而轴-角表示在 180° 旋转时会出现奇异性 [21]。解决奇异性的办法有几种:要么避免状态空间中的这些部分(如阿波罗登月舱 [22] 所做),要么在不同的参数化顺序之间切换,每种顺序在状态空间的不同区域表现出奇异性。
另一种解决奇异性的方法是使用冗余参数表示系统状态(即过参数化)。例如,单位四元数常用于表示 SO(3) 上的旋转。然而,过参数化会将问题从系统表示转移到滤波算法:将过参数化状态视作欧几里得空间的普通向量,并应用卡尔曼滤波(或其变体),会导致传播后的状态不再位于流形上(即单位四元数约束 q T q = 1 q^T q = 1 qTq=1 被破坏)。
一种确保传播状态保持在流形上的临时方法是归一化。由于归一化对状态施加了约束,传播协方差也应相应调整。例如,单位四元数 q q q 满足 q T q = 1 q^T q = 1 qTq=1,则误差需满足 q T δ q = 0 q^T \delta q = 0 qTδq=0,意味着沿 q q q 方向的误差为零,相应的协方差也应调整为零 [23]。因此,调整后的协方差传播是奇异的。尽管只要创新协方差保持正定,卡尔曼滤波仍可工作,但未知该现象是否会引起进一步问题,例如零不确定性方向在非线性更新后可能导致其他方向的过度自信 [24]。
另一种解释归一化的方法是,将 1 视为 q T q q^T q qTq 的观测值,从而需要向系统中添加一个非线性测量 h ( q ) = q T q h(q) = q^T q h(q)=qTq。增强的测量将用于在卡尔曼滤波框架中更新协方差。这种方法在一阶近似下与前述方法等价(将 1 视为 q T q q^T q qTq 的观测值等价于将 0 视为 q T δ q q^T \delta q qTδq 的观测值),因此也存在相同的问题。
一种更优雅的方法是将原始系统(位于流形上)转换到等效误差空间(即切空间),该误差空间定义为真实状态与最近预测状态的差。由于当卡尔曼滤波收敛时误差很小,可以使用最小参数集(例如轴-角)安全参数化而不会发生奇异性。然后使用普通 EKF 更新最小参数化的误差状态,最终将其加回流形上的原始状态。这种间接更新状态估计的方法有不同的名称,例如 “误差状态” EKF (ESEKF) [6]、间接 EKF [2] 或乘法 EKF [1]。ESEKF 为将滤波技术融入流形系统提供了一种优雅的方法,并已广泛应用于各种机器人应用 [1]–[10, 12, 13]。
为了更好地描述流形上的原始状态与误差状态之间的关系,[25] 引入了 ⊞ / ⊟ \boxplus / \boxminus ⊞/⊟ 操作,并被无迹卡尔曼滤波 [24, 26] 以及最近的迭代卡尔曼滤波 [11, 14, 15] 广泛采用。这些 ⊞ / ⊟ \boxplus / \boxminus ⊞/⊟ 操作 也被广泛应用于基于流形的优化 [27, 28],例如标定 [29]、图优化 SLAM [30] 和参数识别 [31]。
本文关注于为自然位于流形上的机器人系统推导通用且符号化的卡尔曼滤波框架。我们提出了机器人系统的 规范表示,并基于此推导出一个完全迭代、符号化的卡尔曼滤波器框架。对于研究较多的特殊正交群 S O ( 3 ) SO(3) SO(3),我们的工作最终得到的卡尔曼滤波器与特定系统的结果 [1]–[10, 12, 13] 几乎相同(取决于离散化精度),但统一到一个规范形式。此外,我们的工作为引入较少研究的新型流形结构提供了一种通用方法,例如用于建模视觉地标方位向量的二维球面 S 2 S^2 S2 [11]。
本文余下部分安排如下:
- 第 III 节介绍 ⊞ / ⊟ \boxplus / \boxminus ⊞/⊟和 ⊕ \oplus ⊕ 操作;
- 第 IV 节介绍机器人系统的 规范表示;
- 第 V 节基于规范表示推导完全迭代、符号化的卡尔曼滤波器;
- 第 VI 节实现符号化误差状态迭代卡尔曼滤波器的 C++ 工具包;
- 第 VII 节给出实验结果;
- 第 VIII 节总结全文。
III.流形上的操作 (OPERATIONS ON MANIFOLDS)
流行空间相关知识可以参考:SLAM文献之A micro Lie theory for state estimation in robotic(1)
A. ⊟ \boxminus ⊟ \ ⊞ \boxplus ⊞ 和 ⊕ \oplus ⊕运算
设 S S S 是机器人所处的一个 n n n-维流形( n n n-manifold),则 S S S 在局部与切空间 R n \mathbb{R}^n Rn 同胚(locally homeomorphic)。设在 x ∈ S x \in S x∈S 处的局部映射记为
S ϕ x : S → R n {}^{S}\phi_x : S \rightarrow \mathbb{R}^n Sϕx:S→Rn
其逆映射为
S ϕ x − 1 . {}^{S}\phi_x^{-1}. Sϕx−1.
进一步假设该映射以 x x x 为中心(即 S ϕ x ( x ) = 0 {}^{S}\phi_x(x) = 0 Sϕx(x)=0 )。
参考文献 [25],我们通过两个算子 ⊞ S \boxplus_S ⊞S(“boxplus”)和 ⊟ S \boxminus_S ⊟S(“boxminus”)在 S S S 的局部邻域与 R n \mathbb{R}^n Rn 之间建立一个双射映射(bijective map):
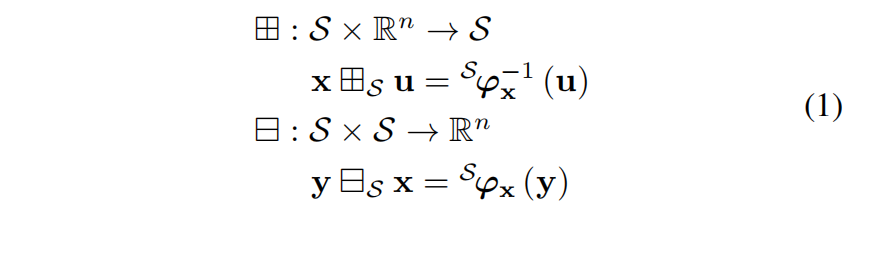
可以证明,
x ⊞ S ( y ⊟ S x ) = y x \boxplus_S ( y \boxminus_S x ) = y x⊞S(y⊟Sx)=y
以及
( x ⊞ S u ) ⊟ S x = u , ∀ x , y ∈ S , u ∈ R n . (x \boxplus_S u) \boxminus_S x = u, \quad \forall x, y \in S, u \in \mathbb{R}^n. (x⊞Su)⊟Sx=u,∀x,y∈S,u∈Rn.
对 y = x ⊞ S u y = x \boxplus_S u y=x⊞Su 的物理解释是:将一个小扰动 u ∈ R n u \in \mathbb{R}^n u∈Rn 加到 x ∈ S x \in S x∈S 上,如图 2 所示。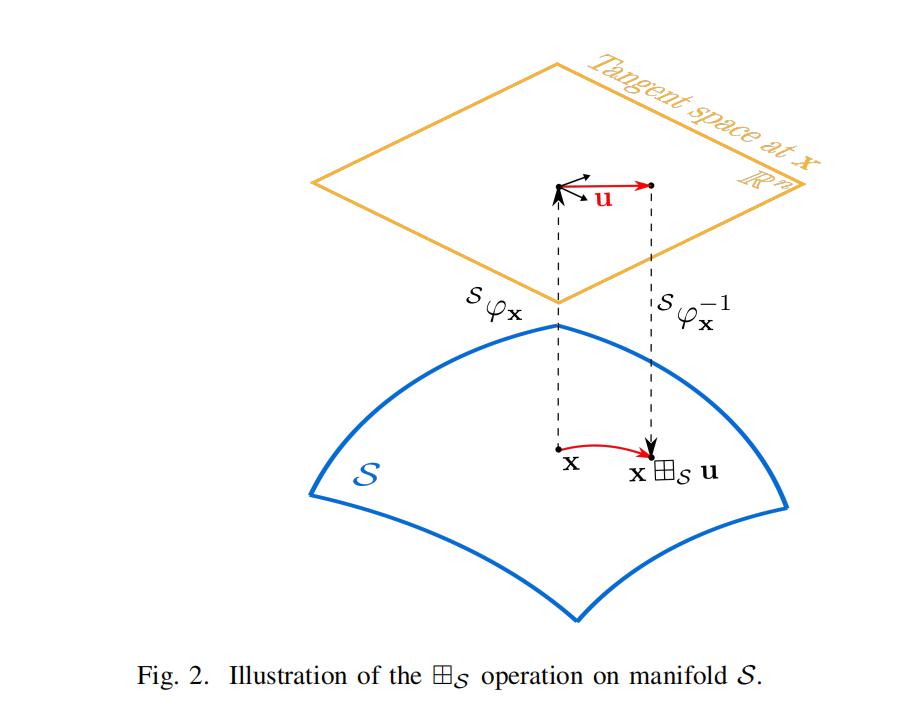
而逆运算 u = y ⊟ S x u = y \boxminus_S x u=y⊟Sx 则确定了这样一个扰动 u u u,使得当它通过 ⊞ S \boxplus_S ⊞S 运算添加到 x x x 上时,能够得到 y ∈ S y \in S y∈S。
这两个算子为流形(manifold)这种全局结构复杂的空间提供了一个局部的、向量化(vectorized)的视角。
特别地,当 S S S 是一个李群(例如 R n \mathbb{R}^n Rn、 S O ( 3 ) SO(3) SO(3)、 S E ( 3 ) SE(3) SE(3))时,局部映射 S ϕ x ( ⋅ ) S\phi_x(\cdot) Sϕx(⋅) 可简化为:
x ⊞ S u = x ⋅ E x p ( u ) x \boxplus_S u = x \cdot \mathrm{Exp}(u) x⊞Su=x⋅Exp(u)
y ⊟ S x = L o g ( x − 1 ⋅ y ) (2) y \boxminus_S x = \mathrm{Log}(x^{-1} \cdot y) \tag{2} y⊟Sx=Log(x−1⋅y)(2)
其中, ⋅ \cdot ⋅ 是作用于 S S S 上的二元运算,使得 ( S , ⋅ ) (S, \cdot) (S,⋅) 构成一个李群; E x p ( ⋅ ) \mathrm{Exp}(\cdot) Exp(⋅) 是指数映射函数 [32];而 x − 1 x^{-1} x−1 是 x x x 的逆元,根据李群定义,逆元总是存在的。
除了 ⊞ / ⊟ \boxplus / \boxminus ⊞/⊟ 之外,我们还定义了一个二元运算 ⊕ S : S × R l → S \oplus_S : S \times \mathbb{R}^l \rightarrow S ⊕S:S×Rl→S,用于根据 R l \mathbb{R}^l Rl 中的输入来驱动 S S S 中的状态。特别地,当 S S S 是一个李群(例如 R n \mathbb{R}^n Rn, S O ( 3 ) SO(3) SO(3), S E ( 3 ) SE(3) SE(3)),并且其自然由李代数通过指数映射驱动时,二元运算 ⊕ \oplus ⊕ 会简化为 ⊞ S \boxplus_S ⊞S:
x ⊕ S v = x ⊞ S u = x ⋅ E x p ( v ) ( 即 l = n ) (3) x \oplus_S v = x \boxplus_S u = x \cdot \mathrm{Exp}(v) \quad (\text{即 } l = n) \tag{3} x⊕Sv=x⊞Su=x⋅Exp(v)(即 l=n)(3)
为了简化符号,在后续讨论中,当无歧义时,我们省略运算符 ⊞ , ⊟ , ⊕ S \boxplus, \boxminus, \oplus_S ⊞,⊟,⊕S 的下标 S S S。
B. 微分(Differentiations)
在本论文稍后第 V 节将推导的卡尔曼滤波器中,将会用到表达式
( ( x ⊞ u ) ⊕ v ) ⊟ y ((x \boxplus u) \oplus v) \boxminus y ((x⊞u)⊕v)⊟y关于 u u u 和 v v v 的偏导,其中 x , y ∈ S x, y \in S x,y∈S, u ∈ R n u \in \mathbb{R}^n u∈Rn, v ∈ R l v \in \mathbb{R}^l v∈Rl。这些偏导可以通过链式法则轻松得到,如下所示:
∂ ( ( ( x ⊞ u ) ⊕ v ) ⊟ y ) ∂ u = ∂ S ϕ y ( z ) ∂ z ∣ z = ( x ⊞ u ) ⊕ v ⋅ ∂ ( z ⊕ v ) ∂ z ∣ z = x ⊞ u ⋅ ∂ S ϕ − 1 ( z ) ∂ z ∣ z = u \frac{\partial\left(((x \boxplus u) \oplus v) \boxminus y\right)}{\partial u} \left.= \frac{\partial S\phi_y(z)}{\partial z} \right|{z = (x \boxplus u) \oplus v}\\ \cdot \left. \frac{\partial (z \oplus v)}{\partial z} \right|{z = x \boxplus u} \cdot \left. \frac{\partial S\phi^{-1}(z)}{\partial z} \right|{z = u} ∂u∂(((x⊞u)⊕v)⊟y)=∂z∂Sϕy(z) z=(x⊞u)⊕v⋅∂z∂(z⊕v) z=x⊞u⋅∂z∂Sϕ−1(z) z=u
∂ ( ( ( x ⊞ u ) ⊕ v ) ⊟ y ) ∂ v = ∂ S ϕ y ( z ) ∂ z ∣ z = ( x ⊞ u ) ⊕ v ⋅ ∂ ( ( x ⊞ u ) ⊕ z ) ∂ z ∣ z = v (4) \frac{\partial\left(((x \boxplus u) \oplus v) \boxminus y\right)}{\partial v} \left.= \frac{\partial S\phi_y(z)}{\partial z} \right|{z = (x \boxplus u) \oplus v} \cdot \\ \left. \frac{\partial\left((x \boxplus u) \oplus z\right)}{\partial z} \right|{z = v} \tag{4} ∂v∂(((x⊞u)⊕v)⊟y)=∂z∂Sϕy(z) z=(x⊞u)⊕v⋅∂z∂((x⊞u)⊕z) z=v(4)
对于某些流形(例如 S O ( 3 ) SO(3) SO(3)),直接计算
∂ ( ( ( x ⊞ u ) ⊕ v ) ⊟ y ) ∂ u \frac{\partial\left(((x \boxplus u) \oplus v) \boxminus y\right)}{\partial u} ∂u∂(((x⊞u)⊕v)⊟y)
和
∂ ( ( ( x ⊞ u ) ⊕ v ) ⊟ y ) ∂ v \frac{\partial\left(((x \boxplus u) \oplus v) \boxminus y\right)}{\partial v} ∂v∂(((x⊞u)⊕v)⊟y)
通常更加方便,而不是使用上述链式法则。
C. 实际中常见的重要流形(Important manifolds in practice)
示例 1:欧氏空间 S = R n S = \mathbb{R}^n S=Rn:
x ⊞ u = x + u x \boxplus u = x + u x⊞u=x+u
y ⊟ x = y − x y \boxminus x = y - x y⊟x=y−x
x ⊕ v = x + v x \oplus v = x + v x⊕v=x+v
∂ ( ( ( x ⊞ u ) ⊕ v ) ⊟ y ) ∂ u = I n × n \frac{\partial\left(((x \boxplus u)\oplus v)\boxminus y\right)}{\partial u} = I_{n \times n} ∂u∂(((x⊞u)⊕v)⊟y)=In×n
∂ ( ( ( x ⊞ u ) ⊕ v ) ⊟ y ) ∂ v = I n × n (5) \frac{\partial\left(((x \boxplus u)\oplus v)\boxminus y\right)}{\partial v} = I_{n \times n} \tag{5} ∂v∂(((x⊞u)⊕v)⊟y)=In×n(5)
示例 2:特殊正交群 S = S O ( 3 ) S = SO(3) S=SO(3):
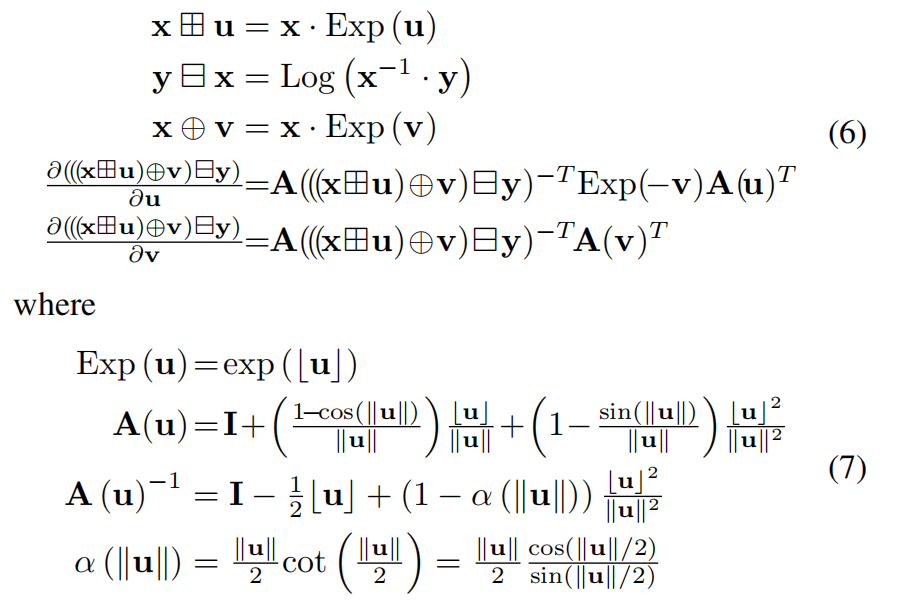
上述微分的推导过程给出了 附录 A 中的引理 1(Lemma 1)。其中,记号 u ^ \hat{u} u^(文中写作 b uc)表示与向量 u ∈ R 3 u \in \mathbb{R}^3 u∈R3 对应的反对称矩阵(skew-symmetric matrix),该矩阵用于表示与 u u u 的叉乘运算。
示例 3:特殊欧式群 S = S E ( 3 ) S = SE(3) S=SE(3)
定义如下:
- 左扰动作用
x ⊞ u = x ⋅ E x p ( u ) x \boxplus u = x \cdot \mathrm{Exp}(u) x⊞u=x⋅Exp(u)
- 右差运算
y ⊟ x = L o g ( x − 1 ⋅ y ) (8) y \boxminus x = \mathrm{Log}(x^{-1} \cdot y) \tag{8} y⊟x=Log(x−1⋅y)(8)
其中
u = [ ρ T θ T ] T ∈ R 6 , u = \begin{bmatrix} \rho^T & \theta^T \end{bmatrix}^T \in \mathbb{R}^6, u=[ρTθT]T∈R6,
E x p ( u ) [ exp ( ⌊ θ ⌋ ) ρ 0 1 ] . \mathrm{Exp}(u) \begin{bmatrix} \exp(\lfloor \theta \rfloor) & \rho \\ 0 & 1 \end{bmatrix}. Exp(u)[exp(⌊θ⌋)0ρ1].
SE(3) 的一个困难在于:其雅可比矩阵 没有闭式解(参见文献 [33])。因此在实际应用中,通常不推荐将 SE(3) 直接作为单一流形进行处理,而应将其视为复合流形:
S = S O ( 3 ) × R 3 . S = SO(3) \times \mathbb{R}^3. S=SO(3)×R3.
示例 4:二维球面 S = S 2 ( r ) S = S^2(r) S=S2(r)
二维球面定义如下:
S 2 ( r ) = x ∈ R 3 ∣ ∣ x ∣ = r , r > 0 . S^2(r)={x\in\mathbb{R}^3 \mid |x|=r,\ r>0}. S2(r)=x∈R3∣∣x∣=r, r>0.
二维球面常用于描述长度固定的矢量,例如:
- 已知幅值的重力方向向量
- 视觉特征点的方位(bearing)方向向量
(参考文献 [11])
根据图 3,定义 x ⊞ u x \boxplus u x⊞u 的一种方式是:让 x x x 沿切平面内的向量 u ∈ R 2 u\in\mathbb{R}^2 u∈R2 旋转,这样结果仍然位于球面 S 2 ( r ) S^2(r) S2(r)。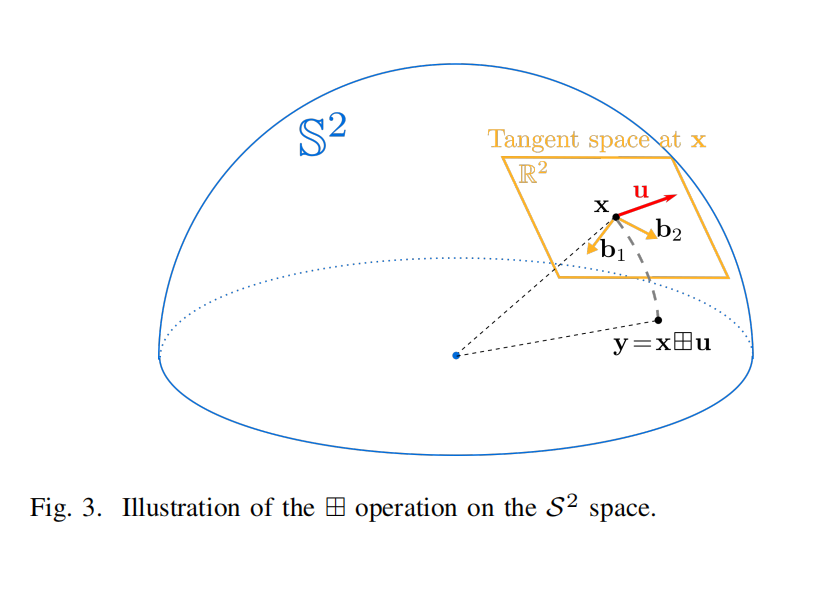
设 b 1 , b 2 b_1, b_2 b1,b2 为切平面上的两个标准正交基(orthonormal basis),回忆式 (7) 中指数映射的定义,则可写为:
x ⊞ u ≜ E x p ( [ b 1 b 2 ] u ) . x (9) x \boxplus u \triangleq \mathrm{Exp}\left( \begin{bmatrix} b_1 & b_2 \end{bmatrix} u \right){.} x \tag{9} x⊞u≜Exp([b1b2]u).x(9)
在许多机器人系统中(见第四节), S 2 ( r ) S^2(r) S2(r) 上的状态通常表示可能经历一定角运动的方向。因此,更适合的 ⊕ \oplus ⊕ 二元运算形式是使用 旋转向量 v ∈ R 3 v\in\mathbb{R}^3 v∈R3 进行旋转:
⊕ : S 2 ( r ) × R 3 → S 2 ( r ) \oplus : S^2(r) \times \mathbb{R}^3 \to S^2(r) ⊕:S2(r)×R3→S2(r)
x ⊕ v = E x p ( v ) . x . (10) x \oplus v = \mathrm{Exp}(v). x. \tag{10} x⊕v=Exp(v).x.(10)
注意: b 1 b_1 b1 和 b 2 b_2 b2 依赖于 x x x,定义矩阵
B ( x ) = [ b 1 b 2 ] ∈ R 3 × 2 . B(x)= \begin{bmatrix} b_1 & b_2 \end{bmatrix} \in \mathbb{R}^{3\times 2}. B(x)=[b1b2]∈R3×2.
于是有:
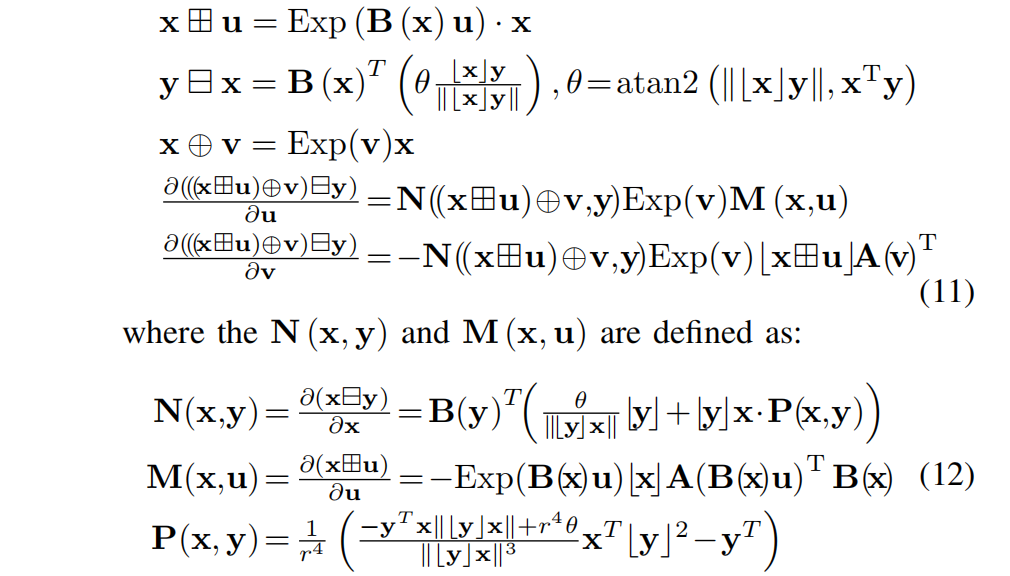
其中 A ( ⋅ ) A(\cdot) A(⋅) 的定义见公式 (7)。注意,对于所有 y ∈ S 2 y \in S^2 y∈S2,都有:
N ( y , y ) = 1 r 2 B ( y ) T ⌊ y ⌋ . N(y, y)=\frac{1}{r^2} B(y)^T \lfloor y \rfloor . N(y,y)=r21B(y)T⌊y⌋.
上述结果并未具体规定基 B ( x ) B(x) B(x) 的选取方式,只要求它必须是 x x x 的切平面上的一组正交归一基即可。因此 B ( x ) B(x) B(x) 可以任意构造,只要满足正交性条件。
例如,我们可以采用文献 [34] 中的方法(见图 4):将三个标准基向量 e i , i = 1 , 2 , 3 e_i,\ i=1,2,3 ei, i=1,2,3 中的一个沿测地线旋转到点 x x x,然后其余两个经过该旋转后的 e i e_i ei 就构成 B ( x ) B(x) B(x)。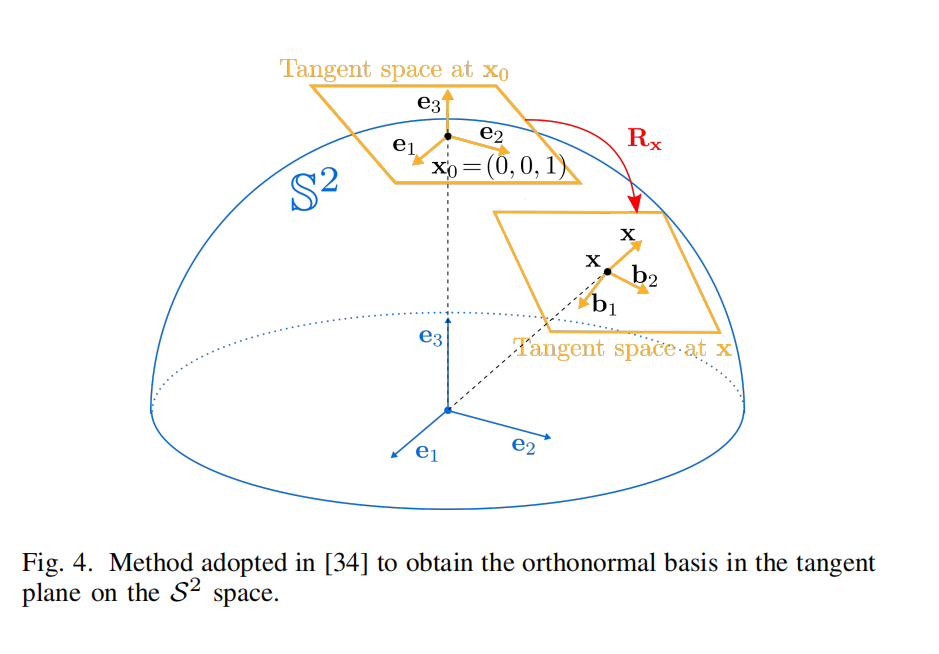
为了避免当 x = − r e i x = - r e_i x=−rei 时旋转会出现奇异情况, e i e_i ei 的选取方式为:瞬时选择与 − x -x −x 的距离最大的那一个标准基向量:
i = arg max j x T e j . i = \arg\max_j x^T e_j. i=argjmaxxTej.
定义旋转为:
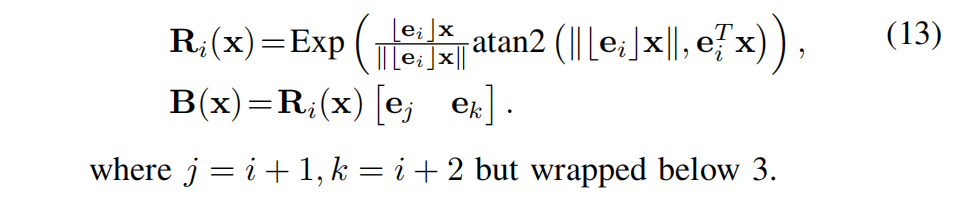
D. 复合(compound)流形上的 ⊞ \boxplus ⊞、 ⊟ \boxminus ⊟ 与 ⊕ \oplus ⊕ 操作
基于流形笛卡尔积(Cartesian product)的原理,对于由两个(或通过数学归纳法扩展为任意多个)子流形组成的复合流形,其 ⊞ \boxplus ⊞、 ⊟ \boxminus ⊟ 与 ⊕ \oplus ⊕ 操作可定义为:
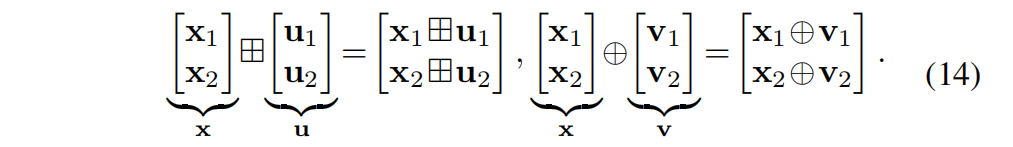
如附录 B 中的引理 2 所证明,复合流形上的偏导可写为分块对角形式:
∂ ( ( ( x ⊞ u ) ⊕ v ) ⊟ y ) ∂ u = [ ∂ ( ( ( x 1 ⊞ u 1 ) ⊕ v 1 ) ⊟ y 1 ) ∂ u 1 0 0 ∂ ( ( ( x 2 ⊞ u 2 ) ⊕ v 2 ) ⊟ y 2 ) ∂ u 2 ] , \frac{\partial\big(((x \boxplus u)\oplus v)\boxminus y\big)}{\partial u}= \begin{bmatrix} \dfrac{\partial\big(((x_1 \boxplus u_1)\oplus v_1)\boxminus y_1\big)}{\partial u_1} & 0 \ \\0 & \dfrac{\partial\big(((x_2 \boxplus u_2)\oplus v_2)\boxminus y_2\big)}{\partial u_2} \end{bmatrix}, ∂u∂(((x⊞u)⊕v)⊟y)= ∂u1∂(((x1⊞u1)⊕v1)⊟y1)00 ∂u2∂(((x2⊞u2)⊕v2)⊟y2) ,
∂ ( ( ( x ⊞ u ) ⊕ v ) ⊟ y ) ∂ v = [ ∂ ( ( ( x 1 ⊞ u 1 ) ⊕ v 1 ) ⊟ y 1 ) ∂ v 1 0 0 ∂ ( ( ( x 2 ⊞ u 2 ) ⊕ v 2 ) ⊟ y 2 ) ∂ v 2 ] . (15) \frac{\partial\big(((x \boxplus u)\oplus v)\boxminus y\big)}{\partial v}= \begin{bmatrix} \dfrac{\partial\big(((x_1 \boxplus u_1)\oplus v_1)\boxminus y_1\big)}{\partial v_1} & 0 \\ 0 & \dfrac{\partial\big(((x_2 \boxplus u_2)\oplus v_2)\boxminus y_2\big)}{\partial v_2} \end{bmatrix}.\tag{15} ∂v∂(((x⊞u)⊕v)⊟y)= ∂v1∂(((x1⊞u1)⊕v1)⊟y1)00∂v2∂(((x2⊞u2)⊕v2)⊟y2) .(15)
复合流形上的 ⊞ \boxplus ⊞、 ⊟ \boxminus ⊟ 与 ⊕ \oplus ⊕ 操作及其导数极其有用,它们使我们能够仅针对基本流形(如 S O ( 3 ) SO(3) SO(3)、 R n \mathbb{R}^n Rn、 S 2 ( r ) S^2(r) S2(r))定义这些操作及其导数,并将这些定义自动扩展到更复杂的复合流形上。
IV. 规范表示(Canonical Representation)
考虑离散时间的机器人系统,其采样周期为 Δ t \Delta t Δt,经过零阶保持(zero-order hold)离散化后,我们可将系统写成如下规范形式:
x k + 1 = x k ⊕ S ( Δ t f ( x k , u k , w k ) ) , x k ∈ S , x_{k+1} = x_k \oplus_S \left( \Delta t f(x_k, u_k, w_k) \right), \quad x_k \in S, xk+1=xk⊕S(Δtf(xk,uk,wk)),xk∈S,
z k = h ( x k , v k ) , z k ∈ M , z_k = h(x_k, v_k), \quad z_k \in M, zk=h(xk,vk),zk∈M,
w k ∼ N ( 0 , Q k ) , v k ∼ N ( 0 , R k ) . (16) w_k \sim \mathcal{N}(0, Q_k), \qquad v_k \sim \mathcal{N}(0, R_k).\tag{16} wk∼N(0,Qk),vk∼N(0,Rk).(16)
其中,测量 z k z_k zk 被假设位于维度为 m m m 的流形 M M M 上。例如在松耦合视觉惯性里程计(VIO)或激光惯性里程计(LIO)中,测量是一个位姿,因此属于 S E ( 3 ) SE(3) SE(3)。与以往工作中使用的高阶离散化方法(如 Runge–Kutta 积分)相比,零阶保持离散化的精度通常较低,但当采样周期足够小时,这种差异可以忽略不计。
接下来,我们将展示如何将不同的状态分量转化为上述规范形式 (16)。然后结合复合流形的运算性质(公式 14),通过状态分量的拼接即可得到完整的状态方程。
示例 1:欧氏空间中的向量(如位置与速度)
假设 x ∈ R n x \in \mathbb{R}^n x∈Rn,其连续系统满足:
x ˙ = f ( x , u , w ) . \dot{x} = f(x, u, w). x˙=f(x,u,w).
使用零阶保持离散化, f ( x , u , w ) f(x,u,w) f(x,u,w) 在采样周期 Δ t \Delta t Δt 内视为常量,因此:
x k + 1 = x k + ( Δ t f ( x k , u k , w k ) ) = x k ⊕ R n ( Δ t f ( x k , u k , w k ) ) . (17) x_{k+1} = x_k + \left( \Delta t f(x_k, u_k, w_k) \right) = x_k \oplus_{\mathbb{R}^n} \left( \Delta t f(x_k, u_k, w_k) \right). \tag{17} xk+1=xk+(Δtf(xk,uk,wk))=xk⊕Rn(Δtf(xk,uk,wk)).(17)
这表明欧氏空间下的 ⊕ R n \oplus_{\mathbb{R}^n} ⊕Rn 实质即为向量加法。
示例 2:全局参考系下的姿态运动学(如地球系)
设 x ∈ S O ( 3 ) x \in SO(3) x∈SO(3) 表示机体相对于全局坐标系的姿态,而 G ω {}^G\omega Gω 为机体在全局坐标系下的角速度,并假设其在一个采样周期 Δ t \Delta t Δt 内保持恒定。
连续系统:
x ˙ = [ G ω ] . x \dot{x} = [G\omega]. x x˙=[Gω].x
由此得到离散时间形式:
x k + 1 = exp ( Δ t G ω k ) . x k x_{k+1} = \exp\left(\Delta t {}^G\omega_k\right). x_k xk+1=exp(ΔtGωk).xk
又因为姿态也可写成右乘扰动形式:
x k + 1 = x k ⋅ exp ( Δ t ( x k ⊤ . G ω k ) ) = x k ⊕ S O ( 3 ) ( Δ t f ( x k , G ω k ) ) , f ( x k , G ω k ) = x k ⊤ ⋅ G ω k (18) x_{k+1} = x_k \cdot \exp\left( \Delta t (x_k^\top .{}^G\omega_k) \right) = x_k \oplus_{SO(3)} \left( \Delta t f(x_k, {}^G\omega_k) \right),\\ f(x_k, G\omega_k) = x_k^{\top} \cdot G_{\omega_k}\tag{18} xk+1=xk⋅exp(Δt(xk⊤.Gωk))=xk⊕SO(3)(Δtf(xk,Gωk)),f(xk,Gωk)=xk⊤⋅Gωk(18)
其中 f ( ⋅ ) f(\cdot) f(⋅) 为表示角速度映射到李代数的函数。
示例 3:机体坐标系下的姿态运动学
设 x ∈ S O ( 3 ) x \in SO(3) x∈SO(3) 表示机体相对于全局参考系的姿态, B ω B\omega Bω 为机体角速度,并假设其在一个采样周期 Δ t \Delta t Δt 内保持恒定。则连续系统为:
x ˙ = x ⋅ [ B ω ] ⇒ x k + 1 = x k ⋅ exp ( Δ t , B ω k ) = x k ⊕ S O ( 3 ) ( Δ t f ( B ω k ) ) , f ( B ω k ) = B ω k . (19) \dot{x} = x \cdot [{}^B\omega] \quad \Rightarrow \quad x_{k+1} = x_k \cdot \exp(\Delta t, {}^B\omega_k)\\ = x_k \oplus_{SO(3)} \big(\Delta t f({}^B\omega_k)\big), \quad f({}^B\omega_k) = {}^B\omega_k.\tag{19} x˙=x⋅[Bω]⇒xk+1=xk⋅exp(Δt,Bωk)=xk⊕SO(3)(Δtf(Bωk)),f(Bωk)=Bωk.(19)
示例 4:全局参考系下已知幅值的向量(如重力向量)
设 x ∈ S 2 ( g ) x \in S^2(g) x∈S2(g) 表示全局参考系下幅值为 g g g 的重力向量,则连续系统为:
x ˙ = 0 ⇒ x k + 1 = x k = x k ⊕ S 2 ( g ) ( Δ t f ( x k ) ) , f ( x k ) = 0. (20) \dot{x} = 0 \quad \Rightarrow \quad x_{k+1} = x_k = x_k \oplus_{S^2(g)} \big(\Delta t f(x_k)\big), \quad f(x_k) = 0.\tag{20} x˙=0⇒xk+1=xk=xk⊕S2(g)(Δtf(xk)),f(xk)=0.(20)
示例 5:机体坐标系下已知幅值的向量(如重力向量)
设 x ∈ S 2 ( g ) x \in S^2(g) x∈S2(g) 表示机体坐标系下的重力向量, B ω B\omega Bω 为机体角速度并假设在采样周期 Δ t \Delta t Δt 内保持恒定,则连续系统为:
x ˙ = − [ B ω ] x ⇒ x k + 1 = exp ( − Δ t , B ω k ) x k = x k ⊕ S 2 ( g ) ( Δ t f ( B ω k ) ) , f ( B ω k ) = − B ω k . (21) \dot{x} = -[{}^B\omega] x \quad \Rightarrow \quad x_{k+1} = \exp(-\Delta t, {}^B\omega_k) x_k\\ = x_k \oplus_{S^2(g)} \big(\Delta t f({}^B\omega_k)\big), \quad f({}^B\omega_k) = -{}^B\omega_k.\tag{21} x˙=−[Bω]x⇒xk+1=exp(−Δt,Bωk)xk=xk⊕S2(g)(Δtf(Bωk)),f(Bωk)=−Bωk.(21)
示例 6:视觉特征的方位-距离参数化
设 x ∈ S 2 ( 1 ) x \in S^2(1) x∈S2(1) 为视觉特征的方位向量, d ( ρ ) ∈ R d(\rho) \in \mathbb{R} d(ρ)∈R 为深度(参数为 ρ \rho ρ), G R C {}^G R_C GRC, G p C {}^G p_C GpC 分别为相机的姿态和位置,则全局参考系下的视觉特征位置为:
G R C ( x d ( ρ ) ) + G p C , G R_C \big(x d(\rho)\big) + {}^G p_C, GRC(xd(ρ))+GpC,
该量在时间上保持不变。
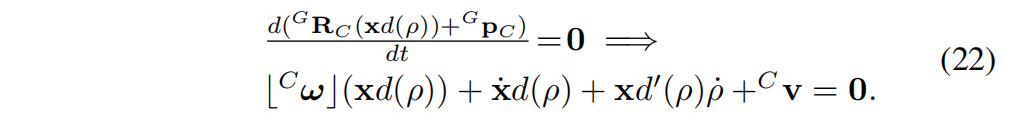
将公式 (22) 左乘 x T x^T xT 并利用 x T x ˙ = 0 x^T \dot{x} = 0 xTx˙=0 可得:
ρ ˙ = − x T ⋅ C v / d 0 ( ρ ) . \dot{\rho} = - x^T \cdot {}^C v / d_0(\rho). ρ˙=−xT⋅Cv/d0(ρ).
将此结果代入公式 (22) 可得到: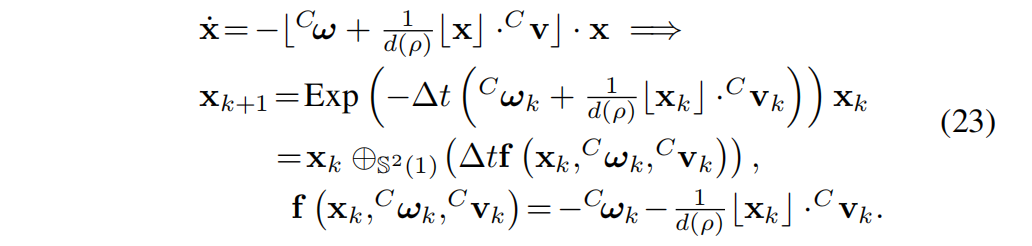
由于零阶保持(zero-order hold)假设,令
C ω + d ( 1 ρ ) b x ⋅ C v C \omega + d\left(\frac{1}{\rho}\right) \mathbf{b}x \cdot C v Cω+d(ρ1)bx⋅Cv
在一个采样周期 Δ t \Delta t Δt 内保持不变。

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献17条内容
已为社区贡献17条内容






所有评论(0)