六自由度机械臂+RRT路径轨迹规划算法仿真 [1]描述：将RRT路径轨迹规划算法与机械臂进行结合，且机械臂为六自由度机械臂 [2]程序中障碍物，起始点坐标均可修改 [3]包括：六关节曲线、关节速度曲线、加速度曲线 程序附带详细中文注释，快速学习RRT＋机械臂，事半功倍

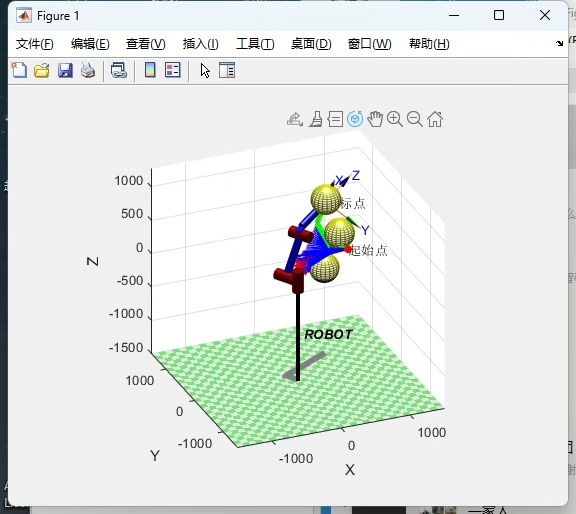
在机器人领域，六自由度机械臂就像一个全能选手，凭借其六个关节的灵活运动，可以完成各种复杂的任务。而RRT（快速探索随机树）路径轨迹规划算法，如同为这个全能选手指明方向的智慧大脑，帮助机械臂在复杂环境中找到合适的运动路径。今天就来聊聊如何将二者结合进行仿真。

算法与机械臂结合的奇妙之处

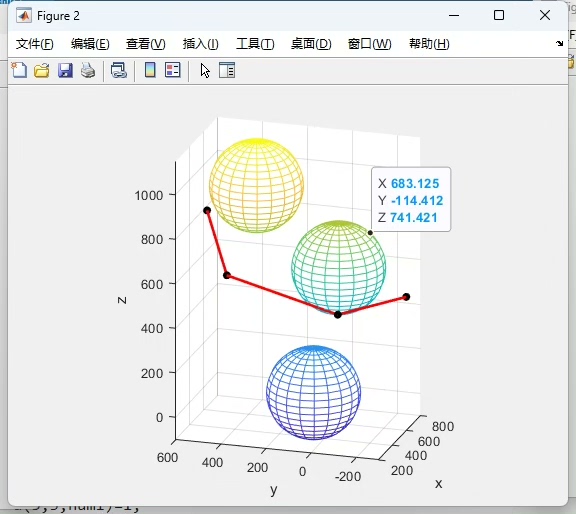
六自由度机械臂，拥有沿三个坐标轴的平移和绕三个坐标轴的旋转运动能力，这使得它在空间操作上具有极大的灵活性。但当面对复杂环境中有障碍物的情况时，如何让它从起始点顺利到达目标点而不发生碰撞呢？这就是RRT算法大显身手的地方。

RRT算法通过在状态空间中随机采样点，并逐步构建一棵树，从起始点开始，像触手一样不断向周围探索，直到找到目标点或者确定不存在可行路径。把这个算法应用到六自由度机械臂上，就如同赋予了机械臂一个智能导航系统，让它能在复杂环境中安全穿梭。

可修改的程序要素：障碍物与起始点坐标

在实际编程实现中，我们需要让程序具备一定的灵活性，以便适应不同的场景需求。这里就涉及到障碍物和起始点坐标的可修改性。

以下是一段简单的Python示例代码（假设使用的是基于Python的仿真库，实际可能会根据具体库进行调整）：

# 定义障碍物的坐标
obstacle_x = 0.5
obstacle_y = 0.5
obstacle_z = 0.5

# 定义起始点坐标
start_x = 0
start_y = 0
start_z = 0

# 这里可以根据实际需求修改上述坐标值，以适应不同场景

通过这样简单的变量定义方式，只要在程序运行前修改这些变量的值，就能轻松改变障碍物的位置和机械臂的起始点，从而模拟不同的环境和任务初始条件。

关键曲线：关节、速度与加速度曲线

1. 六关节曲线

六关节曲线描述了机械臂各个关节在运动过程中的角度变化情况。它反映了机械臂每个关节是如何协同工作，以实现从起始点到目标点的运动。

在代码实现上，可能会有类似下面这样的片段来计算和绘制关节曲线（假设使用matplotlib库进行绘图）：

import matplotlib.pyplot as plt
import numpy as np

# 假设已经计算得到关节角度随时间的变化值，存储在joint_angles列表中
# 这里为了示例，简单生成一些随机数据模拟关节角度变化
time = np.linspace(0, 10, 100)
joint_angles = [np.sin(t) for t in time]

plt.plot(time, joint_angles)
plt.xlabel('时间 (s)')
plt.ylabel('关节角度 (度)')
plt.title('六关节曲线')
plt.show()

在这段代码中，我们首先导入了绘图需要的库matplotlib.pyplot和数值计算库numpy。然后通过np.linspace函数生成了一个时间序列，接着模拟生成了关节角度随时间的变化值（这里简单用正弦函数模拟），最后使用plt.plot绘制曲线，并添加了坐标轴标签和标题，通过plt.show显示图形。

1. 关节速度曲线

关节速度曲线展示了关节角度随时间变化的速率。它对于评估机械臂运动的平稳性和效率非常重要。

计算关节速度可以基于关节角度的数值微分。以下是一个简单的示例代码来计算和绘制关节速度曲线：

# 计算关节速度，这里简单使用相邻点的差分近似速度
joint_velocities = [(joint_angles[i+1] - joint_angles[i]) / (time[1] - time[0]) for i in range(len(time)-1)]

plt.plot(time[:-1], joint_velocities)
plt.xlabel('时间 (s)')
plt.ylabel('关节速度 (度/秒)')
plt.title('关节速度曲线')
plt.show()

在这个代码片段中，我们通过对关节角度数据进行相邻点的差分，并除以时间间隔，近似得到了关节速度。然后同样使用matplotlib绘制了关节速度随时间变化的曲线。

1. 加速度曲线

加速度曲线则反映了关节速度变化的快慢。它对于了解机械臂在运动过程中的动态特性至关重要，比如是否存在过于剧烈的速度变化导致机械臂振动等问题。

计算加速度与计算速度类似，基于速度的数值微分。代码示例如下：

# 计算关节加速度，同样使用相邻点的差分近似加速度
joint_accelerations = [(joint_velocities[i+1] - joint_velocities[i]) / (time[1] - time[0]) for i in range(len(time)-2)]

plt.plot(time[:-2], joint_accelerations)
plt.xlabel('时间 (s)')
plt.ylabel('关节加速度 (度/秒²)')
plt.title('关节加速度曲线')
plt.show()

这段代码通过对关节速度数据进行相邻点差分并除以时间间隔，近似得到关节加速度，最后绘制出加速度随时间变化的曲线。

详细中文注释：快速学习的利器

程序附带详细中文注释是极其重要的，它就像一位无声的老师，引导初学者快速理解代码的逻辑和功能。

比如在上述计算关节曲线的代码中，每一行注释都清晰地说明了代码的作用：

# 导入绘图需要的库matplotlib.pyplot，一般简写成plt
import matplotlib.pyplot as plt
# 导入数值计算库numpy，一般简写成np
import numpy as np

# 假设已经计算得到关节角度随时间的变化值，存储在joint_angles列表中
# 这里为了示例，简单生成一些随机数据模拟关节角度变化
# 使用np.linspace函数生成从0到10，共100个点的时间序列
time = np.linspace(0, 10, 100)
# 简单用正弦函数模拟关节角度随时间的变化
joint_angles = [np.sin(t) for t in time]

# 使用plt.plot绘制关节角度随时间变化的曲线
plt.plot(time, joint_angles)
# 设置x轴标签为'时间 (s)'
plt.xlabel('时间 (s)')
# 设置y轴标签为'关节角度 (度)'
plt.ylabel('关节角度 (度)')
# 设置图形标题为'六关节曲线'
plt.title('六关节曲线')
# 显示绘制的图形
plt.show()

这样详细的注释，无论是对于刚接触六自由度机械臂和RRT算法的新手，还是想要快速理解代码实现细节的开发者，都能起到事半功倍的学习效果。

通过将RRT路径轨迹规划算法与六自由度机械臂相结合，并深入分析关节曲线、速度曲线和加速度曲线，同时借助详细注释的代码，我们不仅能更好地理解机械臂在复杂环境中的运动规划，还能为实际应用中的优化和改进提供有力的支持。希望大家在这个领域探索出更多有趣的成果！