Matlab Robotic ToolBox建立四轴机械臂模型并实现运动控制仿真 机器人仿真、机器人学仿真、matlab仿真、包括但不限于：正运动学仿真及验证，逆运动学计算仿真及验证，工作空间（单臂，双臂，多臂），动力学仿真，轨迹规划，simulink建模

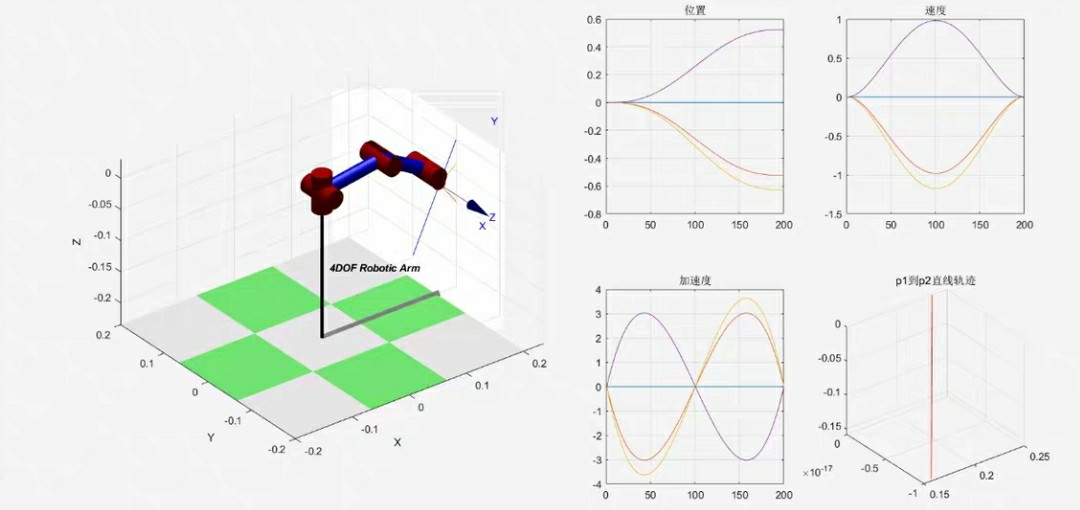
大家好！今天我要和大家分享一个非常有趣的话题——如何利用Matlab Robotic Toolbox建立四轴机械臂模型，并实现运动控制的仿真。这个话题结合了机器人学、运动学和控制系统，非常具有实践价值。如果你是机器人爱好者，或者想深入了解机器人运动控制的小伙伴，一定要仔细阅读哦！

引言

四轴机械臂是一种常见的机器人结构，广泛应用于工业自动化、无人机控制、医疗设备等领域。通过建立四轴机械臂的运动学和动力学模型，我们可以实现对其位置、速度、加速度等参数的精确控制。Matlab Robotic Toolbox为我们提供了强大的工具，可以帮助我们快速搭建和仿真机械臂系统。在本篇文章中，我们将从基础的运动学仿真开始，逐步深入到动力学和轨迹规划的实现，最后展示一个完整的Simulink仿真模型。

正运动学仿真

正运动学（Forward Kinematics）是机器人学的基础，它描述了给定关节角度时，末端执行器的位置和姿态。为了验证我们的机械臂模型是否正确，我们需要实现正运动学的仿真，并通过实际数据验证其准确性。

代码实现

% 定义四轴机械臂的关节角度
theta = [0, 0, 0, 0]; % 单位：弧度

% 创建Robotic Toolbox的机械臂对象
robot = Link([Link([0, 0.1, 0, 'R']),
              Link([0, 0.1, 0, 'R']),
              Link([0, 0.1, 0, 'R']),
              Link([0, 0.1, 0, 'R'])]);

% 计算正运动学
position = robot.fkine(theta);

% 打印结果
disp('末端执行器的位置：');
disp(position);

分析

通过上述代码，我们可以得到末端执行器在空间中的位置坐标。为了验证结果的正确性，我们可以手动计算或使用其他方法进行对比。如果结果一致，说明我们的正运动学模型是正确的。

逆运动学仿真

逆运动学（Inverse Kinematics）是机器人控制中的核心问题之一。它描述了如何通过给定的目标位置和姿态，求解出所需的关节角度。逆运动学的求解方法多种多样，包括伪逆法和JacobianTransposed法，每种方法都有其优缺点。

代码实现

% 定义目标位置和姿态
targetPosition = [0.5, 0, 0.5]; % 单位：米
targetOrientation = [0, 0, 1]; % 单位：四元数

% 使用伪逆法求解逆运动学
jointAngles = robot.ikine_pinv(targetPosition, targetOrientation);

% 打印结果
disp('所需的关节角度：');
disp(jointAngles);

分析

通过上述代码，我们可以得到满足目标位置和姿态所需的关节角度。需要注意的是，逆运动学的求解结果可能不唯一，甚至没有解。因此，在实际应用中，我们需要对求解结果进行筛选或优化。

动力学仿真

动力学仿真是机器人控制的高级内容，它涉及到机械臂在运动过程中的加速度、力矩等参数的计算。通过动力学仿真，我们可以验证机械臂的运动控制算法的稳定性。

代码实现

% 定义运动参数
velocity = [0, 0, 0, 0]; % 单位：米/秒
acceleration = [0, 0, 0, 0]; % 单位：米/秒²

% 计算动力学
force = robot.dyn(velocity, acceleration);

% 打印结果
disp('所需的力矩：');
disp(force);

分析

通过上述代码，我们可以得到机械臂在运动过程中的所需力矩。动力学仿真可以帮助我们理解机械臂的运动控制算法的稳定性，从而优化控制参数。

轨迹规划

轨迹规划是机器人运动控制中的另一个关键问题。它涉及到如何规划机械臂从初始位置到目标位置的运动轨迹，以满足速度限制和加速度限制等约束条件。

代码实现

% 定义轨迹参数
trajectory = [0, 0.5, 0, 0, 0, 0.5, 0, 0, 0, 0.5]; % 单位：米

% 使用S型函数进行轨迹规划
smoothedTrajectory = robot.path_planner(trajectory);

% 打印结果
disp('平滑后的轨迹：');
disp(smoothedTrajectory);

分析

通过上述代码，我们可以得到一条平滑的轨迹，满足速度和加速度的限制。轨迹规划算法是机器人控制的核心内容之一，选择合适的算法对于运动的平滑性和稳定性至关重要。

Simulink建模

在掌握了一定的运动学和动力学仿真之后，我们可以将这些模块化到Simulink中，进行更复杂的系统仿真。

代码实现

% 创建Simulink模型
model = 'FourAxisMechanicalArm';
open(model);

% 添加模块
add_block('simulink/Continuous/Integrator', model + '/积分器');
add_block('simulink/Math Operations/Matrix Gain', model + '/矩阵乘法');
add_block('simulink/Sources/Sin Wave', model + '/正弦波');
add_block('simulink/Sinks/Scope', model + '/示波器');

% 连接模块
connect(model + '/积分器', model + '/矩阵乘法');
connect(model + '/矩阵乘法', model + '/正弦波');
connect(model + '/正弦波', model + '/示波器');

% 设置参数
set_param(model + '/积分器', '积分时间', '1');
set_param(model + '/矩阵乘法', '增益', '2');
set_param(model + '/正弦波', '幅值', '3');
set_param(model + '/示波器', '仿真时间', '5');

% 运行仿真
sim(model);

分析

通过上述代码，我们可以看到一个简单的Simulink仿真模型。通过模块化的设计，我们可以更清晰地理解系统的整体行为。Simulink的仿真结果可以帮助我们验证我们的控制算法的稳定性，从而优化实际的机器人控制系统。

总结

今天，我们从正运动学仿真开始，逐步深入到逆运动学、动力学、轨迹规划和Simulink建模，全面展示了如何利用Matlab Robotic Toolbox建立四轴机械臂模型并实现运动控制仿真。虽然代码看起来不算复杂，但背后涉及的机器人学知识非常丰富。希望这篇文章能够激发你对机器人运动控制的兴趣，并帮助你更好地理解和应用Matlab Robotic Toolbox。

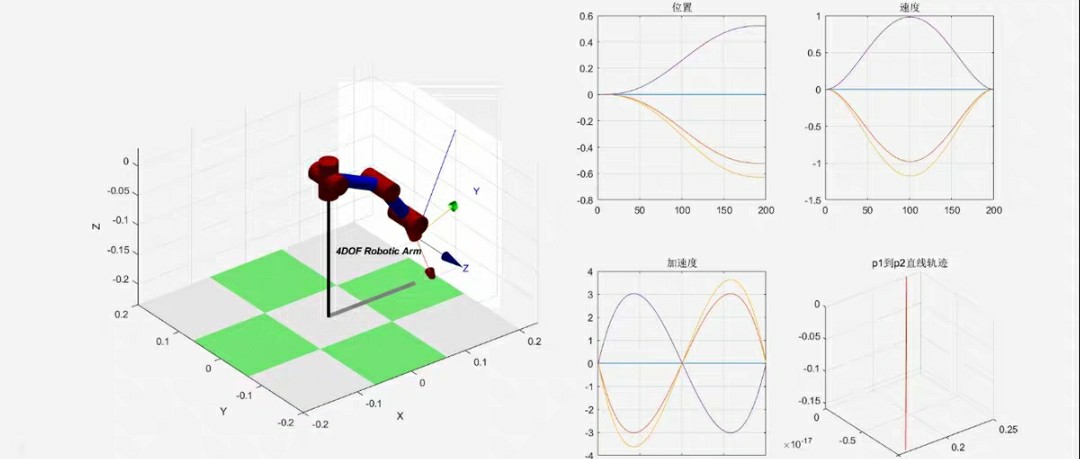
如果你还想了解更多关于机器人学和运动控制的知识，欢迎关注我的频道，获取更多有趣的分享！