HNU算法设计与分析实验四(安全专业)
5-18 世界名画陈列馆问题(不重复监视)
问题描述
世界名画陈列馆由m×n个排列成矩形阵列的陈列室组成。为了防止名画被盗,需要在陈列室中设置警卫机器人哨位。除了监视所在的陈列室,每个警卫机器人还可以监视与它所在的陈列室相邻的上、下、左、右4个陈列室。试设计一个安排警卫机器人哨位的算法,使名画陈列馆中每个陈列室都在警卫机器人的监视下,并且要求每个陈列室仅受一个警卫机器人监视,且所用的警卫机器人数最少。
算法设计
设计一个算法,计算警卫机器人的最佳哨位安排方案,使名画陈列馆中每个陈列室都仅受一个警卫机器人监视。且所用的警卫机器人数最少。
数据输入
由文件input.txt给出输入数据。第1行有2个正整数m和n(1<m,n<20)。
结果输出
将计算的警卫机器人数及其最佳哨位安排输出到文件output.txt。文件的第1行是警卫机器人数;接下来的m行中每行n个数,0表示无哨位,1表示哨位。如果不存在满足要求的哨位安排方案,则输出“NoSolution!”。
输入文件示例 输出文件示例
input.txt output.txt
4 4 4
0010
1000
0001
0100
算法实现与思路分析
算法选择
暴力搜索需枚举2^mn 种组合(每个位置有警卫和无警卫两种选择),复杂度过高了,这种情况不考虑。
本题采用DFS求解,但是由于我们需要得到的是最少的警卫数量,如果直接用DFS遍历,最开始的计算结果往往较差,剪枝的效果也不好;所以我们尝试使用迭代加深DFS,每次固定警卫数(从小开始增加),初始是(m×n+4)/5,然后用DFS判断是否合法,找到合法的情况就返回。这样就能得到最少的警卫。
剪枝策略
- 按照先行再列的顺序遍历图,避免重复搜索等价状态
- 防止警卫后,出现某个陈列室的覆盖次数大于1,则直接返回(该种情况已经不符合要求)
- 最优性剪枝:普通回溯法为若当前已放置的警卫数≥已知的最少警卫数,直接回溯;但是我们采用迭代加深DFS,直接找到第一个合法的情况就是最小值,可以直接返回。
- 剩余未覆盖的格子数>剩余警卫能覆盖的最大数量(警卫数×5)也直接返回(这种情况就无法满足每个陈列室被覆盖,也不符合题目要求)
算法流程
- 初始化最小值:min_k = (m×n+4)/5,最大值:max_k = m×n
- 迭代加深DFS:遍历min_k和max_k数量的警卫
- 对每个k数量的警卫,遍历每个位置是否防止警卫,并且通过上面的剪枝策略进行剪枝
- 如果遍历完所有k依然没有结果,返回“No Solution!”
算法实现
- 数据结构:

grid是记录m×n的二维数组,记录每个格子的覆盖次数
best_plan记录最优方案的安排警卫位置
min_guards记录最小警卫数
- 核心函数
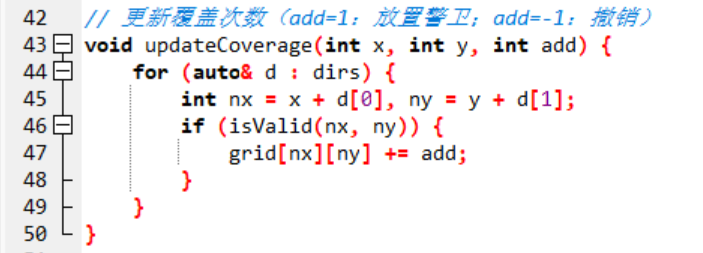
负责更新覆盖次数(放置警卫处和上下左右的合法位置的覆盖次数都加1)

判断覆盖是否合法,不能覆盖超过1次,即不能重复覆盖
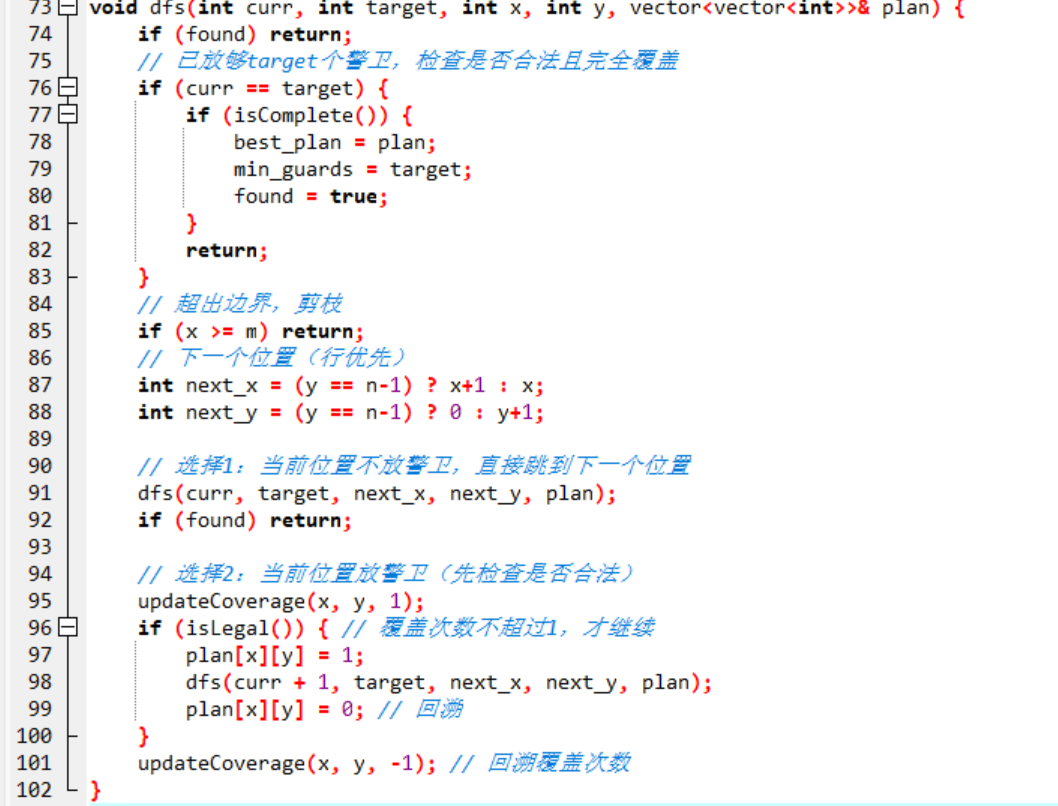
dfs深度优先搜索,每次都遍历当前位置不放警卫或者当前位置放警卫两种情况

迭代加深,初始化并且在完成计算后输出结果
性能分析
时间复杂度:
首先我们在迭代加深的函数中,需要遍历k从min_k到max_k,一共k_max-k_min+1种情况
在DFS的时候,实际上是每次从N个位置(N=m×n)选k个位置作为警卫的点,并且对于放置警卫需要更新覆盖次数,且调用isLegal检查每个格子的覆盖次数,故需要乘上N,但是由于我们的剪枝策略,这个值需要乘上一个系数α,DFS的时间复杂度是
![]()
总的时间复杂度是
![]()
其中k在min_k到max_k之间;
N=m×n;
min_k = (m×n+4)/5,max_k = m×n;
大约情况下是:
尝试将![]() 通过斯特林公式展开:
通过斯特林公式展开:![]()
则如果忽略系数则
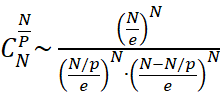
化简后忽略系数大约是
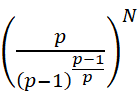
故总的时间复杂度大约是
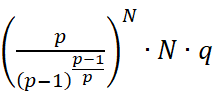
(q是系数,p是小于N大约为5的一个数)
可以发现这是一个底数大于1的指数乘上一个一次式的复杂度,比较高,但是比原先我们分析的底数为2的情况好很多
空间复杂度:
主要是两个二维数组,故空间复杂度是O(m×n)
测试
运行时间几乎是指数级上升(到15几乎就跑不出来了)
有优化空间吗?
可以考虑分治的思想,将大的矩形分为小的矩形(不过在拼接处边界处理可能存在难点)
也可以考虑用GPU优化(不过这个跟算法就没关系了)
由于DFS的特性,每次遍历到底,在探索顺序上也存在可优化点,比如优先考虑能覆盖更多位置的地方??

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容





所有评论(0)