MATLAB仿真Gough-Stewart并联机器人斯图尔特6自由度并联机器人逆运动学仿真 动力学控制pid控制 1.搭建了六自由度Stewart并联机器人simulink/simscape仿真模型 2.建立了逆向运动学仿真 输入位置和姿态求解各个杆长 3.运用pid控制器进行动力学跟踪控制 使用MATLAB进行了Gough-Stewart并联机器人的仿真。首先，我搭建了一个六自由度的Stewart并联机器人的Simulink/Simscape仿真模型。然后，我建立了逆向运动学仿真，通过输入位置和姿态来求解各个杆长。最后，我使用PID控制器进行动力学跟踪控制。 这段话涉及到的知识点和领域范围包括： MATLAB仿真：MATLAB是一种高级技术计算软件，用于数值计算、数据可视化和编程。它在工程、科学和其他领域中广泛应用。 Gough-Stewart并联机器人：Gough-Stewart并联机器人是一种具有六个自由度的机器人系统，由固定底座和可移动平台以及连接它们的杆件组成。它具有高精度和高刚度，广泛应用于精密定位和运动控制领域。 逆向运动学：逆向运动学是指根据机器人的末端位置和姿态，求解机器人各个关节的位置和角度。它是机器人控制中的重要问题，用于实现期望的末端运动。 PID控制器：PID控制器是一种常用的反馈控制器，用于调节系统的输出以使其接近期望值。它通过比较实际输出和期望输出之间的差异，并根据比例、积分和微分三个控制参数来调整控制信号，实现系统的稳定和精确控制。 延申科普： Gough-Stewart并联机器人是一种特殊的机器人系统，由固定底座和可移动平台以及连接它们的杆件组成。它的六个自由度使得它能够实现复杂的运动和定位任务。逆向运动学是解决机器人控制问题的关键之一，它通过数学模型和几何计算来求解机器人关节的位置和角度。PID控制器是一种经典的控制算法，广泛应用于工业自动化和机器人控制领域。它的优点是简单易实现，但在某些情况下可能需要调整参数以获得更好的控制效果。

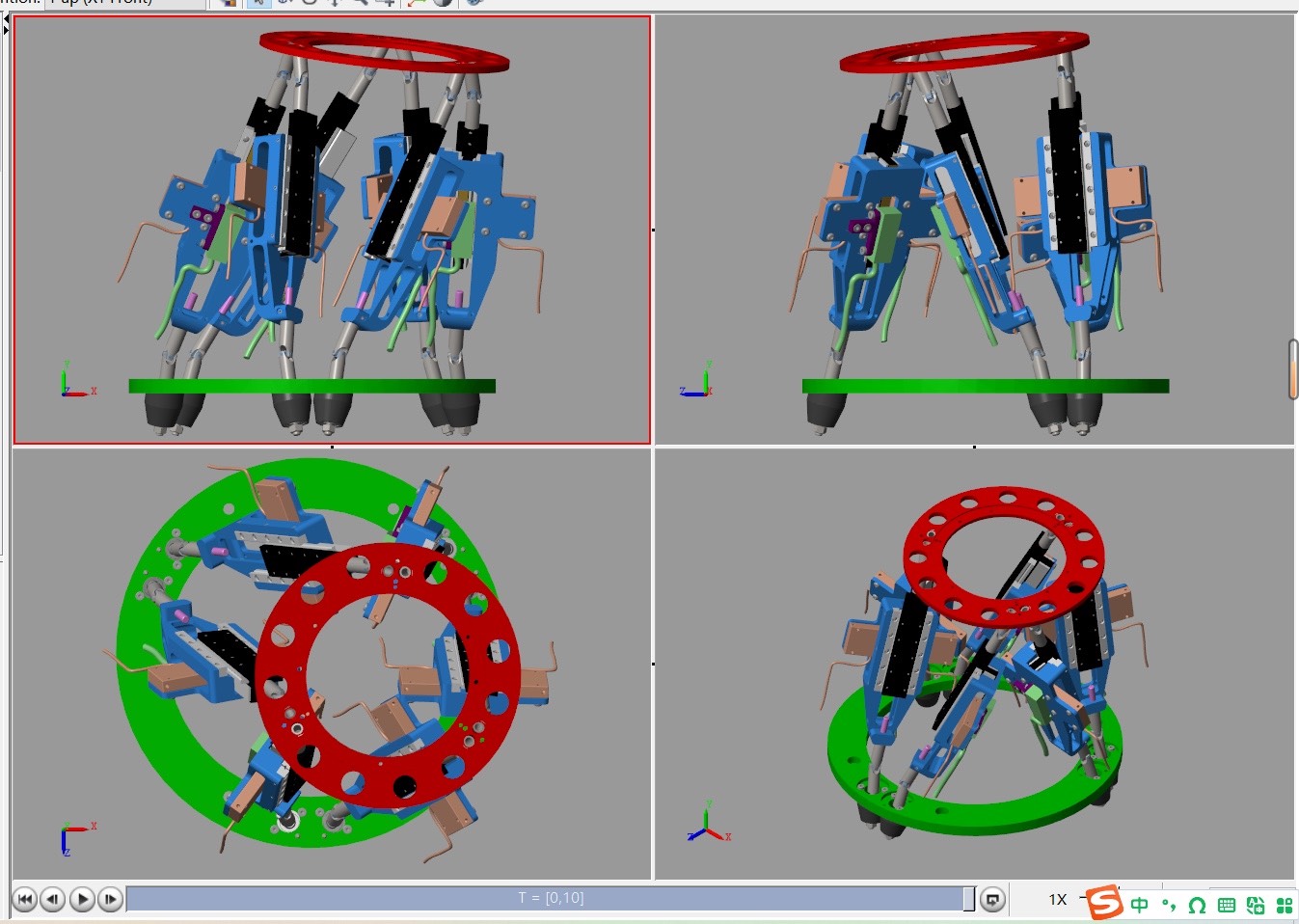
在机器人研究领域，Gough - Stewart并联机器人凭借其六个自由度，展现出在精密定位与运动控制的卓越潜力。今天，咱们就借助MATLAB，深入探索它的仿真世界。

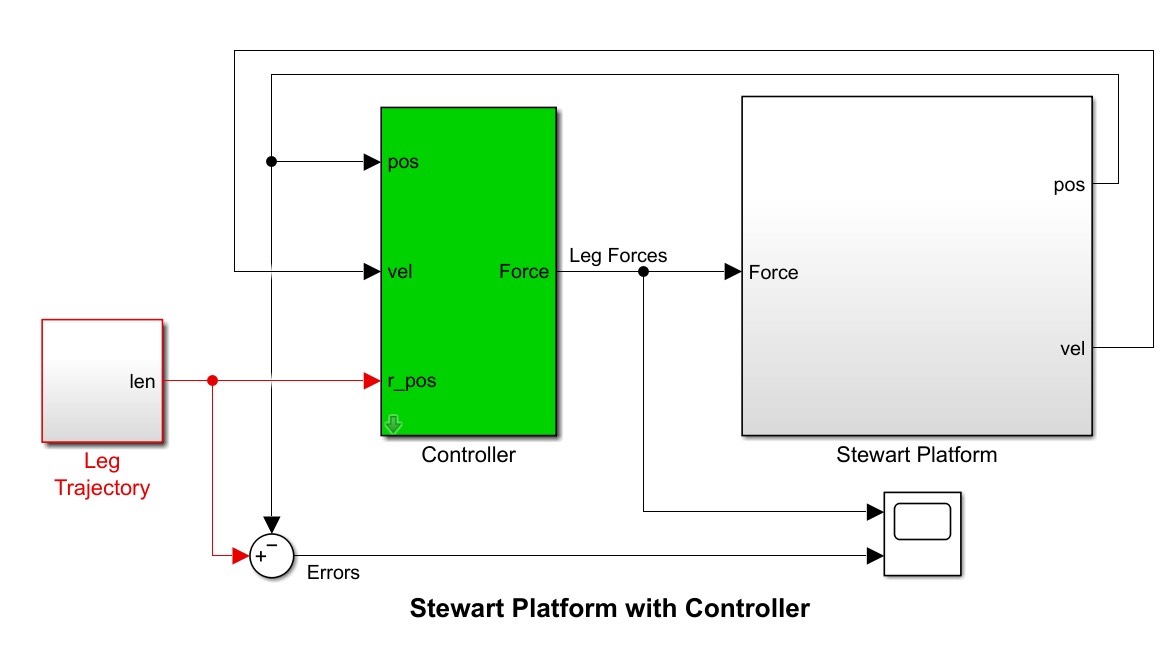
搭建Simulink/Simscape仿真模型

MATLAB的Simulink和Simscape为我们提供了便捷的建模环境。在Simulink中，我们像搭建乐高积木一样，将各个模块组合起来构建六自由度Stewart并联机器人模型。比如，我们需要定义固定底座、可移动平台以及连接它们的杆件的物理特性。

% 这里虽然没有具体代码构建Simulink模型，但可以想象类似如下定义参数
base_params = struct('mass', 10, 'inertia', [1 0 0; 0 1 0; 0 0 1]);
platform_params = struct('mass', 5, 'inertia', [0.5 0 0; 0 0.5 0; 0 0 0.5]);
link_lengths = [1 1 1 1 1 1];

这里简单定义了底座和平台的质量、惯性以及杆件长度，实际建模中这些参数需更精确地测量与计算，然后通过Simscape的机械元件模块来搭建真实物理特性的模型。

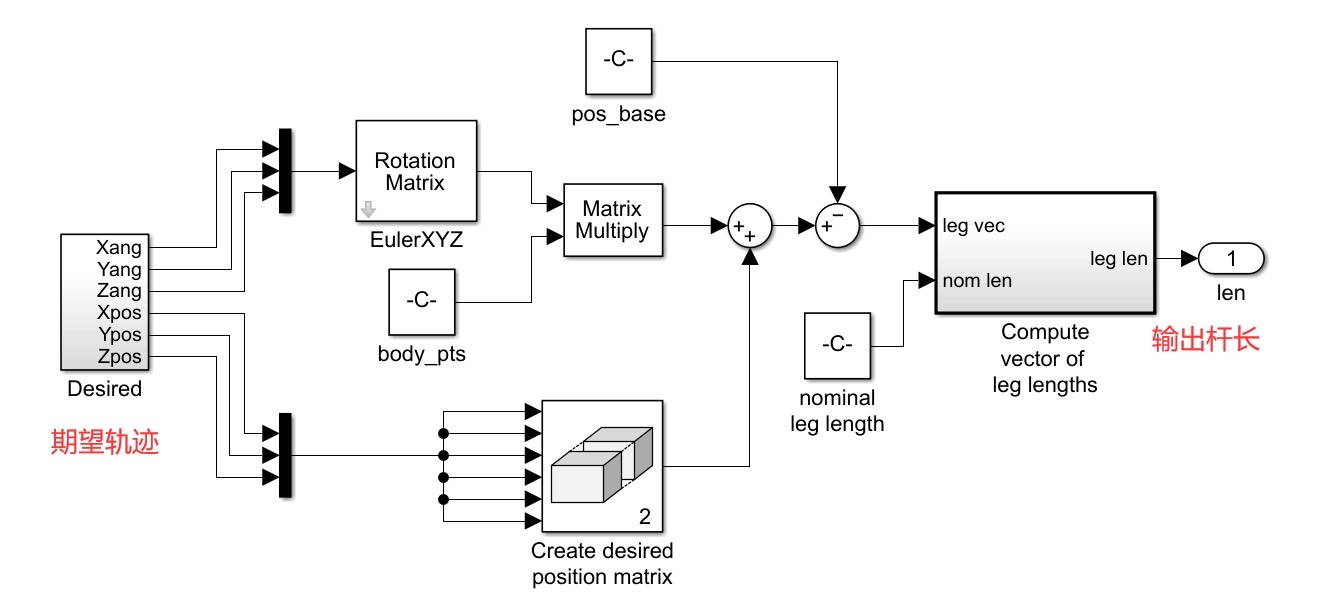
逆向运动学仿真

逆向运动学对于机器人控制至关重要。我们的目标是根据给定的末端位置和姿态，求解各个杆长。这就好比知道了机器人最终要到达的地方，反推每个关节需要怎么动。

假设我们已知平台在空间中的位置 [x, y, z] 和姿态（用欧拉角 [phi, theta, psi] 表示），我们可以通过如下简单代码示例（实际需更复杂的几何与数学推导）来近似求解杆长。

% 简单示例，非完整精确代码
function lengths = inverse_kinematics(x, y, z, phi, theta, psi)
    % 这里省略复杂的几何变换与计算
    % 简单假设一种线性关系
    lengths = [x + y + z + phi + theta + psi; x - y + z - phi + theta - psi;
               -x + y + z + phi - theta + psi; -x - y + z - phi - theta + psi;
               x + y - z + phi + theta - psi; x - y - z + phi - theta - psi];
end

上述代码只是为了展示概念，实际逆向运动学计算要基于机器人的几何结构，利用向量运算、旋转矩阵等数学工具，精确计算出每个杆件的长度。

PID控制器实现动力学跟踪控制

PID控制器是工业自动化和机器人控制的常客。它通过不断调整比例（P）、积分（I）、微分（D）参数，让系统输出尽可能接近期望值。

% PID控制器简单代码示例
Kp = 1;
Ki = 0.1;
Kd = 0.01;
error_sum = 0;
prev_error = 0;
setpoint = 10; % 期望输出值
current_output = 5; % 当前实际输出值

for i = 1:100
    error = setpoint - current_output;
    error_sum = error_sum + error;
    derivative = error - prev_error;
    control_signal = Kp * error + Ki * error_sum + Kd * derivative;
    % 根据控制信号调整系统输入，这里省略具体调整代码
    current_output = current_output + control_signal; % 简单模拟输出变化
    prev_error = error;
end

在机器人动力学控制中，我们将期望的运动轨迹作为设定值，机器人实际运动状态作为反馈值，通过PID控制器不断调整控制信号，让机器人尽可能精确地跟踪期望轨迹。

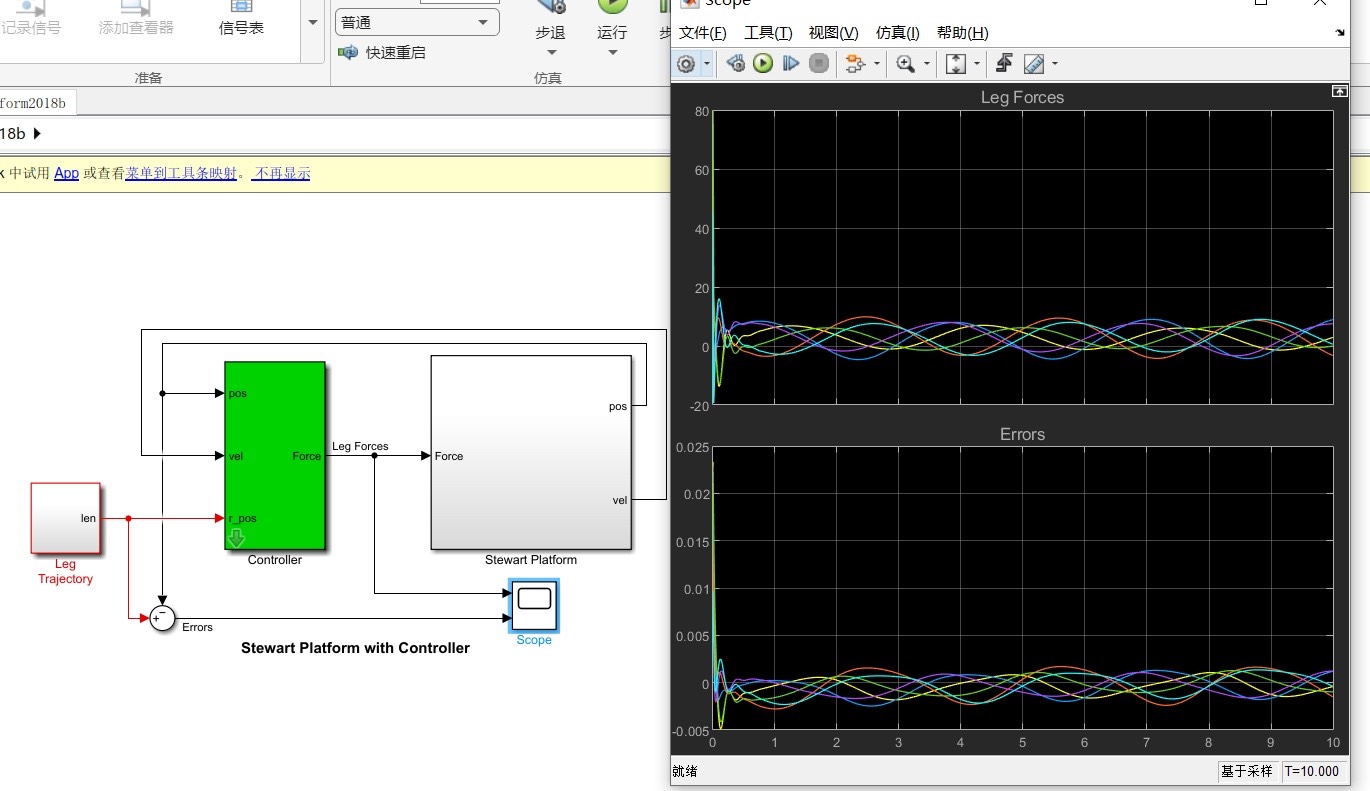
通过MATLAB搭建模型、求解逆运动学以及运用PID控制，我们能深入理解Gough - Stewart并联机器人的工作原理与控制方法，为实际应用打下坚实基础。