六自由度机械臂建模仿真（matlab程序），有控制面板，代码可流畅运行 1、机器人运动学正逆解、动力学建模仿真与轨迹规划，雅克比矩阵求解 2、蒙特卡洛采样画出末端执行器工作空间 3、基于时间最优的改进粒子群优化算法机械臂轨迹规划设计

在机器人领域，六自由度机械臂因其高度的灵活性和广泛的应用场景，一直是研究的热门对象。今天咱就聊聊如何通过Matlab来实现六自由度机械臂的建模仿真，还带着个控制面板，代码跑起来溜溜的。

一、机器人运动学正逆解、动力学建模仿真与轨迹规划，雅克比矩阵求解

运动学正解

运动学正解就是已知机械臂各个关节的角度，求末端执行器的位置和姿态。在Matlab里，咱们可以借助Robotics System Toolbox来简化这个过程。假设我们已经定义好了机械臂的DH参数（Denavit - Hartenberg参数），代码示例如下：

% 定义DH参数
L1 = Link('d', 0.1, 'a', 0, 'alpha', pi/2);
L2 = Link('d', 0, 'a', 0.2, 'alpha', 0);
L3 = Link('d', 0, 'a', 0.2, 'alpha', 0);
L4 = Link('d', 0.3, 'a', 0, 'alpha', pi/2);
L5 = Link('d', 0, 'a', 0, 'alpha', -pi/2);
L6 = Link('d', 0.1, 'a', 0, 'alpha', 0);

robot = SerialLink([L1 L2 L3 L4 L5 L6], 'name', 'MyRobot');
% 设定关节角度
q = [pi/4, pi/6, pi/8, pi/10, pi/12, pi/14];
% 求解运动学正解
T = robot.fkine(q);

这里，通过Link函数定义每个关节的DH参数，再用SerialLink组合成完整的机械臂模型。fkine函数就是用来求解运动学正解的，输入关节角度q，就能得到末端执行器的齐次变换矩阵T。

运动学逆解

运动学逆解和正解相反，是已知末端执行器的位置和姿态，求各个关节的角度。Matlab里直接用ikine函数就能搞定：

% 假设已知目标位置和姿态
T_target = transl(0.5, 0.3, 0.4) * trotz(pi/3) * troty(pi/4) * trotx(pi/5);
% 求解运动学逆解
q_sol = robot.ikine(T_target);

transl和trotx、troty、trotz等函数用来构建目标的齐次变换矩阵Ttarget，ikine函数求解出满足该目标的关节角度qsol。

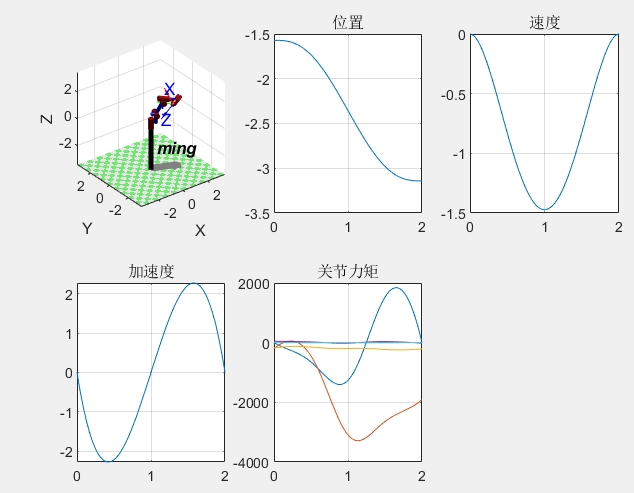
动力学建模仿真

动力学建模主要是研究机械臂运动时的力和力矩关系。在Matlab里，我们可以利用robot.dyn函数来获取机械臂的动力学参数。

% 获取动力学参数
M = robot.dyn(q, 'M'); % 惯性矩阵
C = robot.dyn(q, 'C'); % 科里奥利力和离心力矩阵
G = robot.dyn(q, 'G'); % 重力向量

通过这些参数，我们就能进一步做动力学仿真，比如模拟在特定外力作用下机械臂的运动。

轨迹规划

轨迹规划就是让机械臂按照我们期望的路径运动。常见的有笛卡尔空间轨迹规划和关节空间轨迹规划。下面是一个简单的关节空间轨迹规划示例：

% 起始和目标关节角度
q_start = [0, 0, 0, 0, 0, 0];
q_end = [pi/2, pi/3, pi/4, pi/5, pi/6, pi/7];
% 规划轨迹
t = 0:0.01:5; % 时间向量
q_path = jtraj(q_start, q_end, t);

jtraj函数根据起始和目标关节角度，在给定的时间向量t内规划出一条平滑的关节空间轨迹q_path。

雅克比矩阵求解

雅克比矩阵描述了关节速度和末端执行器速度之间的关系。在Matlab里用jacob0函数就能得到：

J = robot.jacob0(q);

这个J矩阵对于很多控制算法都非常重要，比如在速度控制中，我们可以通过它来计算需要给各个关节施加的速度。

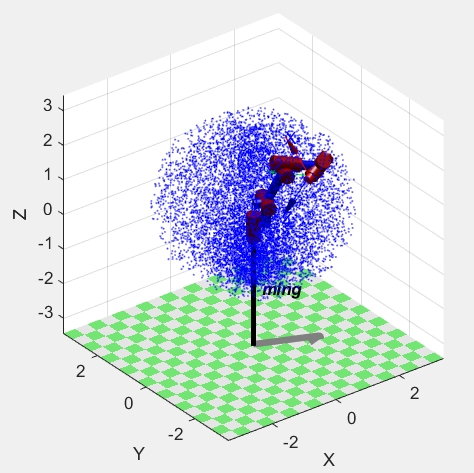
二、蒙特卡洛采样画出末端执行器工作空间

蒙特卡洛采样是一种通过随机采样来估计工作空间的方法。代码如下：

num_samples = 10000;
workspace = zeros(num_samples, 3);
for i = 1:num_samples
    % 随机生成关节角度
    q_random = 2 * pi * rand(6, 1);
    T = robot.fkine(q_random);
    workspace(i, :) = T(1:3, 4);
end
scatter3(workspace(:, 1), workspace(:, 2), workspace(:, 3));
xlabel('X');
ylabel('Y');
zlabel('Z');
title('End - Effector Workspace');

这里我们随机生成num_samples组关节角度，通过运动学正解得到对应的末端执行器位置，然后用scatter3函数将这些位置点画出来，就能直观看到末端执行器的工作空间啦。

三、基于时间最优的改进粒子群优化算法机械臂轨迹规划设计

粒子群优化算法（PSO）是一种智能优化算法。改进的PSO算法可以用来寻找时间最优的轨迹。下面是一个简化的实现思路：

% 初始化粒子群
num_particles = 50;
num_dimensions = length(q_path);
particles = rand(num_particles, num_dimensions);
velocities = zeros(num_particles, num_dimensions);
% 定义适应度函数（这里简化为时间相关的函数）
fitness = @(x) sum(diff(x).^2);
% 迭代更新粒子位置和速度
for iter = 1:100
    for i = 1:num_particles
        fitness_values(i) = fitness(particles(i, :));
        if fitness_values(i) < fitness(pbest_fitness(i))
            pbest(i, :) = particles(i, :);
            pbest_fitness(i) = fitness_values(i);
        end
    end
    [global_best_fitness, global_best_index] = min(pbest_fitness);
    global_best = pbest(global_best_index, :);
    % 更新速度和位置
    w = 0.7; % 惯性权重
    c1 = 1.5; % 学习因子1
    c2 = 1.5; % 学习因子2
    r1 = rand(num_particles, num_dimensions);
    r2 = rand(num_particles, num_dimensions);
    velocities = w * velocities + c1 * r1.* (pbest - particles) + c2 * r2.* (repmat(global_best, num_particles, 1) - particles);
    particles = particles + velocities;
end

这里我们初始化了粒子群，定义了一个简单的适应度函数（和运动时间相关），然后通过不断迭代更新粒子的位置和速度，最终找到一个近似的时间最优轨迹。

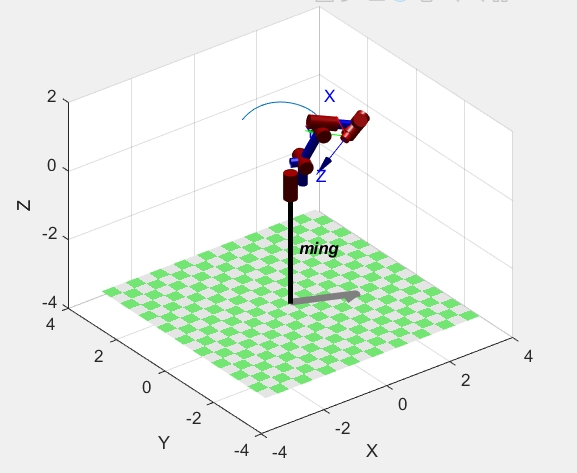
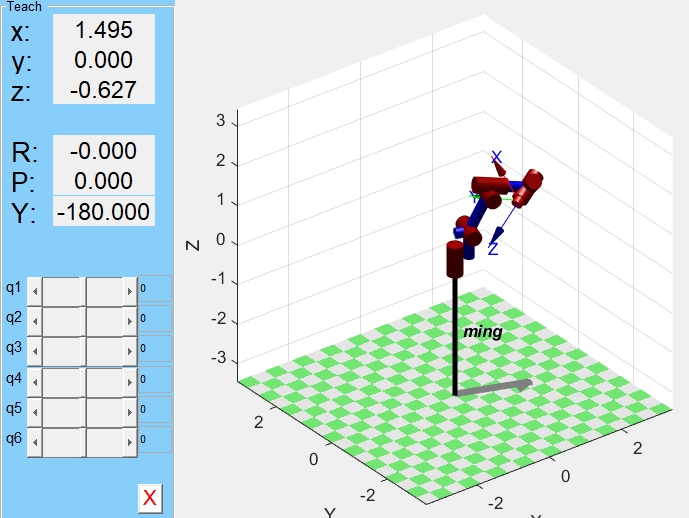
有了这些内容，再搭配上一个控制面板，就能更方便地对六自由度机械臂进行各种操作和观察啦。无论是调整参数，还是切换不同的仿真模式，都能让整个建模仿真过程更加直观和有趣。希望大家也能通过Matlab深入探索六自由度机械臂的奇妙世界。