一起探索机器学习

Machine learning

Logistic

CSDN：

https://blog.csdn.net/weixin_45814668知乎：

https://www.zhihu.com/people/qiongjian0427Git：

https://github.com/qiongjian/Machine-learning/

运行环境：anaconda—jupyter notebook

Python版本：Python3

 

数据集

下图所示为数据集。

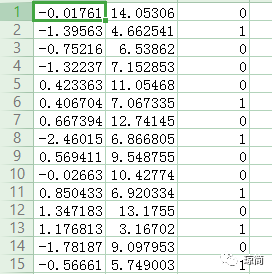
公众号回复本文题目下载

 

训练算法：找到最佳参数

‍

数据集有100个样本点，每个点包含两个数值型特征：X1和X2。

在此数据集上，我们将通过使用梯度上升法找到最佳回归系数，也就是拟合出Logistic回归模型的最佳参数。

梯度上升法的伪代码如下：

每个回归系数初始化为1重复R次：    计算整个数据集的梯度    使用alpha*gradient更新回归系数的向量返回回归系数

正式代码，在python中新建logRegres.ipynp的文件，输入下面代码：

from numpy import *def loadDataSet():#函数功能为打开文本文件并逐行读取    dataMat = [];labelMat = []    fr = open('TestSet.txt')    for line in fr.readlines():        lineArr = line.strip().split()        # 为了方便计算，我们将 X0 的值设为 1.0 ，也就是在每一行的开头添加一个 1.0 作为 X0        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])        labelMat.append(int(lineArr[2]))    return dataMat, labelMatdef sigmoid(inX):    return 1.0/(1+exp(-inX))#输入数据特征与数据的类别标签def gradAscent(dataMatIn, classLabels):    #转换为numpy型    dataMatrix = mat(dataMatIn)     # transpose() 行列转置函数    labelMat = mat(classLabels).transpose()    m,n = shape(dataMatrix)    alpha = 0.001 #步长    maxCycles = 500 #迭代次数       #初始化权值向量，每个维度均为1.0    weights = ones((n,1))    for k in range(maxCycles):        h = sigmoid(dataMatrix * weights)        error = (labelMat - h)        weights = weights + alpha * dataMatrix.transpose() * error    return weights

看看结果：

已经求出回归系数[w0,w1,w2]。

 

分析数据：画出决策边界

上面已经解出一组回归系数，它确定了不同类别数据之间的分隔线。那么怎样画出该分隔线，从而使得优化的过程便于理解呢？

画出数据集

def plotBestFit(weights):    import matplotlib.pyplot as plt    dataMat, labelMat = loadDataSet()    dataArr = array(dataMat)    # n->数据量，样本数    n = shape(dataArr)[0]    #xcord1,ycord1代表正例特征    #xcord2,ycord2代表负例特征    xcord1 = []; ycord1 = []    xcord2 = []; ycord2 = []    #循环筛选出正负集    for i in range(n):        if int(labelMat[i]) == 1:            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i, 2])        else:            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i, 2])    fig = plt.figure()    ax = fig.add_subplot(111)    ax.scatter(xcord1, ycord1, s = 30, c = 'red', marker = 's')    ax.scatter(xcord2, ycord2, s = 30, c = 'green')    plt.xlabel('X1')    plt.ylabel('X2')    plt.title('DataSet')    plt.show()

‍

运行结果：

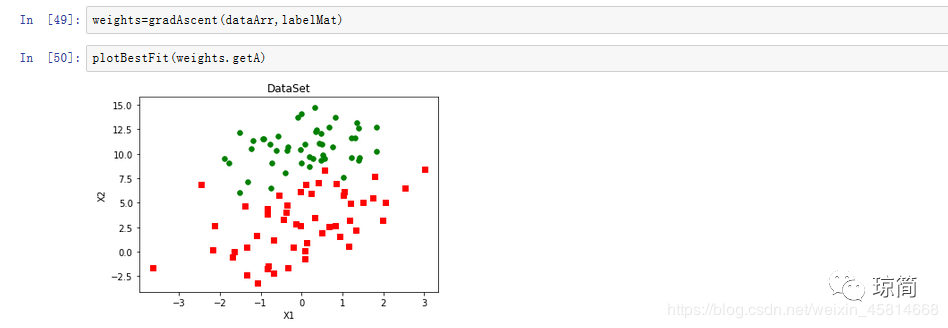
画出最佳拟合曲线

import mathfrom numpy import *def plotBestFit(weights):    import matplotlib.pyplot as plt    dataMat,labelMat=loadDataSet()    dataArr=array(dataMat)    n=shape(dataArr)[0]    #xcord1,ycord1代表正例特征    #xcord2,ycord2代表负例特征    xcord1=[];ycord1=[]    xcord2=[];ycord2=[]#循环筛选出正负集    for i in range(n):        if int(labelMat[i])==1:            xcord1.append(dataArr[i,1]);ycord1.append(dataArr[i,2])        else:            xcord2.append(dataArr[i,1]);ycord2.append(dataArr[i,2])    fig=plt.figure()    ax=fig.add_subplot(111)    ax.scatter(xcord1,ycord1,s=30,c='red',marker='s')    ax.scatter(xcord2,ycord2,s=30,c='green')#设定边界直线x和y的值    x=arange(-3.0,3.0,0.1)    y=(-weights[0]-weights[1]*x)/weights[2]    ax.plot(x,y)    plt.xlabel('X1');plt.ylabel('X2');    plt.show()

‍

运行结果：

dataArr,labelMat=loadDataSet()weights=gradAscent(dataArr,labelMat)plotBestFit(weights.getA())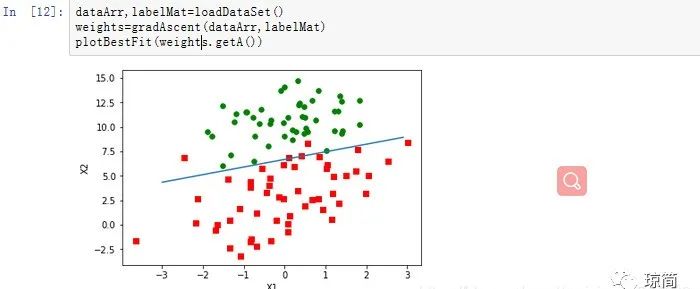

 

训练算法：随机梯度上升

梯度上升法每次更新回归系数都需要遍历整个数据集，当样本数量100个时，该方法尚可，但是当样本数据集非常大且特征非常多时，那么随机梯度下降法的计算复杂度就会特别高。
一种改进的方法是一次仅用一个样本点来更新回归系数，即随机梯度上升法。由于可以在新样本到来时对分类器进行增量式更新，因此随机梯度上升法是一个在线学习算法。
随机梯度上升法可以写成如下伪代码：

所有回归系数初始化为1对数据集中每个样本        计算该样本的梯度　　    使用alpha*gradient更新回顾系数值 返回回归系数值

‍

以下是实现代码：

def stoGradAscent0(dataMatrix, classLabels):    m, n = shape(dataMatrix)    alpha = 0.01    weights = ones(n)    for i in range(m):        h = sigmoid(sum(dataMatrix[i] * weights))        error = classLabels[i] - h        weights = weights + alpha * error * dataMatrix[i]    return weights

‍

随机梯度上升和梯度上升法在代码上的区别：
1.后者的变量h和误差error都是向量。
2.前者没有矩阵的转换过程，所有变量的数据类型都是Numpy数组。

代码运行结果：

dataArr,labelMat = loadDataSet()weights=stoGradAscent0(array(dataArr),labelMat)plotBestFit(weights)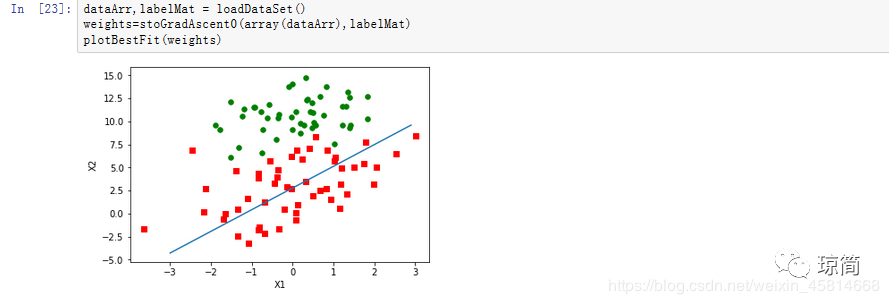

拟合曲线错了三分之一的样本，要进行改进。

改进的下次再说。

—— E N D ——

闹钟一响就起

走了就不回头

开开心心

ID:qiongjian0427

关注我，一起学习机器学习~