【计算器】四则运算的算法实现
四则运算的算法实现
先实现整数部分
加减乘比较简单, 可以参考: 高精度算法全套(加,减,乘,除,全网最详细). 除法我参考的是: 大数加减乘除运算总结
四则运算相关的OJ题目
关于除法
基本上参考的是: 大数加减乘除运算总结
最简单的办法就是使用减法, 但是这样就会导致效率极其低下, 所以我们应该把这个过程加速
一个可用的代码
- 这份代码包含了整数的四则运算
- 可以用这个题目进行验证: https://tioj.ck.tp.edu.tw/problems/1006
- 运行效率如下
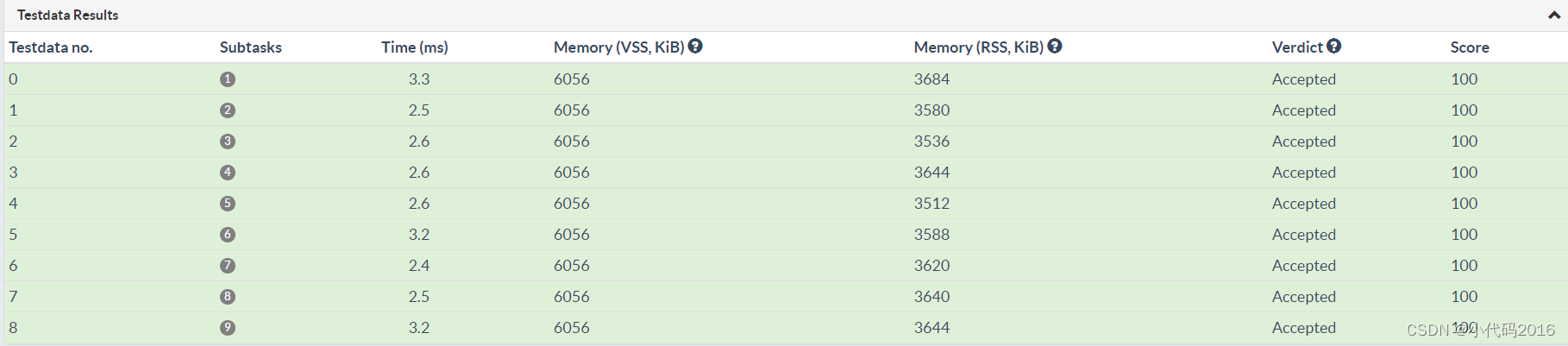
#include <iostream>
#include <string>
#include <memory>
#include <algorithm>
int compare(std::string x, std::string y) {
if (x.size() < y.size()) {
return -1;
}
if (x.size() > y.size()) {
return 1;
}
return x.compare(y);
}
std::string add(std::string x, std::string y) {
/**
* 对齐数字
* x = 123 , y = 4567
* x = 0123 , y = 4567
*/
if (x.size() != y.size()) {
if (x.size() > y.size()) {
int len = x.size() - y.size();
for (int i = 0; i < len; i++) {
y.insert(0, "0");
}
} else {
int len = y.size() - x.size();
for (int i = 0; i < len; i++) {
x.insert(0, "0");
}
}
}
/**
* 对齐后的字符串转换为倒置的 int 数组
* x = 0123 , y = 4567
* x = 3210 , y = 7654
*/
char *sx = const_cast<char *>(x.c_str());
char *sy = const_cast<char *>(y.c_str());
const int len = x.size();
auto a = std::make_unique<int[]>(len);
auto b = std::make_unique<int[]>(len);
for (int i = 0; i < len; i++) {
a[len - 1 - i] = sx[i] - '0';
}
for (int i = 0; i < len; i++) {
b[len - 1 - i] = sy[i] - '0';
}
/** 计算 */
const int size = len + 1;
auto c = std::make_unique<int[]>(size);
for (int i = 0; i < len; i++) {
c[i] += a[i] + b[i];
// 处理进位
if (c[i] >= 10) {
c[i + 1] += c[i] / 10;
c[i] = c[i] % 10;
}
}
/** 翻转计算结果 */
std::string str;
int i = size - 1;
// 删除前导0
if (0 == c[i]) {
i--;
}
// 拼接计算结果
while (i >= 0) {
str.push_back(c[i] + '0');
i--;
}
return str;
}
std::string substract(std::string x, std::string y) {
// 结果是否为负数
bool isNegativeNumber = false;
/**
* 对齐数字
* x = 123 , y = 4567
* x = 0123 , y = 4567
*/
if (x.size() != y.size()) {
if (x.size() > y.size()) {
int len = x.size() - y.size();
for (int i = 0; i < len; i++) {
y.insert(0, "0");
}
} else {
int len = y.size() - x.size();
for (int i = 0; i < len; i++) {
x.insert(0, "0");
}
}
}
/**
* 数字排序
* s1 为较大数字
* s2 为较小数字
*/
std::string s1 = x;
std::string s2 = y;
if (s1.compare(s2) < 0) {
s1 = y;
s2 = x;
isNegativeNumber = true;
}
/**
* 对齐后的字符串转换为倒置的 int 数组
* x = 0123 , y = 4567
* x = 3210 , y = 7654
*/
char *sx = const_cast<char *>(s1.c_str());
char *sy = const_cast<char *>(s2.c_str());
const int len = s1.size();
auto a = std::make_unique<int[]>(len);
auto b = std::make_unique<int[]>(len);
for (int i = 0; i < len; i++) {
a[len - 1 - i] = sx[i] - '0';
}
for (int i = 0; i < len; i++) {
b[len - 1 - i] = sy[i] - '0';
}
/** 计算 */
const int size = len;
auto c = std::make_unique<int[]>(size);
for (int i = 0; i < len; i++) {
// 借位处理
if (a[i] < b[i]) {
a[i + 1]--;
a[i] += 10;
}
c[i] = a[i] - b[i];
}
/** 翻转计算结果 */
std::string str;
int i = size - 1;
// 删除前导0
while (0 == c[i] && i >= 1) {
i--;
}
// 添加负号
if (isNegativeNumber) {
str.push_back('-');
}
// 拼接计算结果
while (i >= 0) {
str.push_back(c[i] + '0');
i--;
}
return str;
}
std::string multiply(std::string x, std::string y) {
/**
* 字符串转换为倒置的 int 数组
* x = 123 , y = 4567
* x = 321 , y = 7654
*/
char *sx = const_cast<char *>(x.c_str());
char *sy = const_cast<char *>(y.c_str());
const int la = x.size() + 1;
const int lb = y.size() + 1;
auto a = std::make_unique<int[]>(la);
auto b = std::make_unique<int[]>(lb);
for (int i = 1; i < la; i++) {
a[la - i] = sx[i - 1] - '0';
}
for (int i = 1; i < lb; i++) {
b[lb - i] = sy[i - 1] - '0';
}
/** 计算 */
const int lc = x.size() + y.size() + 1;
auto c = std::make_unique<int[]>(lc);
for (int i = 1; i < la; i++) {
for (int j = 1; j < lb; j++) {
c[i + j - 1] += a[i] * b[j];
c[i + j] += c[i + j - 1] / 10;
c[i + j - 1] %= 10;
}
}
/** 翻转计算结果 */
std::string str;
int i = lc - 1;
while (0 == c[i] && i > 1) {
i--;
}
// 拼接计算结果
while (i >= 1) {
str.push_back(c[i] + '0');
i--;
}
return str;
}
std::string divide(std::string x, std::string y) {
// 被除数为 0 或者被除数小于除数, 均返回 0
if (0 == x.compare("0") || compare(x, y) < 0) {
return "0";
}
// 相等直接返回 1
if (0 == compare(x, y)) {
return "1";
}
// 除数为 1 , 直接返回被除数
if (0 == y.compare("1")) {
return x;
}
std::string str = "0";
std::string remainder;
// 被除数只比除数多一位, 则使用减法
if (x.size() - y.size() < 2) {
// 余数
remainder = x;
while (compare(remainder, y) >= 0) {
remainder = substract(remainder, y);
str = add(str, "1");
}
} else {
// 被除数比除数多两位或以上, 先用加法再用减法
// 余数
str = "0";
std::string times = "1";
std::string num = y;
std::string t = x;
while (t.size() - y.size() >= 2) {
while (compare(num, t) <= 0) {
remainder = num;
num = add(num, num);
if (compare(num, t) > 0) {
num = y;
str = add(str, times);
times = "1";
t = substract(t, remainder);
break;
}
times = multiply(times, "2");
}
}
remainder = t;
if (compare(remainder, y) >= 0) {
while (compare(remainder, y) >= 0) {
remainder = substract(remainder, y);
str = add(str, "1");
}
}
}
// std::cout << str << std::endl;
// std::cout << remainder << std::endl;
return str;
}
int main() {
std::string s1, s2;
std::cin >> s1;
std::cin >> s2;
std::cout << divide(s1, s2) << std::endl;
return 0;
}
算法实现解释
按照 大数加减乘除运算总结 所讲解得思路, 我们可以用扩大除数或者二分倍数的方法. 扩大除数的方法没想出来怎么实现, 二分倍数的倒是想出来了.我们以 11111/9为例进行讲解.
使用python命令行计算结果
Python 3.10.9 (tags/v3.10.9:1dd9be6, Dec 6 2022, 20:01:21) [MSC v.1934 64 bit (AMD64)] on win32
Type "help", "copyright", "credits" or "license" for more information.
>>> 11111/9
1234.5555555555557
>>>
思路如下:
- 如果被除数的长度-除数的长度 >= 2, 那么使用加法模拟, 计算过程就是除数不停的乘以2, 商也就是不停的乘以2, 直到加法计算结果大于等于被除数
- 如果上一步的余数的长度 - 除数长度 >= 2, 重复步骤 1, 否则进入步骤3
- 如果余数长度 - 除数长度 >= 0 进入步骤4 , 否则进入步骤5
- 使用减法进行计算
- 累加每一轮的商
现在我们新建一个文本文档, 复制如下代码并观察
# 被除数 除数 商 余数
11111 / 9 = 1234 ... 5
9+9=18 # 第 1 次累加
1*2=2 # 此时商为 2
18+18=36 # 第 2 次累加
2*2=4 # 此时商为 4
36+36=72 # 第 3 次累加
4*2=8 # 此时商为 8
72+72=144
8*2=16
144+144=288
16*2=32
288+288=576
32*2=64
576+576=1152
64*2=128
1152+1152=2304
128*2=256
2304+2304=4608
256*2=512
4608+4608=9216 # 第 10 次累加
512*2=1024 # 此时商为 1024
9216+9216=18432 # 此时累加已经超过了被除数 11111 , 这一轮计算结束
如果此时结束计算, 那么商为1024, 余数为 11111-9216=1895.
然后我们计算第二轮:1895/9
9+9=18 # 第 1 次累加
1*2=2 # 此时商为 2
18+18=36 # 第 2 次累加
2*2=4 # 此时商为 4
36+36=72 # 第 3 次累加
4*2=8 # 此时商为 8
72+72=144
8*2=16
144+144=288
16*2=32
288+288=576
32*2=64
576+576=1152
64*2=128
1152+1152=2304 # 此时商为 128
如果此时结束计算, 那么商为128, 余数为 1895-1152=743.
然后我们计算第三轮:743/9
9+9=18 # 第 1 次累加
1*2=2 # 此时商为 2
18+18=36 # 第 2 次累加
2*2=4 # 此时商为 4
36+36=72 # 第 3 次累加
4*2=8 # 此时商为 8
72+72=144
8*2=16
144+144=288
16*2=32
288+288=576
32*2=64
576+576=1152 # 此时商为 64
如果此时结束计算, 那么商为64, 余数为 743-576=167.
然后我们计算第四轮:167/9
9+9=18 # 第 1 次累加
1*2=2 # 此时商为 2
18+18=36 # 第 2 次累加
2*2=4 # 此时商为 4
36+36=72 # 第 3 次累加
4*2=8 # 此时商为 8
72+72=144
8*2=16
144+144=288 # 此时商为 16
如果此时结束计算, 那么商为16, 余数为 167-144=23.
至此, 我们一共使用了 10+7+6+4=27次加法, 10+7+6+4=27次乘法. 现在我们得到的计算结果为:
商: 1024+128+64+16=1232
余数为: 23
然后我们使用减法计算
23-9=14 # 此时商为 1232+1=1233
14-9=5 # 此时余数小于除数, 计算结束, 商为 1233+1=1234, 余数为 5
最终计算结果与我们的期望一致
上面使用加法计算商的部分, 其实可以不用乘法而用加法. 这样的话, 我们共用了 27+27+2=56次加法, 而单纯的用减法, 那就要1234+1=1235次, 两种方法的运行效率不可同日而语.
模仿 java 的 BigDecimal 设计 API
现在我们可以实现真正的大数计算了, 课参考如下java代码设计API
package com.laolang.hello.decimal;
import java.math.BigDecimal;
import java.text.DecimalFormat;
import org.testng.annotations.Test;
public class BigDecimalStudyTest {
@Test
public void base_useage_test() {
// 三种初始化
BigDecimal d1 = new BigDecimal(1);
BigDecimal d2 = new BigDecimal(1L);
BigDecimal d3 = new BigDecimal("1");
// 加
d1.add(d2);
// 减
d1.subtract(d2);
// 乘
d1.multiply(d2);
// 除
// d2: 除数
// 3: 精确到小数点后几位, 默认为 0
// BigDecimal.ROUND_HALF_UP: 四舍五入
d1.divide(d2, 3, BigDecimal.ROUND_HALF_UP);
}
@Test
public void format_useage_test() {
BigDecimal d1 = new BigDecimal("12345.6789");
DecimalFormat df1 = new DecimalFormat("0.00");
System.out.println(df1.format(d1)); // 1234.18
DecimalFormat df2 = new DecimalFormat("#.00");
System.out.println(df2.format(d1)); // 1234.18
}
}
完成后的代码
目录结构
源码
基本测试过程
遇到的问题
判断一个字符串是否为合法的数字
题目: 65. 有效数字
参考资料: LeetCode:Valid Number - 判断字符串中内容是否为数字
其实没有看这篇博客, 因为我写完以后发现比他的快多了, 测试了几次最慢8ms, 最快0ms
一个可用的代码
#include <string>
#include <cctype>
class Solution {
public:
// 是否加法符号
bool isPlusSign(char ch) {
return ch == '+';
}
// 是否减法符号
bool isSubstractSign(char ch) {
return ch == '-';
}
// 是否 . 符号
bool isDotSign(char ch) {
return ch == '.';
}
// 是否 e 或 E
bool isScientificSign(char ch) {
return ch == 'e' || ch == 'E';
}
// 是否数字
bool isNumber(std::string s) {
if (s.empty()) {
return false;
}
int plusSignCount = 0;
int substractSignCount = 0;
int dotSignCount = 0;
int scientificSignCount = 0;
int digitCount = 0;
auto chars = s.c_str();
const int len = s.size();
bool flag = true;
char prev = 0;
int scientificSignIndex = 0;
// +00123.456e-789
for (int i = 0; i < len; i++) {
char ch = chars[i];
if (i >= 1) {
prev = chars[i - 1];
}
if (isdigit(ch)) {
digitCount += 1;
} else {
if (isPlusSign(ch)) {
plusSignCount += 1;
// 如果 + 存在, 那么最多存在两个
if (plusSignCount > 2) {
flag = false;
break;
}
// 如果 + 不在首位,那么前一个字符必须是 [e,E], 并且不能出现在最后以为
if (i > 0 && (!isScientificSign(prev) || i == (len - 1))) {
flag = false;
break;
}
} else if (isSubstractSign(ch)) {
substractSignCount += 1;
// 如果 - 存在, 那么最多存在两个
if (plusSignCount > 2) {
flag = false;
break;
}
// 如果 - 不在首位,那么前一个字符必须是 [e,E]
if (i > 0 && (!isScientificSign(prev) || i == (len - 1))) {
flag = false;
break;
}
} else if (isDotSign(ch)) {
// 不能只包含一个 .
if (0 == i && 1 == len) {
flag = false;
break;
}
dotSignCount += 1;
// 如果 . 存在, 则只能存在一个
if (dotSignCount > 1) {
flag = false;
break;
}
// . 不能在 [e,E] 之后
if (scientificSignCount > 0) {
flag = false;
break;
}
} else if (isScientificSign(ch)) {
// [e,E] 不能出现在首位
if (0 == i) {
flag = false;
break;
}
// [e,E] 不能出现在最后一位
if ( i == (len - 1)) {
flag = false;
break;
}
// 如果 [e,E] 在第二位, 首位必须是数字
if ( 1 == i && (isPlusSign(prev) || isSubstractSign(prev) || isDotSign(prev) || !isdigit(prev))) {
flag = false;
break;
}
scientificSignIndex = i;
scientificSignCount += 1;
// 如果 [e,E] 存在, 则只能存在一个
if (scientificSignCount > 1) {
flag = false;
break;
}
} else {
// 非法字符
flag = false;
break;
}
}
}
// 必须包含数字
if ( 0 == digitCount) {
flag = false;
}
return flag;
}
};
int main() {
Solution s;
bool flag = s.isNumber(".1");
return 0;
}
运行效率如下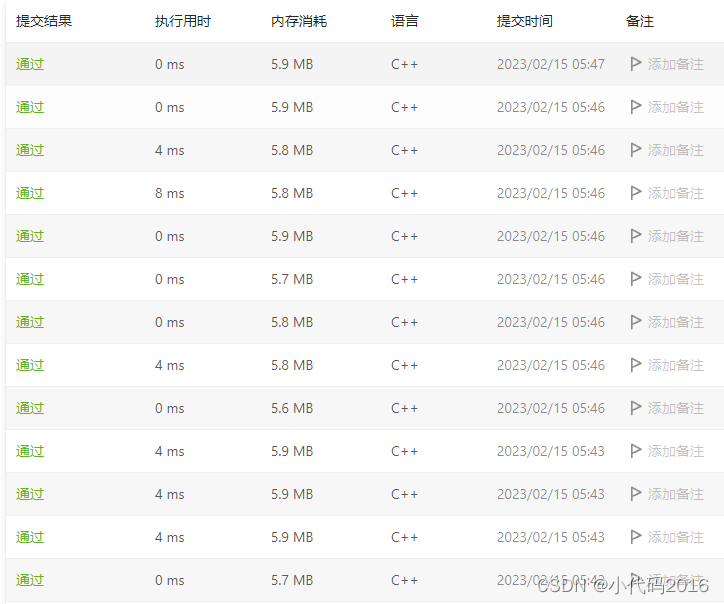
上述算法存在什么问题
- 没有处理前后空格
- 略丑陋
参考资料
高精度算法全套(加,减,乘,除,全网最详细)
大数加减乘除运算总结
Java BigDecimal详解
Java BigDecimal详解
Java中BigDecimal的8种舍入模式
Java中 DecimalFormat 用法详解

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容






所有评论(0)