行列式的定义及简单计算
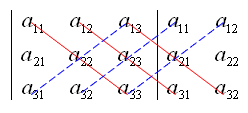
1. 三阶行列式的计算
·
- 行列式是一个数值,虽然形式上看起来比较复杂,比较不象数值;
- 将行列式可以转化为加减乘除的四则运算,同样也可以将四则运算转换为行列式的形式,这样转化的好处在什么呢,利用行列式的性质对其进行快速计算;
1. 三阶行列式的计算
2. 雅克比行列式到极坐标
从Jacobian矩阵、Hessian矩阵到Theano实现
雅可比行列式在积分坐标变换中的应用
Jn=∂(y1,y2,…,yn)∂(x1,x2,…,xn)=∣∣∣∣∣∣∣∣∣∣∂f1∂x1∂f2∂x1⋯∂fn∂x1∂f1∂x2∂f2∂x2⋯∂fn∂x2⋯⋯⋯⋯∂f1∂xn∂f2∂xn⋯∂fn∂xn∣∣∣∣∣∣∣∣∣∣
<script type="math/tex; mode=display" id="MathJax-Element-1"> J_n=\frac{\partial (y_1,y_2,\ldots,y_n)}{\partial(x_1,x_2,\ldots,x_n)}=\begin{vmatrix} \frac{\partial f_1}{\partial x_1}&\frac{\partial f_1}{\partial x_2}&\cdots&\frac{\partial f_1}{\partial x_n}\\ \frac{\partial f_2}{\partial x_1}&\frac{\partial f_2}{\partial x_2}&\cdots&\frac{\partial f_2}{\partial x_n} \\ \cdots&\cdots&\cdots&\cdots\\ \frac{\partial f_n}{\partial x_1}&\frac{\partial f_n}{\partial x_2}&\cdots&\frac{\partial f_n}{\partial x_n} \end{vmatrix} </script>
- 雅克比行列式的每一行表示多元函数关于各个成员的偏导数;
对于二重积分而言,设极坐标变换 x=ρcosθ,y=ρsinθ <script type="math/tex" id="MathJax-Element-2">x=\rho \cos\theta,y=\rho \sin\theta</script>,则其二阶行列式为:
∣∣∣cosθsinθ−ρsinθρcosθ∣∣∣=ρ
<script type="math/tex; mode=display" id="MathJax-Element-3"> \begin{vmatrix} \cos\theta & -\rho\sin\theta\\ \sin\theta&\rho\cos\theta \end{vmatrix}=\rho </script>
所以在积分运算中,便存在如下的变换形式:
∫∫Dxyf(x,y)dxdy=∫∫Dρ,θf[ρcosθ,ρsinθ]ρdρdθ
<script type="math/tex; mode=display" id="MathJax-Element-4"> \int\int_{D_{xy}}f(x,y)dxdy = \int\int_{D_{\rho,\theta}}f\left[\rho\cos\theta,\rho\sin\theta\right]\rho d\rho d\theta </script>
4. 计算
化简如下的表达式:
y=sin2xsin2ysin2z+sin(x+y)sin(y+z)sin(x+z)+sin(x+z)sin(y+z)sin(y+x)−sin(y+x)sin2zsin(x+y)−sin(y+z)sin(z+y)sin2x−sin(z+x)sin(x+z)sin2y
<script type="math/tex; mode=display" id="MathJax-Element-76"> \begin{split} y=&\sin 2x\sin 2y\sin 2z+\sin(x+y)\sin(y+z)\sin(x+z)+\\ &\sin(x+z)\sin(y+z)\sin(y+x)-\sin(y+x)\sin2z\sin(x+y)-\\ &\sin(y+z)\sin(z+y)\sin 2x-\sin(z+x)\sin(x+z)\sin2y \end{split} </script>
将其转化为行列式形式:
y==∣∣∣∣∣sin2xsin(y+x)sin(z+x)sin(x+y)sin2ysin(z+y)sin(x+z)sin(y+z)sin2z∣∣∣∣∣∣∣∣∣∣∣sinxcosx+sinxcosxsinycosx+sinxcosysinzcosx+sinxcoszsinxcosy+sinycosxsinycosy+sinycosysinzcosy+sinycoszsinxcosz+sinzcosxsinycosz+sinzcosysinzcosz+sinzcosz∣∣∣∣∣∣
<script type="math/tex; mode=display" id="MathJax-Element-221"> \begin{split} y=&\begin{vmatrix} \sin2x&\sin(x+y)&\sin(x+z)\\ \sin(y+x)&\sin2y&\sin(y+z)\\ \sin(z+x)&\sin(z+y)&\sin2z \end{vmatrix}\\ =&\begin{vmatrix}\\ \sin x\cos x+\sin x\cos x&\sin x\cos y+\sin y\cos x&\sin x\cos z+\sin z\cos x\\ \sin y\cos x+\sin x\cos y&\sin y\cos y+\sin y\cos y&\sin y\cos z+\sin z\cos y\\ \sin z\cos x+\sin x\cos z&\sin z\cos y+\sin y\cos z&\sin z\cos z+\sin z\cos z \end{vmatrix} \end{split} </script>
然后将行列式(两个方阵和的行列式)拆分为 6 个小行列式,其结果是十分清晰的,那就是 0.

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容





所有评论(0)