PBR的理论
GraphicsLab Project之基于物理的着色系统（Physical based shading）-直接光照

0 绪论

基于物理的渲染. 其本质就是根据物理世界中光与材质之间的交互方式.提出了一种方案模拟其效果.
其理论主要基于以下三个:

• 基于微平面(Microfacet)的表面模型
• 能量守恒
• 应用基于物理的BRDF

PBR 其实是一个光照模型.

在经典的光照模型中:

• 漫反射是 Lambert
• 镜面反射是 blinn-Phong
• 环境光是 c * (1-AO)

PBR:

• 漫发射是 Lambert/PI.
• 镜面反射是 Cook-Torrance.
• 环境光是 IBL (Image-Based Lighting).

PBR材质

1 反射方程

$$\begin{array}{l}{L}_o={\int }_{\Omega }f\left(p_i,w_i,w_o\right)L\left(p_i,w_i\right)n\cdot w_{i}d{w}_i\end{array}$$

$L_o$ : 表示经过着色之后 从 $w_o$方向观察点 p_i 时的颜色;
$f\left(p_i,w_i,w_o\right)$ : 表示的是点 $p_i$ 上，从 $w_o$ 方向反射出去的光照与从 $w_i$ 方向的入射的光照的比值，该函数称为BRDF（Bidirectional Reflection Distribution Function）.
$L_i$ : 表示从 $w_i$方向入射观察点 p_i 时的光照;
$n\cdot w_i$ : 表示入射光 $w_i$ 与 法线 $n$ 之间的关系.
${\int }_{\Omega }...d{w}_i$ : 表示在点 $p_i$ 法线方向上的半球，所有入射光线方向的积分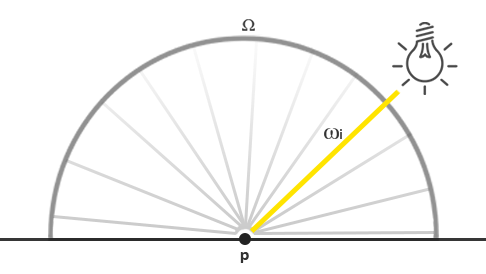

当光照射到物体表面. 分成两种反射的分量进行处理:

• 漫反射
• 镜面高光反射

将原先的BRDF函数分为了两个不同的部分：漫反射部分和镜面反射部分
反射方程可以等效为:
$$L_o={\int }_{\Omega }\left(f_d+f_s\right)L\left(p_i,w_i\right)n\cdot w_{i}d{w}_i$$

2 PBR之直接光照

在直接光照部分. 由于我们知道每一个光源的位置 / 方向 以及光照颜色.
针对单一光源有: 物体表面上同一个点只会从一个方向接受到来自光源的光照
所以可以用简单的叠加来避免积分的计算:
即有:
$$L_o=\left(f_d+f_s\right)L_i\left(n\cdot w_i\right)$$

2.1 漫反射

漫反射.它模拟的是从物体内部反射出去的光线效果.
Lambertian Reflection模型实际上假设物体内部反射出来的光线，是均匀的分布在半球上的，所以这种模型又被称之为Perfect Diffuse Reflection.

$$f_d=\frac{\mathrm{C}}{\pi }$$
其中:
$C$ : 表示 albedo贴图上采样得到的值

在经典光照模型中. 漫反射系数就是 albedo贴图采样得到的值.为什么PBR中多除了一个 $\pi$ 呢?

• 为了保证能量守恒

其实,实际上还乘了个 $k_d$

$k_d$ 的计算与镜面反射中 F的求解有关.

2.2 镜面反射

PBR的镜面反射是 Cook-Torrance镜面反射光照模型

$$\begin{array}{l}{f}_s=\frac{DFG}{4\left(w_i\cdot n\right)(w_o\cdot n)}\end{array}$$

D 法线分布函数 Normal Distribution Function(NDF)

这个函数描述的是:

• 微表面法线的分布.
• 当越多的微表面法线与宏观表面法线相近的时候. 高光区域会越亮. 区域越小. 反之. 高光区域会越暗. 区域越大.
• 这个函数返回的是一个标量

$$\begin{array}{l}ND{F}_{GGXTR}\left(n,h,a\right)=\frac{a^2}{\pi {\left({\left(n\cdot h\right)}^2\left(a^2-1\right)+1\right)}^2}\end{array}$$

其中.
$h$ : 表示 半程向量. 即 blinn-Phong 计算高光反射时候使用的半程向量. 即 $h=\frac{L+V}{|L+V|}$
$a$ : 表示 微表面的粗糙程度. 通过对粗糙纹理采样获得.

loat D_GGX_TR(vec3 N, vec3 H, float a)
{
    float a2     = a*a;
    float NdotH  = max(dot(N, H), 0.0);
    float NdotH2 = NdotH*NdotH;

    float nom    = a2;
    float denom  = (NdotH2 * (a2 - 1.0) + 1.0);
    denom        = PI * denom * denom;

    return nom / denom;
}

F 菲涅尔方程

F 表示 被反射的光线 所占的比率
这个比率会随着我们观察的角度不同而不同。
当光线碰撞到一个表面的时候，菲涅尔方程会根据观察角度告诉我们被反射的光线所占的百分比。
利用这个反射比率和能量守恒原则，我们可以直接得出光线被折射的部分以及光线剩余的能量。

$$\begin{array}{l}F\left(h,v,F_0\right)=F_0+(1-F_0)(1-h\cdot v{)}^5\end{array}$$

其中:
$h$ : 表示半程向量
$v$ : 表示观察向量
$F_0$ : 表示 表面的基本反射属性

F项描述的是镜面反射部分的比例，那么漫反射部分的比例自然就是1 - F了.
注意:

• 对于金属材质来说，只有镜面反射，没有漫反射。也就是说，这里的F项，需要区别对待金属材质和非金属材质
• 所以需要引入一个 金属材质 Metallic

对于 非金属材质 来说，我们就直接认定 $F_0$=0.04

vec3 fresnelSchlick(float cosTheta, vec3 F0)
{
    return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0);
}

vec3 F0 = vec3(0.04);
F0      = mix(F0, surfaceColor.rgb, metalness);
vec3 F = fresnelSchlick( max(HdotV,0.0),F0);

就是说F即镜面高光反射的部分.即 $K_s$
求可以求出 漫反射部分 $K_d$

vec3 kS = F;
vec3 kD = vec3(1.0) - kS;
kD *= 1.0 - metallic; 

G 几何函数

几何函数从统计学上近似的 求得了微平面间相互遮蔽的比率,这种相互遮蔽会损耗光线的能量.
几何函数采用一个材料的粗糙度参数作为输入参数,粗糙度较高的表面其微平面间相互遮蔽的概率就越高.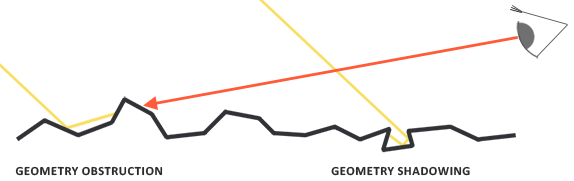

G项描述了 几何遮蔽 和 几何阴影 两种情况:

1. 观察方向（几何遮蔽(Geometry Obstruction)）
2. 光线方向向量（几何阴影(Geometry Shadowing)）

$$G\left(n,v,l,k\right)=G_{sub}(n,v,k)\cdot G_{sub}(n,l,k)$$

$$G_{SchlickGGX}\left(n,v,k\right)=\frac{n\cdot v}{\left(n\cdot v\right)(1-k)+k}$$

这里的k是α基于几何函数是针对直接光照还是针对IBL光照的重映射(Remapping) :

$$k_{direct}=\frac{(a+1{)}^2}{8}$$

$$k_{ibl}=\frac{a^2}{2}$$

float GeometrySchlickGGX(float NdotV, float k)
{
    float nom   = NdotV;
    float denom = NdotV * (1.0 - k) + k;

    return nom / denom;
}

float GeometrySmith(vec3 N, vec3 V, vec3 L, float k)
{
    float NdotV = max(dot(N, V), 0.0);
    float NdotL = max(dot(N, L), 0.0);
    float ggx1 = GeometrySchlickGGX(NdotV, k);
    float ggx2 = GeometrySchlickGGX(NdotL, k);

    return ggx1 * ggx2;
}

3 总结

直接光照的反射方程:
$$L_o=(k_d{f}_d+k_s{f}_s)L_i\left(w_i\cdot n\right)$$

• 其中 $k_s$ 和 $F$ 是一个东西. 只需要计算一次. 把打出来只是为了强调 能量守恒 这个关系.

最终的直接光照反射方程为:

$$L_o=(k_d\frac{C}{\pi }+\frac{DFG}{4\left(w_i\cdot n\right)\left(w_o\cdot n\right)})L_i\left(w_i\cdot n\right)$$

注意事项

PBR对计算空间的每个值是否为线性的有强烈的依赖性. 必须有:

1. HDR
2. Gamma校正

// base tone mapping
color = color / (color + vec3(1.0, 1.0, 1.0));
// gamma correction
color = pow(color, vec3(1.0 / 2.2, 1.0 / 2.2, 1.0 / 2.2));