0.概述

高级驾驶辅助系统（ADAS）领域，存在多种常用的坐标系：LiDAR 坐标系、车辆坐标系、相机坐标系、图像坐标系等。因为和这些坐标系频繁打交道，本文对点的旋转与坐标系旋转等变换给出直观推导与说明。

1.平移变换

1.1坐标系平移

1.2坐标点平移

2.旋转变换

2.1坐标系旋转变换

如下图所示，设原来的P点坐标为（x,y),表示为极坐标（r,α）

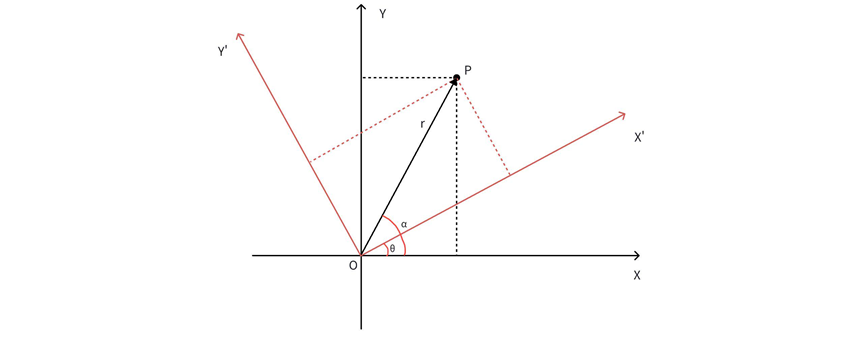
  则有如下关系式：

                                         

若将坐标系逆时针旋转角度θ，则原来的P点极坐标（r,α）→ （r, α-θ），则 

        

   表示为矩阵形式如下：

2.2坐标点旋转变换

如果是坐标系不变，只是坐标点绕原点逆时针旋转角度θ，如下图所示：

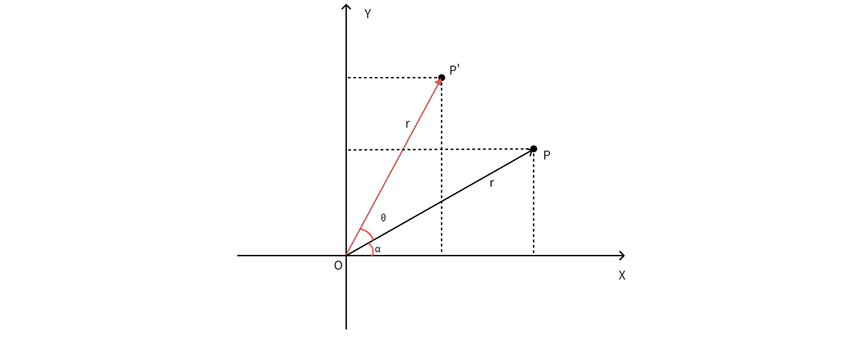
 在极坐标中表示为对应关系：

                ​​​​​​​        ​​​​​​​        ​​​​​​​                ​​​​​​​        

表示为原来的 P点坐标：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

表示为旋转变换后 P' 的坐标

                         

 表示为矩阵形式如下：

如果旋转中心不在原点，比如下图所示的A点（x0,y0)，

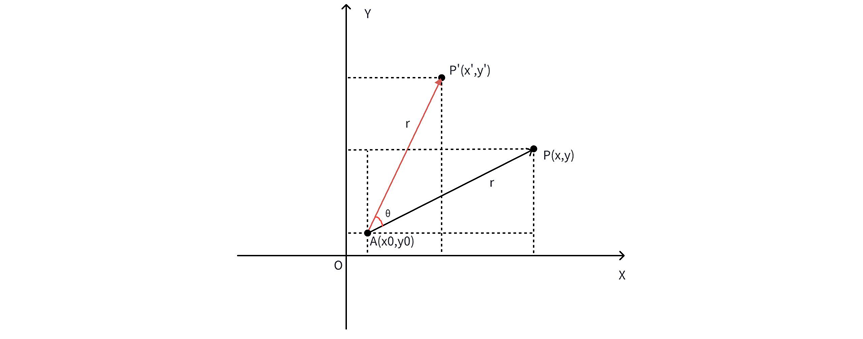
使用复数表示AP向量为：

则绕A点逆时针旋转θ角度后，得到 向量为：

展开得到：

由此根据AP向量与A点坐标，得到P’坐标为：

表示为矩阵形式如下：

代码实现如下：

""" data point coordinate transformation"""
def trans_curr_bevroi_to_large_img(
    curr_bevroi_corner_input,
    ego_pose,
    yaw,
    vcs_bevroi_range_x,
    vcs_bevroi_range_y,
    ego_and_center_dist,
):
    """
    curr_bevroi_corner: In the current frame, the corner point of the perception ROI at the center of the vehicle 
    ego_pose: In the current frame, the pose of the vehicle 
    yaw: angle of deviation from the starting point [x-axis]
    vcs_bevroi_range_x: vcs bevroi perception range in x-axis
    vcs_bevroi_range_y: vcs bevroi perception range in y-axis
    ego_and_center_dist: the dist of ego pose and the geometric center of current perception roi

    """
    curr_bevroi_corner = copy.deepcopy(curr_bevroi_corner_input)
    center_point_x = ego_pose[0] + ego_and_center_dist * math.cos(yaw)
    center_point_y = ego_pose[1] + ego_and_center_dist * math.sin(yaw)
    curr_bevroi_corner[0] -= vcs_bevroi_range_x / 2.0
    curr_bevroi_corner[1] -= vcs_bevroi_range_y / 2.0
    curr_bevroi_corner[0] += center_point_x
    curr_bevroi_corner[1] += center_point_y

    corner_point_trans_x = (
        (curr_bevroi_corner[0] - center_point_x)  * math.cos(yaw)
        -(curr_bevroi_corner[1] - center_point_y) * math.sin(yaw)
        + center_point_x
    )
    
    corner_point_trans_y = (
        (curr_bevroi_corner[0] - center_point_x) * math.sin(yaw)
        + (curr_bevroi_corner[1] - center_point_y)* math.cos(yaw)
        + center_point_y
    )
    return [round(corner_point_trans_x), round(corner_point_trans_y)]

3.复合变换

4.相机坐标系变换

5.Lidar与视觉坐标系转换