举个例子，假如要在一个地区进行1000人的疾病检测，我们站在上帝视角，知道这1000人中，有10人是疾病感染者，占比1%。

但实际的检测结果可能存在误差，误差包括两种情况

1. 疾病感染者，被错误诊断为健康
2. 身体健康，但却被错误诊断为感染者

对应了两种情况

1. 检测出来的是阴性，就一定没有问题么?
2. 检测出来阳性，就真的是阳性吗？

如上两种情况都属于误诊，需要用到贝叶斯公式来回答.

检测结果如下：

1. 9名感染者得到了正确的阳性结果(TP,true positive)，1人出现假阴性(FN,false negative).
2. 其余990位健康的人中，检测除了89为假阳性(FP,false positive).901人得到了正确的阴性结果（TN,true negative)

图形化表示是这个样子的：

列成表格表示如下：

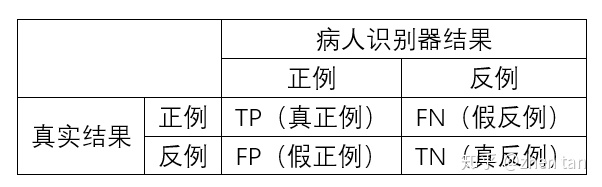
真实情况	预测为阳性	预测为阴性	召回率
阳性患者	9人(True Positive,TP)	1人(False Negative,FN)
健康人员	89人(False Positve, FP)	901人(True Negative, TN)
准确率

分析流程如下:

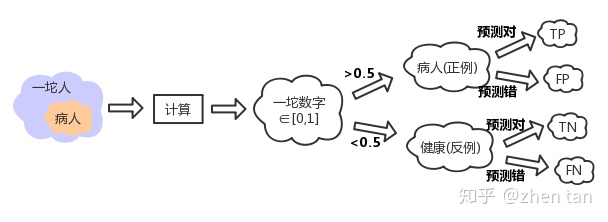
根据以上的分析，我们总结如下：

• TP、True Positive   真阳性：预测为正，实际也为正
• FP、False Positive  假阳性：预测为正，实际为负
• FN、False Negative 假阴性：预测与负、实际为正
• TN、True Negative 真阴性：预测为负、实际也为负
• 样本总数=TP+FN+FP+TN
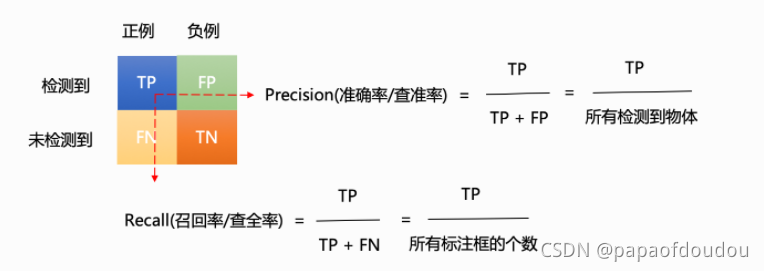
• 准确率表示的是在预测结果中，有多少是真正的阳性
• 召回率表示的是在所有的阳性样本中，你究竟找回来几个？猜对了多少？

TP/FP/FN/TN组合，第一个字母表示算法预测的对错，也就是是否和实际情况相符，T表示正确，F表示错误。第二个字母表示算法预测的结果，P为正例，N为负例.

---

       以上的分析中，我们实际上是使用了被称为混淆矩阵的数学工具， 混淆矩阵也被称为混淆表，是表示分类器的预测值和实际结果（标签）之间关系的，由行和列构成的表。我们用这个表更好的理解模型或分类器的实现。

除了准确率，还有一个概念叫做准确度，它描述的是测量值与真实值的接近程程度，公式是：

      

以上面的新冠筛查为例，准确度为：

既然有了准确度，是不是还可以定义一个错误度:

错误率度为：

  

准确率和召回率是相互影响的，理想情况下肯定是两者都高，但是一般情况下准确率高，召回率就低；召回率高，准确率就低；如果两者都低，那肯定是什么环节有问题了。

       比如，在检索系统中，如果希望提高召回率，即希望更多的相关文档被检索到，就要放宽“检索策略”，便会在检索中伴随出现一些不相关的结果，从而影响到准确率。如果希望提高准确率，即希望去除检索结果中的不相关文档时，就需要严格“检索策略”，便会使一些相关文档不能被检索到，从而影响到召回率。

      针对不同目的，如果是做搜索，那就是优先提高召回率，在保证召回率的情况下，提升准确率；如果做疾病监测、反垃圾，则是优先提高准确率，保准确率的条件下，提升召回率。

大样本上看，无论是病人分布还是健康人群的分布，都符合正太分布，所以，一种划分如下：

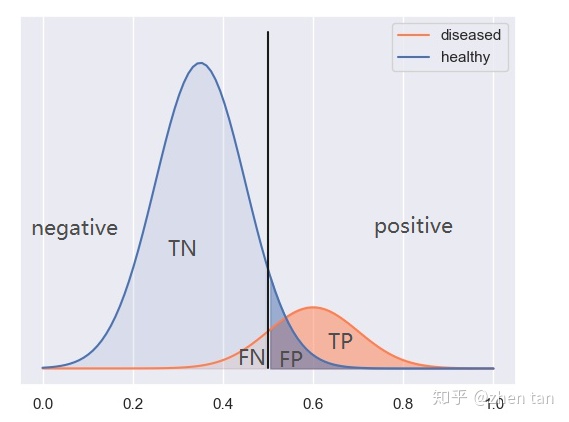
参考资料：

P-R曲线和ROC曲线理解 - 知乎

https://blog.csdn.net/tugouxp/article/details/120624088https://blog.csdn.net/tugouxp/article/details/120624088

AP和mAP的计算

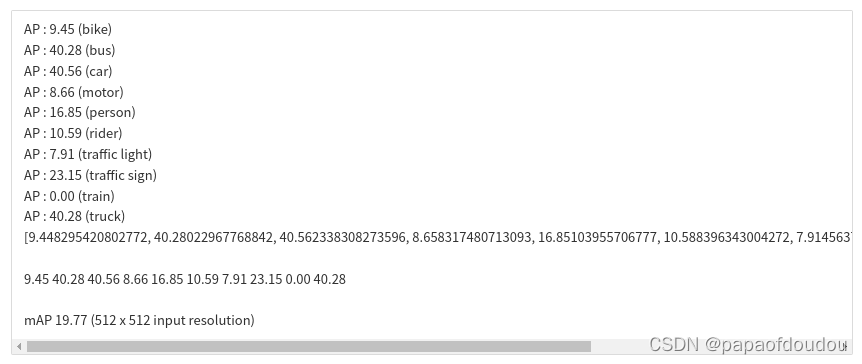
（9.45+40.28+40.56+8.66+16.85+10.59+7.91+23.15+0.00+40.28）/ 10= 19.773

结束！