机器学习练习题
例1:解:例1:解:例1:解:例1:
例1:

解:
最大似然估计:
P(男)=8/20=0.4,P(女)=12/20=0.6P(男)= 8/20=0.4,P(女) = 12/20 = 0.6P(男)=8/20=0.4,P(女)=12/20=0.6
argmax∏i=1n(Pi)=ln∏i=1nPi=ln∏i=1n12πρexp(−(xi−μ)22ρ2)=nln12πρ−∑i=1n(xi−u)22ρ2argmax \prod _{i = 1} ^ n(P_i) = \ln \prod_{i=1}^n P_i = \ln \prod_{i=1}^n \frac{1}{\sqrt {2 \pi} \rho} exp(-\frac{(x_i - \mu)^2}{2\rho^2}) =\\ n \ln \frac{1}{ \sqrt {2 \pi } \rho} - \sum_{i=1}^n \frac{(x_i - u)^2}{2 \rho^2}argmaxi=1∏n(Pi)=lni=1∏nPi=lni=1∏n2πρ1exp(−2ρ2(xi−μ)2)=nln2πρ1−i=1∑n2ρ2(xi−u)2
对u求导并令导数为0得:
∑i=1n(xi−u)ρ2=0\sum_{i=1}^n \frac{ (x_i - u) }{\rho^2}= 0i=1∑nρ2(xi−u)=0
即:
1n∑i=1nxi=μ\frac{1}{n}\sum _{i=1}^nx_i = \mun1i=1∑nxi=μ
同理可得:
ρ2=1n∑i=1n(xi−u)2\rho ^2 = \frac{1}{n} \sum_{i=1}^n (x_i - u)^2ρ2=n1i=1∑n(xi−u)2
例2:

解:
例3:
解:
公式: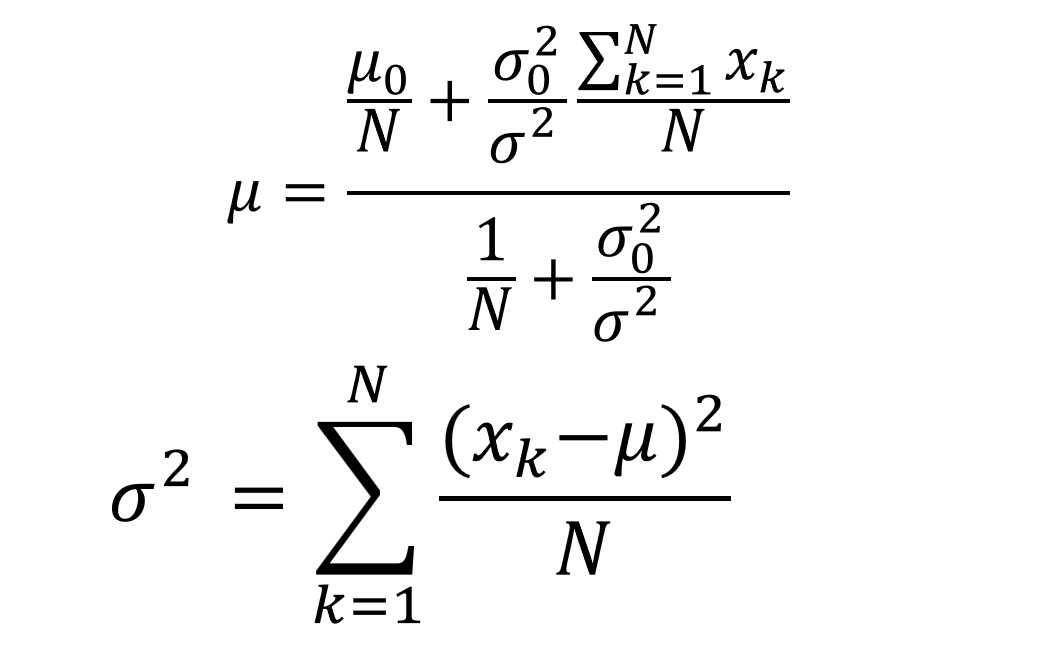




DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容






所有评论(0)