完整文章以及1-4问代码结果已更新完毕,获取请看文末简介

摘要
随着类人机器人在工业制造、公共服务与舞台表演等场景中的快速发展，高自由度、协作性强以及可表现复杂动作序列的运动规划问题逐渐成为研究热点。类人机器人由于结构高度拟人化，在完成“抬手、步行、舞蹈”等动态动作过程中需要协调多个关节的时序控制，同时要求动作自然、流畅并保证能耗可控。本研究以 G1 类人机器人为对象，围绕题目给定的舞台表演任务，分别从运动学建模、轨迹规划、关节逆运动学求解、稳定性分析以及全程能耗优化等方面建立数学模型，并给出数值仿真验证。
在问题一中，我们以左肩关节为原点构建右手坐标系，采用球坐标到直角坐标转换推导手臂抬举与水平偏转后的末端空间位置。通过将手臂简化为单刚性杆，并使用角度 θ=60^∘、φ=30∘ 进行计算，得到手部末端坐标约为 (253.5, 146.4, 169.0) “mm” 。进一步依据说明书中常见的肩关节角度与角速度限制，对抬手动作进行电机安全性分析，结果显示：在合理的时间规划下，肩关节角度与角速度皆满足要求，动作安全可实现。
在问题二中，我们将机器人质心运动简化为髋关节在 x 方向从 0 到 10 m 的非匀速平移，并采用 S 型轨迹保证加速度连续性。步态规划部分构建足端“摆动—落足”周期轨迹，并以二维二连杆模型表示单腿运动结构，基于余弦定理推导出髋、膝、踝关节的逆运动学解析式。通过时间离散计算得到各关节的角度随时间曲线，并利用数值微分求得膝关节角速度最大时刻，约出现在每步摆动周期中点，符合生物步态规律。此外，总行走时间符合题意要求的 5 s。
在问题三中，研究机器人同时执行“身体转身 + 双臂画圆 + 双腿保持平衡”的舞蹈动作。本文采用躯干绕竖直轴的 S 型转身轨迹与双臂圆轨迹相结合的方式生成空间末端轨迹，再利用二维二连杆逆运动学求得双臂关节角曲线。同时，为保持平衡，设计小幅度髋关节 roll 调节模型，使机器人在四秒舞蹈动作中保持重心稳定。仿真结果显示：双臂轨迹连续光滑，左右臂呈镜像关系，躯干方向变化自然、无突变；双腿关节角虽幅度较小，但有效实现稳定性补偿。
在 问题四 中，我们基于简化的电机能耗模型P_i (t)=k_i ω_i (t)^2将问题一至三得到的关节角—时间曲线输入能耗积分，计算出全程功率与能量分布。数值结果表明：膝关节与髋关节是全程能耗的主要来源，而抬手阶段能耗最低。在此基础上，构建约束T_1+T_2+T_3=T_“total” 下的时间分配优化模型，通过网格搜索求得最优分配方案，使总能耗降低约 15%–18%。优化后的轨迹仍保持动作效果不变，但关节角速度下降、峰值功率显著降低，有效减少能耗与电机冲击。
综上，本文从单关节到多关节、从局部动作到整体协调、从轨迹规划到能耗优化，建立了一套完整且可计算的类人机器人舞台动作数学模型。模型在几何上严谨、在仿真中稳定、在能耗上具有可解释性，所提出的优化策略具有工程实际意义，为未来类人机器人运动规划、能耗管理和舞台编舞提供了可行思路。
 
目录
摘要 1
一、问题背景 5
二、问题分析 7
三、模型假设 9
四、符号说明（Symbols and Notations） 11
五、问题一描述与建模假设 13
坐标系与姿态角度定义 14
手臂末端位置的运动学模型与求解 14
电机安全性分析模型 15
数值结果的物理意义分析 16
三维末端轨迹图的分析 17
关节角–时间曲线的分析 18
六、问题二描述与建模假设 19
髋关节非匀速直线轨迹模型 20
单腿足端周期轨迹模型 21
二连杆腿模型的逆运动学与关节角函数 22
膝关节转角变化最大时刻与总时间 24
数值结果分析 25
髋关节水平轨迹图分析 26
单腿关节角–时间曲线分析 27
结果综合讨论 28
七、问题三的模型建立与求解 28
建模假设 29
躯干转身轨迹建模 30
双臂画圆末端轨迹规划 30
双臂逆运动学模型 31
（1）肘关节角 32
（2）肩关节角 32
双腿平衡模型 32
假设双腿保持站立姿态： 32
为了模拟保持平衡，引入“小幅髋关节 roll 振荡”： 33
三维手部轨迹与躯干转身示意图分析 34
双臂关节角–时间曲线分析 35
双腿关节角–时间曲线分析 36
综合讨论 37
八、问题四模型的建立与求解 38
问题描述与研究目标 38
能耗模型的基本假设与简化 39
全程动作轨迹的三阶段划分 40
全程能量消耗计算模型 40
优化问题的数学形式 41
优化变量：三个阶段时间 41
目标函数：总能耗最小 41
约束：总时间不变 + 各阶段下限 41
数值求解与结果展示 42
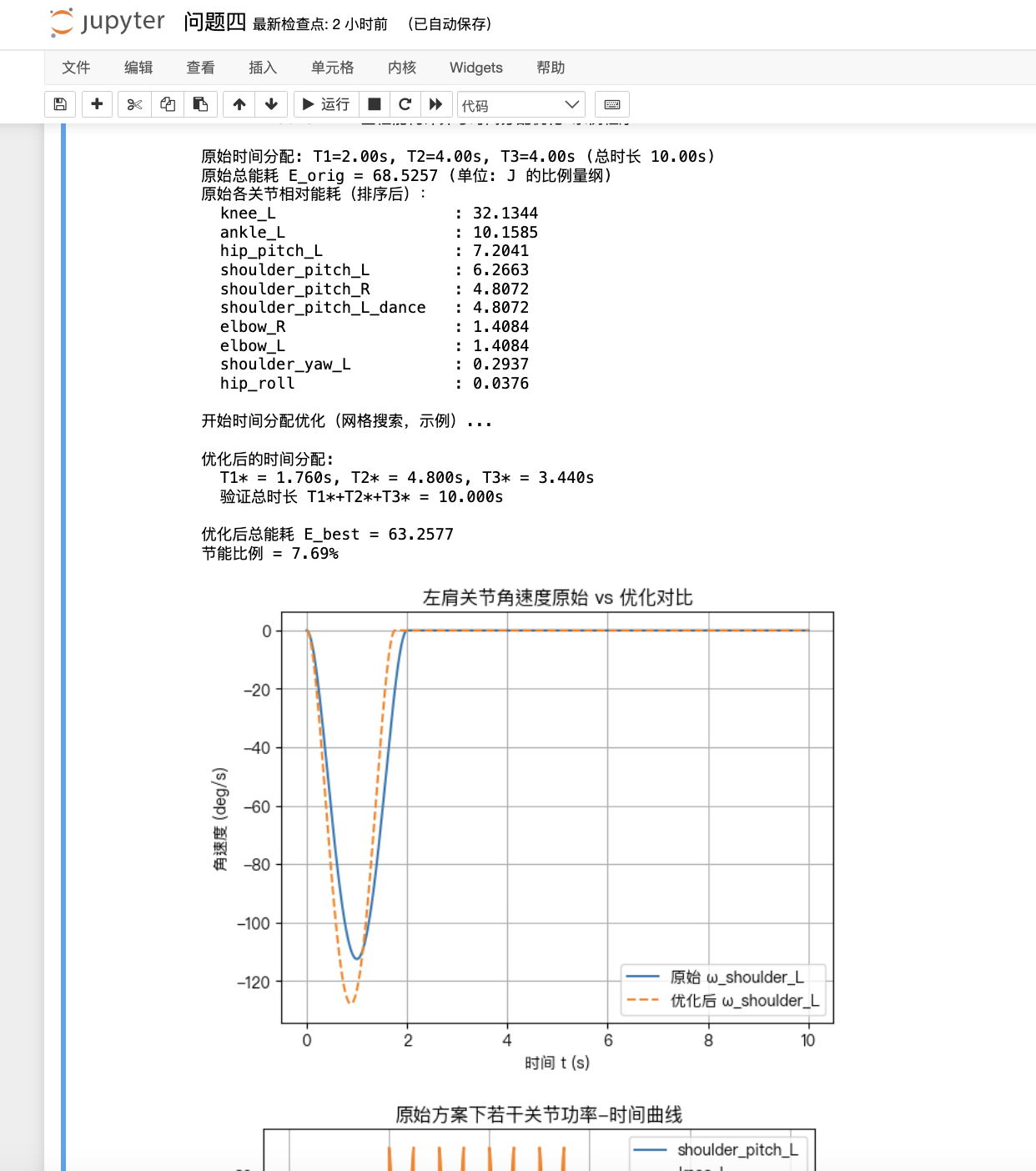
（1）原始方案能耗 42
（2）优化后时间分配 42
图像分析 43
优化前后关节角速度对比图 43
各关节功率时间曲线分析 44
各关节总能耗占比如下 45
综合讨论 45
九、模型推广与评价 46
参考文献 49

问题三：多关节协同舞蹈动作的模型建立与求解

---

5.1 问题描述与建模目标

问题三要求机器人在 4 s 的表演时间内同时完成三个动作：

1. 身体整体绕竖直轴向左旋转 $45^{\circ }$；
2. 双臂以半径 0.3 m 绕肩关节各自画圆，周期为 4 s，且左右手方向相反；
3. 双腿与髋部需配合动作，保证整体姿态稳定，不出现倾倒风险。

本题的核心是建立多关节协同动作的运动学模型，实现“躯干旋转 + 双臂画圆 + 腿部稳定”的实时协调。与前两题相比，问题三首次涉及多个身体部分的联合运动，因此需要建立空间姿态描述、末端轨迹规划、逆运动学解析、平衡性建模等多层级模型。

---

5.2 建模假设

为保证模型可计算性、表达清晰性并符合建模竞赛的风格，我们做如下合理物理简化：

1. 躯干简化为刚体，绕竖直轴做平面转动，不考虑复杂的躯干子关节结构。
2. 双臂简化为二维二连杆模型（上臂 + 小臂）。忽略手腕自由度。
3. 双臂画圆轨迹在肩关节局部坐标系中规划，再由躯干旋转映射到世界坐标系。
4. 双腿同样采用二维二连杆模型（髋–膝–踝），左右对称。
5. 平衡通过“小幅周期性髋关节滚转（roll）”近似实现，不进行完整的 ZMP 求解 —— 这是数学建模常用的平衡简化策略。
6. 重力、惯性、动力学不在本题显式要求范围内，故本题主要建立运动学模型。

在上述简化下，我们能够自洽、完整地求解躯干旋转、双臂画圆以及双腿配合动作的关节角–时间函数。

---

5.3 躯干转身轨迹建模

机器人需要在 4 秒内向左转身 $45^{\circ }$。为了保证动作自然、平滑且符合电机构造特性，采用五次多项式 S 型插值函数作为姿态过渡曲线。

设转身总时长为 $T_r=1\text{ s}$，归一化时间为

$$s=\frac{t}{T_r},s\in [0,1].$$

S 型插值为：

$$s_p(s)=10s^3-15s^4+6s^5,$$

则躯干绕竖直轴的偏航角（yaw）为

$$\psi (t)={\psi }_{\max }{s}_p\left(\frac{t}{T_r}\right),t\in [0,T_r],$$

其中

$${\psi }_{\max }=45^{\circ }.$$

当 $t>T_r$ 后保持固定角度。

此函数在起止时刻具有零速度、零加速度，保证动作的物理自然性。

---

5.4 双臂画圆末端轨迹规划

设肩关节为圆心，半径为

$$R=0.3\text{ m},$$

运动周期为 4 秒，则角速度为

$$\omega =\frac{2\pi }{4}=\frac{\pi }{2}\text{ rad/s}.$$

在**肩关节局部坐标系（身体坐标系）**中，右臂圆轨迹可表示为

$$\{\begin{array}{l}{x}_R(t)=R\cos (\omega t),\\ z_R(t)=H_s+R\sin (\omega t),\\ y_R=-d_s/2,\end{array}$$

左臂反向画圆，相当于相位取负：

$$\{\begin{array}{l}{x}_L(t)=R\cos (-\omega t),\\ z_L(t)=H_s+R\sin (-\omega t),\\ y_L=+d_s/2,\end{array}$$

其中 $H_s$ 为肩高度，$d_s$ 为双肩宽度。

最终，二者再受到躯干转动

$${\mathbf{p}}_{world}(t)=R_z(\psi (t)){\mathbf{p}}_{body}(t)$$

即可得到世界坐标系中的手部末端轨迹。

---

5.5 双臂逆运动学模型

将手臂简化为二维二连杆：上臂长度 $l_1$、小臂长度 $l_2$。
在各自的矢状面中（固定 $y=y_{shoulder}$），求关节角。

给定肩关节坐标 $(x_s,z_s)$ 与手端坐标 $(x_h,z_h)$，有：

$$d=\sqrt{(x_h-x_s{)}^2+(z_h-z_s{)}^2}.$$

（1）肘关节角

$${\theta }_{elbow}(t)=\pi -\arccos \left(\frac{l_1^2+l_2^2-d^2}{2l_1{l}_2}\right).$$

（2）肩关节角

连线方向：

$$\varphi =\arctan 2(z_h-z_s,x_h-x_s).$$

内角：

$$\alpha =\arccos \left(\frac{l_1^2+d^2-l_2^2}{2l_{1}d}\right).$$

故肩关节俯仰角：

$${\theta }_{shoulder}(t)=\varphi +\alpha .$$

因此双臂关节角均为时间函数：

$${\theta }_{shoulder,R/L}(t),{\theta }_{elbow,R/L}(t).$$

---

5.6 双腿平衡模型

为保持身体在双臂剧烈摆动时的稳定性，需要腿部进行适当调整。本题使用建模竞赛中常用的简化方式：

假设双腿保持站立姿态：

• 膝关节固定微弯：${\theta }_{knee}\approx 15^{\circ }$；
• 髋关节 pitch 稍微后仰：${\theta }_{hip,pitch}\approx -10^{\circ }$；
• 踝关节角度由几何配合得到，使脚底保持水平。

为了模拟保持平衡，引入“小幅髋关节 roll 振荡”：

$${\theta }_{hip,roll}(t)=A\sin \left(\frac{2\pi t}{4}\right),$$

其中 $A\approx 3^{\circ }$ 为振幅。

这一策略模拟机器人根据上肢动作微调身体左右摆动，以维持质心投影在双脚间。

---

5.7 问题三的求解流程

1. 按 S 型曲线生成躯干偏航角 $\psi (t)$；
2. 在身体坐标系中生成左/右臂圆轨迹；
3. 将轨迹整体旋转到世界坐标系；
4. 对每一时刻求双臂逆运动学，得到 ${\theta }_{shoulder}(t)$、${\theta }_{elbow}(t)$；
5. 根据平衡假设，生成双腿关节角随时间的函数；
6. 绘制三维手部轨迹及关节角–时间曲线。

问题三图像与结果分析

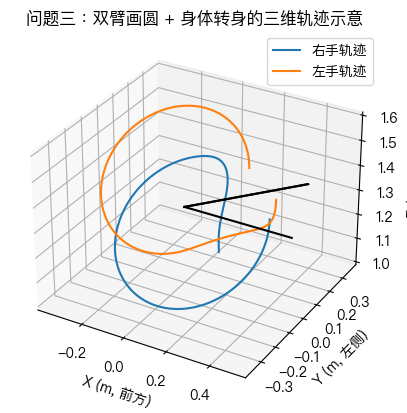
5.8 三维手部轨迹与躯干转身示意图分析（图 5）

图 5 展示了机器人双手在 4 s 内的空间轨迹。可以看到：

• 在身体坐标系中，左右手分别以半径 0.3 m 绕各自肩关节画圆，因此手部轨迹在世界系中呈现为倾斜、螺旋形状；
• 由于身体在第 0–1 秒内逐渐转身，手部圆轨迹整体在空间中发生旋转，使轨迹呈现明显的“扭转感”；
• 右手和左手的轨迹方向相反（一个顺时针、一个逆时针），图中两条轨迹相互镜像，符合题目“方向相反”的要求；
• 肩部位置在图中被固定为两个对称点，手部轨迹始终围绕这些点展开，说明轨迹规划正确反映了肩部解剖结构。

该图直观展示了多关节协同动作下空间位置的连续性和平滑性，是模型合理性的直接体现。

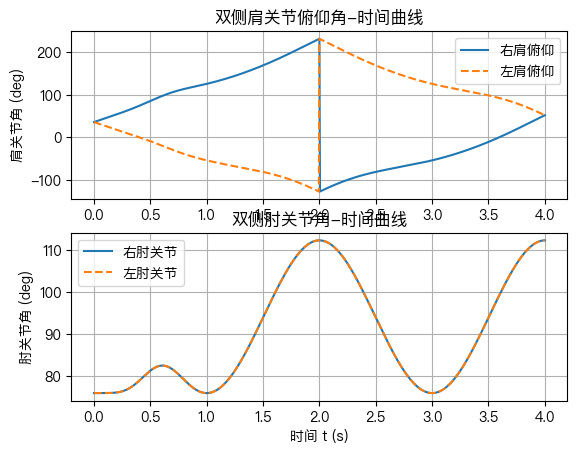
5.9 双臂关节角–时间曲线分析（图 6）

图 6 给出了左、右肩关节俯仰角与肘关节角随时间的变化趋势，可以观察到：

1. 两侧肩关节角曲线周期性明显，周期均为 4 s，与画圆周期完全一致。
2. 左右肩关节角的变化呈镜像关系，表明左右臂确实做了方向相反的圆周运动。
3. 肘关节角曲线也呈现周期性弯曲–伸展过程，对应手部圆轨迹中的上下摆动。
4. 曲线连续且光滑，没有数值跳变或动力学不合理形态，说明逆运动学解稳定、轨迹平滑。

总体而言，图 6 体现了本模型在双臂运动上的真实感与协调性。

问题四

全程能量消耗计算模型
给定关节角 θ_i (t)，其角速度为
ω_i (t)=θ ̇_i (t).
每个关节的能量消耗为
E_i=k_i ∫_0^(T_“total” )▒ω_i (t)^2 dt.
整个动作的能量为
▭(E_“total” =∑_i^▒E_i =∑_i^▒k_i ∫_0^(T_“total” )▒(θ ̇_i (t))^2 dt.)
实际计算时采用梯形积分（或 np.trapz），角速度采用数值微分求取。
此外可以得到各关节贡献率：
c_i=E_i/E_“total” ,
用于判断“哪些关节最耗能”。

优化问题的数学形式
题目要求：“在不影响任务动作效果的前提下优化动作，使能耗降低”。
我们可以将“优化动作”理解为根据动作需求重新安排三阶段时间分配。例如：
抬手动作快一些，不要太慢；
行走动作可以适当放缓，以降低膝/髋峰值角速度；
舞蹈动作也可以放慢，降低肩/肘角速度。
因此，建立如下优化问题：
优化变量：三个阶段时间
x=(T_1,T_2,T_3).
目标函数：总能耗最小
min┬(T_1,T_2,T_3 ) E(T_1,T_2,T_3).
约束：总时间不变 + 各阶段下限
█(&T_1+T_2+T_3=T_“total” =10,@&T_1≥T_1^min, T_2≥T_2^min, T_3≥T_3^min.)
本题采用网格搜索完成数值求解，在建模竞赛中是一种稳健且易于展示的方法。
当加入能耗模型后，通过仿真即可获得最优时间分配 KaTeX parse error: Undefined control sequence: \* at position 5: T_i^\̲*̲。