MATLAB仿真UR5机器人simulink simscape 自制建模 正向运动学，逆向运动学 关节空间轨迹规划 五次多项式轨迹规划 笛卡尔空间轨迹规划 直线插补 还包含机器人工具箱建立的模型对比

在机器人研究领域，MATLAB是一款极为强大的工具，它提供了丰富的函数库和仿真环境，能让我们对机器人的运动学和轨迹规划进行深入的研究与分析。今天咱们就来聊聊利用MATLAB的Simulink和Simscape对UR5机器人进行自制建模，并探索其正向运动学、逆向运动学，以及关节空间和笛卡尔空间的轨迹规划，同时对比使用机器人工具箱建立的模型。

一、UR5机器人自制建模

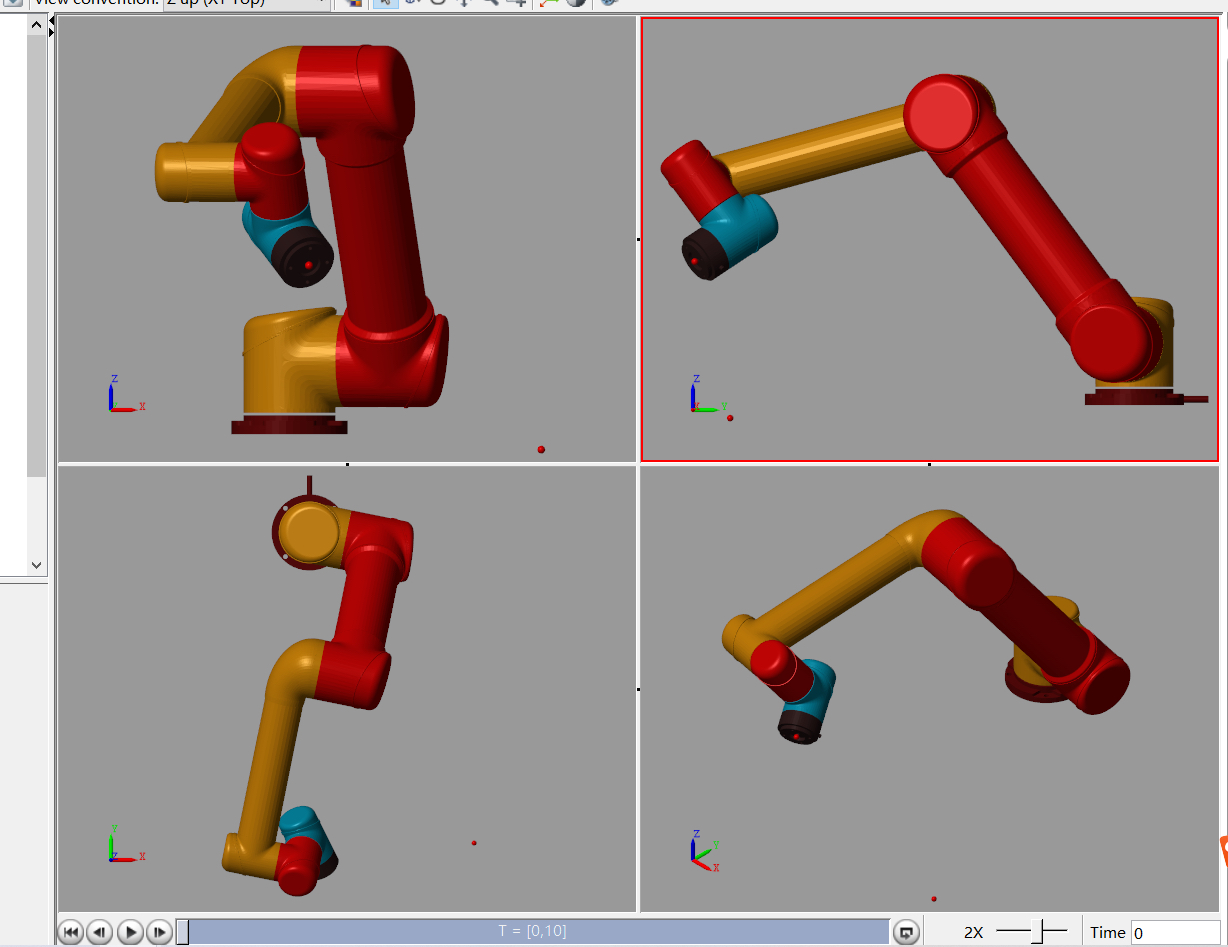
1. Simscape建模

Simscape是MATLAB中用于多领域物理系统建模和仿真的工具包。在对UR5机器人建模时，我们可以利用Simscape中的机械元件库来搭建机器人的结构。

% 假设我们已经在Simscape中搭建好了UR5机器人模型，以下是对模型部分参数的设置
model = 'ur5_simulink_model';
open_system(model);
% 获取模型中的某个关节的参数并修改
joint = get_param([model,'/Joint1'],'Position');
set_param([model,'/Joint1'],'Position', joint + 0.1);

上述代码首先打开已经搭建好的UR5机器人Simulink模型，然后获取名为Joint1的关节位置参数，并对其位置增加0.1弧度。通过这样的方式，我们可以在模型搭建完成后对其各个关节的参数进行灵活调整，以适应不同的仿真需求。

2. 运动学建模基础

UR5机器人有6个关节，要理解其运动学，我们得先明白正向运动学和逆向运动学。

二、正向运动学与逆向运动学

1. 正向运动学

正向运动学就是已知机器人各个关节的角度，求解末端执行器的位置和姿态。在MATLAB中，我们可以通过齐次变换矩阵来实现。

% 假设已经定义了6个关节角度q1 - q6
q1 = pi/4; q2 = pi/6; q3 = pi/8; q4 = pi/10; q5 = pi/12; q6 = pi/14;
% 定义UR5机器人的连杆参数
a = [0, -0.425, -0.3922, 0, 0, 0];
d = [0.089159, 0, 0, 0.10915, 0.09465, 0.0823];
alpha = [pi/2, 0, 0, pi/2, -pi/2, 0];
% 计算各个关节的齐次变换矩阵
T1 = trotz(q1) * transz(d(1)) * transx(a(1)) * trotx(alpha(1));
T2 = trotz(q2 + pi/2) * transz(d(2)) * transx(a(2)) * trotx(alpha(2));
% 以此类推计算T3 - T6
% 末端执行器的齐次变换矩阵
T = T1 * T2 * T3 * T4 * T5 * T6;

上述代码通过定义连杆参数和关节角度，利用齐次变换的函数trotz（绕z轴旋转）、transz（沿z轴平移）、transx（沿x轴平移）和trotx（绕x轴旋转）来计算每个关节的齐次变换矩阵，最后将它们相乘得到末端执行器的齐次变换矩阵T，这个矩阵就表示了末端执行器在空间中的位置和姿态。

2. 逆向运动学

逆向运动学则是已知末端执行器的位置和姿态，求解各个关节的角度。这通常是一个更为复杂的问题，因为可能存在多组解。在MATLAB中，我们可以通过数值迭代的方法来求解。

% 假设已知末端执行器的期望位姿T_desired
T_desired = [1 0 0 0.5; 0 1 0 0.3; 0 0 1 0.2; 0 0 0 1];
% 初始猜测的关节角度
q0 = [0 0 0 0 0 0];
% 利用fmincon函数进行数值迭代求解
options = optimoptions('fmincon','Display','iter');
q_sol = fmincon(@(q) norm(forward_kinematics(q) - T_desired), q0, [], [], [], [], [-pi,-pi,-pi,-pi,-pi,-pi], [pi,pi,pi,pi,pi,pi],[],options);
function T = forward_kinematics(q)
    % 这里按照正向运动学的计算方式，根据q计算T
    % 代码省略，与前面正向运动学计算类似
end

上述代码利用fmincon函数，以正向运动学计算得到的末端执行器位姿与期望位姿的误差最小为目标，通过不断迭代调整初始猜测的关节角度q0，最终得到满足期望位姿的关节角度解qsol。这里定义了一个内部函数forwardkinematics来进行正向运动学的计算，作为fmincon函数的目标函数。

三、轨迹规划

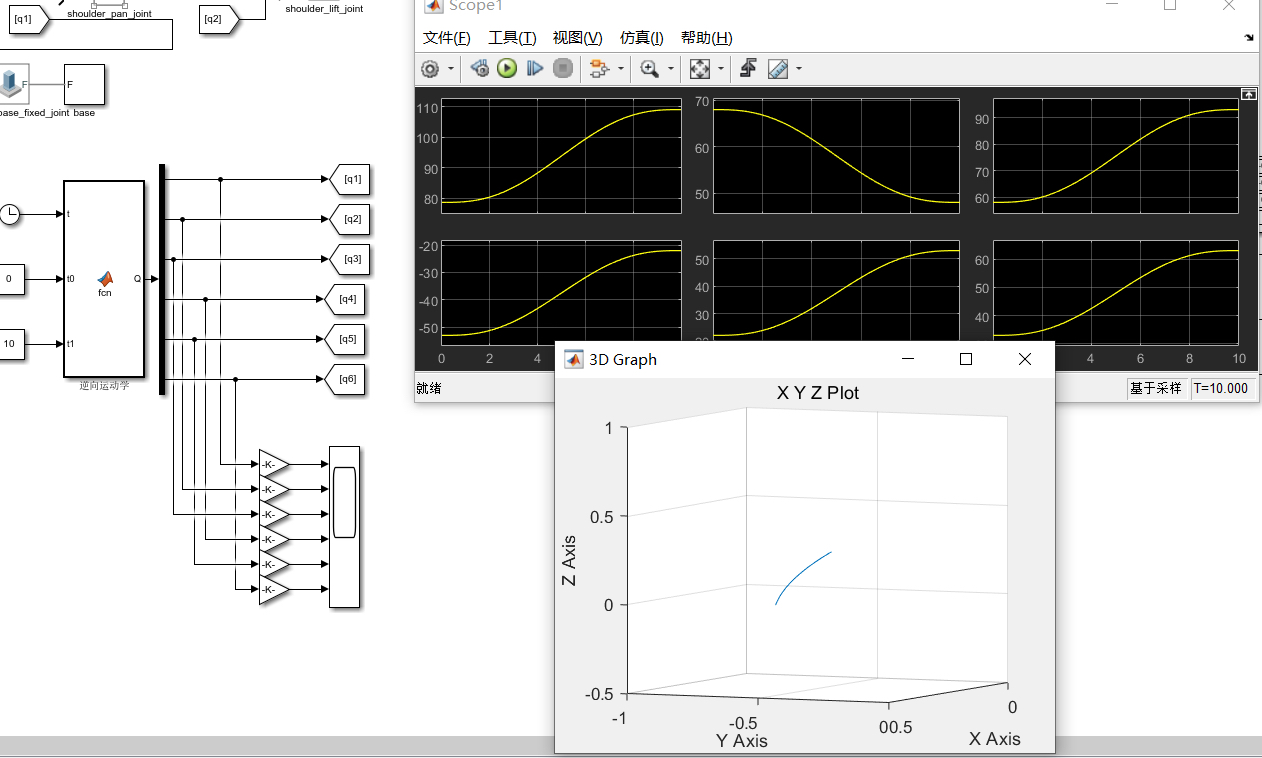
1. 关节空间轨迹规划 - 五次多项式轨迹规划

在关节空间进行轨迹规划时，五次多项式轨迹规划能够保证加速度的连续性，使机器人运动更加平滑。

% 起始关节角度
q_start = [0 0 0 0 0 0];
% 目标关节角度
q_end = [pi/2 pi/3 pi/4 pi/5 pi/6 pi/7];
% 运动时间
t_start = 0;
t_end = 5;
t = linspace(t_start, t_end, 100);
% 计算五次多项式系数
a0 = q_start;
a1 = 0;
a2 = 0;
a3 = (20*(q_end - q_start))/(t_end - t_start)^3;
a4 = (-30*(q_end - q_start))/(t_end - t_start)^4;
a5 = (12*(q_end - q_start))/(t_end - t_start)^5;
% 计算各个时刻的关节角度
q = a0 + a1*(t - t_start) + a2*(t - t_start).^2 + a3*(t - t_start).^3 + a4*(t - t_start).^4 + a5*(t - t_start).^5;

上述代码首先定义了起始和目标关节角度，以及运动时间范围。然后通过五次多项式的系数计算公式得到各个系数a0 - a5，最后根据时间向量t计算出每个时刻对应的关节角度q，这样就规划出了一条在关节空间内从起始位置到目标位置的平滑轨迹。

2. 笛卡尔空间轨迹规划 - 直线插补

笛卡尔空间轨迹规划关注的是末端执行器在笛卡尔坐标系中的运动。直线插补是一种常见的方法，让末端执行器沿着直线从起始点运动到目标点。

% 起始位置
p_start = [0 0 0];
% 目标位置
p_end = [0.5 0.3 0.2];
% 运动时间
t_start = 0;
t_end = 5;
t = linspace(t_start, t_end, 100);
% 直线插补
p = p_start + (p_end - p_start) * (t - t_start) / (t_end - t_start);

上述代码在笛卡尔坐标系中定义了起始位置pstart和目标位置pend，以及运动时间范围。通过简单的线性关系，根据时间向量t计算出每个时刻末端执行器在笛卡尔空间中的位置p，实现了直线插补的轨迹规划。

四、机器人工具箱建立的模型对比

机器人工具箱是MATLAB中专门用于机器人研究的工具包，它提供了便捷的函数来建立机器人模型。与我们自制的Simscape模型相比，机器人工具箱建立的模型在使用上可能更加简洁直观。

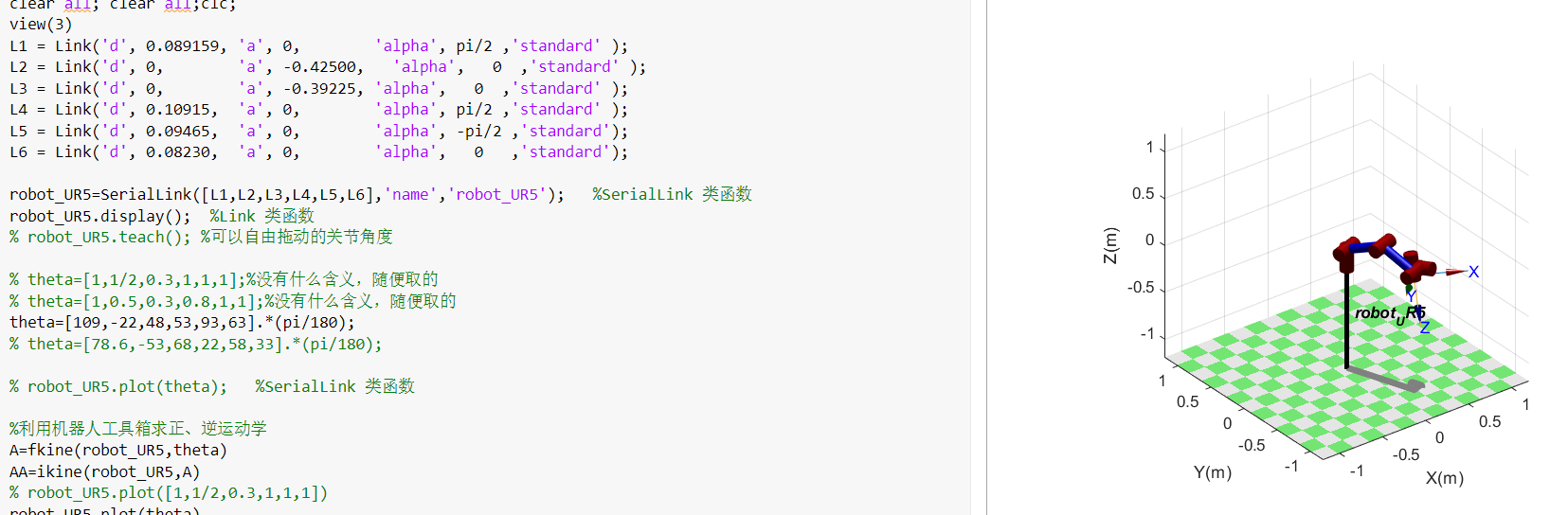
% 使用机器人工具箱建立UR5模型
L(1) = Link('d', 0.089159, 'a', 0, 'alpha', pi/2);
L(2) = Link('d', 0, 'a', -0.425, 'alpha', 0);
L(3) = Link('d', 0, 'a', -0.3922, 'alpha', 0);
L(4) = Link('d', 0.10915, 'a', 0, 'alpha', pi/2);
L(5) = Link('d', 0.09465, 'a', 0, 'alpha', -pi/2);
L(6) = Link('d', 0.0823, 'a', 0, 'alpha', 0);
ur5 = SerialLink(L, 'name', 'UR5');

上述代码使用机器人工具箱的Link函数定义了UR5机器人的各个连杆参数，然后通过SerialLink函数建立了UR5机器人模型ur5。通过对比可以发现，机器人工具箱建立模型的方式更侧重于参数化定义，而Simscape建模则更接近实际物理结构的搭建，两者各有优劣，在不同的研究场景下可以灵活选择使用。

通过以上对UR5机器人在MATLAB中的建模、运动学分析以及轨迹规划的探索，我们对机器人的运动控制有了更深入的理解。无论是自制建模还是使用机器人工具箱，MATLAB都为我们提供了强大的工具来研究和开发机器人相关的应用。希望这篇博文能给大家在机器人学习和研究中带来一些启发。