Python 高级：人工智能（线性回归、岭回归、逻辑回归）

1、机器学习算法怎么从数据中学习规律线性回归：，和称之为可训练参数；算法学习：找到最优的可训练参数；构造损失函数：。函数值越小，模型的预测值与真实值越接近，求最小的时候和的值。2、线性回归apifrom sklearn.linear_model import LinearRegression# 获取数据x = [[80, ...

马尔盖云

598人浏览 · 2019-12-16 16:19:24

马尔盖云 · 2019-12-16 16:19:24 发布

1. 机器学习算法怎么从数据中学习规律

线性回归： $h(\omega )=\omega_{1}x_{1}+\omega_{2}x_{2}+\cdots +\omega_{n}x_{n}$ ， $\omega$ 和 $b$ 称之为可训练参数；

算法学习：找到最优的可训练参数；

构造损失函数： $g=f(\omega ,b)$ 。函数值越小，模型的预测值与真实值越接近，求 $g$ 最小的时候 $\omega$ 和 $b$ 的值。

2. 线性回归api

from sklearn.linear_model import LinearRegression

# 获取数据
x = [[80, 86],
[82, 80],
[85, 78],
[90, 90],
[86, 82],
[82, 90],
[78, 80],
[92, 94]]
y = [84.2, 80.6, 80.1, 90, 83.2, 87.6, 79.4, 93.4]
# 机器学习
estimator = LinearRegression()
estimator.fit(x,y)
# 获取回归系数
estimator.coef_
# 获取偏置
estimator.intercept_

3. 波士顿房价预测

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import SGDRegressor

# 正规方程优化    
# 1、获取数据
data = load_boston()
# 2、数据基本处理 划分数据集
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2, random_state=10)
# 3、特征工程 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4、机器学习 正规方程
# 4.1 创建模型 实例化估计器
estimator = LinearRegression()
# 4.2 训练模型
estimator.fit(x_train, y_train)
# 5、模型评估 MSE 均方误差 预测值和真实值
# 5.1 获取预测值
y_predict = estimator.predict(x_test)
# 5.2 计算MSE
mean_squared_error(y_pred=y_predict, y_true=y_test)

# 梯度下降优化
# 1、获取数据
data = load_boston()
# 2、数据基本处理 划分数据集
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2, random_state=10)
# 3、特征工程 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4、机器学习 正规方程
# 4.1 创建模型 实例化估计器
estimator = SGDRegressor(max_iter=10000, tol=0.000001)
# 4.2 训练模型
estimator.fit(x_train, y_train)
# 5、模型评估 MSE 均方误差 预测值和真实值
# 5.1 获取预测值
y_predict = estimator.predict(x_test)
# 5.2 计算MSE
mean_squared_error(y_pred=y_predict, y_true=y_test)

4. 正则化

Ridge岭回归代价函数：

$J(\theta )=MSE(\theta )+\alpha \sum_{i+1}^{n}\theta _{i}^{2}$

Lasso岭回归代价函数：

$J(\theta )=MSE(\theta )+\alpha \sum_{i+1}^{n}|\theta _{i}|$

L2正则化：

使得其中一些w的值都很小，都接近于0，削弱某个特征的影响，Ridge回归。

L1正则化：

使得其中一些w的值直接为0，删除这个特征的影响，LASSO回归。

目标函数：

目标函数=损失函数+正则项

Ridge岭回归代码实现：

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import SGDRegressor
from sklearn.linear_model import Ridge

# 1、获取数据
data = load_boston()
# 2、数据基本处理 划分数据集
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2, random_state=10)
# 3、特征工程 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4、机器学习 正规方程
# 4.1 创建模型 实例化估计器
estimator = Ridge(alpha=1.0)
# 4.2 训练模型
estimator.fit(x_train, y_train)
# 5、模型评估 MSE 均方误差 预测值和真实值
# 5.1 获取预测值
y_predict = estimator.predict(x_test)
# 5.2 计算MSE
mean_squared_error(y_pred=y_predict, y_true=y_test)

5. 模型的保存和加载

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import SGDRegressor
from sklearn.linear_model import Ridge
from sklearn.externals import joblib

# 1、获取数据
data = load_boston()
# 2、数据基本处理 划分数据集
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2, random_state=10)
# 3、特征工程 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4、机器学习 正规方程
# 4.1 创建模型 实例化估计器
# estimator = Ridge(alpha=1.0)
# 4.2 训练模型
# estimator.fit(x_train, y_train)
# 保存模型
# joblib.dump(estimator, './1217.pkl')
# 加载模型
estimator=joblib.load('./1217.pkl')
# 5、模型评估 MSE 均方误差 预测值和真实值
# 5.1 获取预测值
y_predict = estimator.predict(x_test)
# 5.2 计算MSE
mean_squared_error(y_pred=y_predict, y_true=y_test)

6. 逻辑回归

线性回归输入：

$h(\omega )=\omega_{1}x_{1}+\omega_{2}x_{2}+\cdots +\omega_{n}x_{n}$

sigmoid激活函数：

$S(x)=\frac{1}{1+e^{-x}}$

线性回归的结果输入到sigmoid函数当中，输出结果为[0, 1]区间中的一个概率值，默认为0.5为阈值

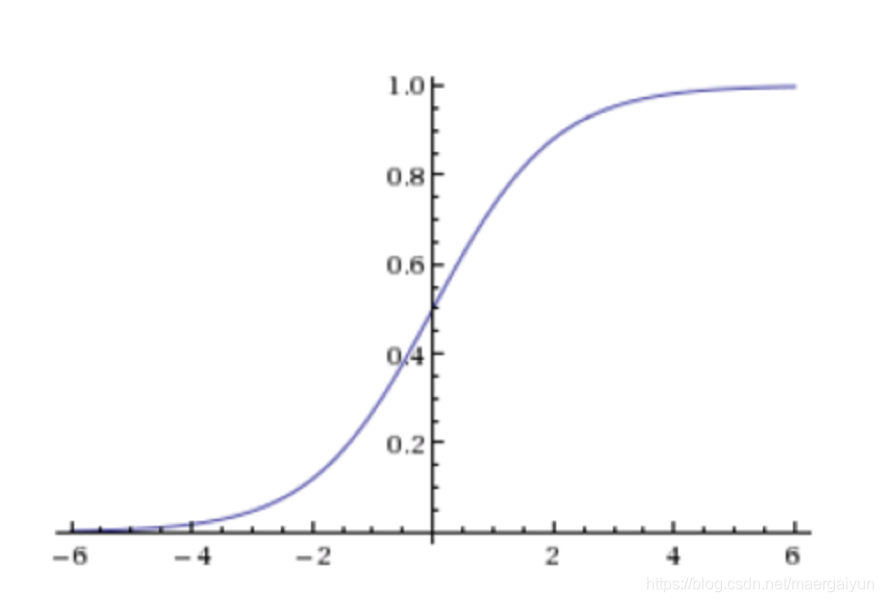
对数似然损失：

$cost(h_{\theta}(x),y)=\sum_{i=1}^{m}-y_{i}log(h_{\theta }(x))-(1-y_{i})log(1-h_{\theta}(x))$

7. 癌症分类预测

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression

# 1.获取数据 在线下载
names = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape',
                   'Marginal Adhesion', 'Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin',
                   'Normal Nucleoli', 'Mitoses', 'Class']
data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data",
                  names=names)
# 2.数据基本处理 
# 缺失值处理('?'标记)
data = data.replace(to_replace='?', value=np.NaN)
data = data.dropna()
# 划分数据集
x = data.iloc[:, 1:10] # 特征值
y = data['Class']
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
# 3.特征工程 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4.机器学习 逻辑回归建模
# 4.1 建立模型
estimator = LogisticRegression()
# 4.2 训练模型
estimator.fit(x_train, y_train)
# 5.模型评估
estimator.score(x_test, y_test)

# 分类评估报告
# 获取预测值
y_predict = estimator.predict(x_test)
# 获取分类评估报告
res = classification_report(y_true=y_test, y_pred=y_predict, labels=[2,4], target_names=['良性', '恶性'])
print(res)