数据结构——栈（C语言：超详细）

栈，一种后进先出的线性数据结构，虽简单却至关重要。它如程序运行的基石，管理函数调用、实现递归，还高效解决括号匹配、表达式求值等问题。栈简化复杂操作，广泛应用于操作系统、编译器等，是计算机科学不可或缺的强大工具，理解它对于掌握编程至关重要。效率，解决复杂问题，是算法的基础，也是程序设计中不可或缺的关键要素。

Windfall＼(`Δ’)／

2807人浏览 · 2025-01-12 22:38:55

Windfall＼(`Δ’)／ · 2025-01-12 22:38:55 发布

hello！这里是敲代码的小董，很荣幸您阅读此文，期待您的评论指点和关注，欢迎欢迎~~

✨✨个人主页：敲代码的小董

💗💗系列专栏：数据结构

一、引言

1. 我们为什么要学习栈？

1.1 栈的重要性

栈，一种后进先出的线性数据结构，虽简单却至关重要。它如程序运行的基石，管理函数调用、实现递归，还高效解决括号匹配、表达式求值等问题。栈简化复杂操作，广泛应用于操作系统、编译器等，是计算机科学不可或缺的强大工具，理解它对于掌握编程至关重要。

1.2 栈在实际应用中的场景举例

浏览器的后退按钮:

场景: 点击浏览器上的后退按钮返回上一个页面。

栈的应用: 浏览器用一个栈来存储你访问过的网页，每次访问新页面就压入栈，点击后退就从栈顶弹出页面。

说明: 栈的后进先出特性完美对应后退操作。

文本编辑器的撤销操作:

场景: 在编辑器中进行编辑后，按下撤销按钮回到之前的状态。

栈的应用: 编辑器使用一个栈来记录你的编辑操作，每次编辑压入栈，撤销时弹出栈顶的操作并还原。

说明: 栈按时间顺序记录操作，方便撤销。

程序中的函数调用:

场景: 当一个函数调用另一个函数时。

栈的应用: 计算机使用调用栈来管理函数调用，每次调用函数就压入当前函数的运行状态，函数结束就弹出。

说明: 栈保证了函数调用顺序正确和局部变量的隔离。

2. 数据结构概述

1. 简单回顾数据结构的概念

数据结构是计算机中组织和存储数据的方式，它不仅定义了数据的逻辑关系，还包括数据在计算机内存中的实际存储方式，以及针对这些数据可以执行的操作。选择合适的数据结构能够提高程序效率，解决复杂问题，是算法的基础，也是程序设计中不可或缺的关键要素。

数据结构：是相互之间存在一种或多种特定关系的数据元素的集合。

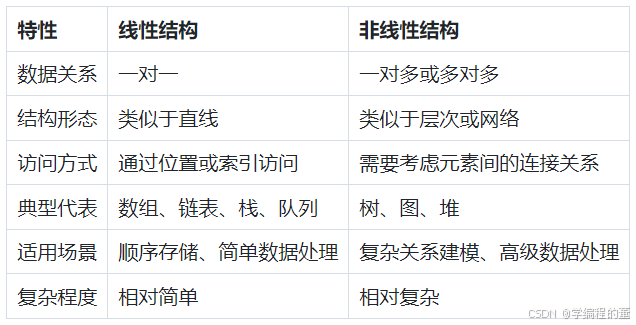
2. 线性结构和非线性结构

线性结构 (Linear Structure)

定义：线性结构是指数据元素之间存在一对一的线性关系

特点：
①数据元素排列成一条直线，就像一根绳子上串着珠子。

②元素之间存在顺序关系，可以通过位置或索引访问元素。

③常见的操作包括插入、删除、查找、遍历等。

举例：数组、链表、栈、队列。

非线性结构 (Non-linear Structure)

定义：非线性结构是指数据元素之间存在一对多或多对多的关系

特点：
①数据元素之间的关系不是简单的线性顺序，而是复杂的层次或网络关系。

②访问元素的方式比线性结构复杂，需要考虑不同元素之间的连接关系。

③常见的操作包括遍历、搜索、插入、删除等。

举例：树、图、堆

那么栈是什么呢？？？

二、栈的基本概念

1. 什么是栈？

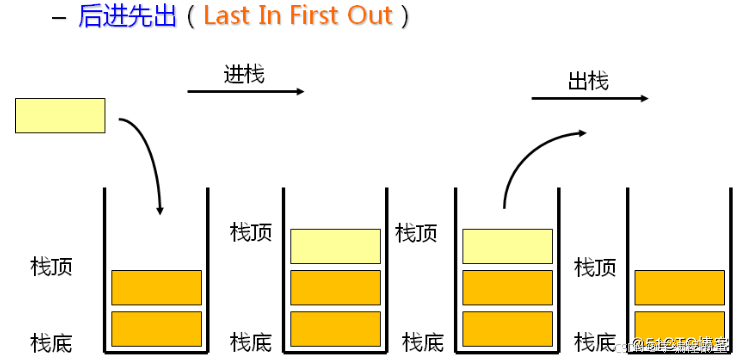
栈是一种特殊的线性数据结构，它遵循 后进先出（Last-In, First-Out，LIFO） 的原则。形象地理解，栈就像一个只有一个开口的桶，我们只能从桶的顶部放入（push）或取出（pop）元素。

1.1 生活中的栈

例如：枪械中的子弹夹。

入栈 (Push)： 将子弹装入弹夹，从弹夹顶部放入。

出栈 (Pop)： 从弹夹顶部取出子弹进行射击。

栈顶 (Top)： 弹夹最顶部的子弹。

后进先出 (LIFO)： 最后装入的子弹会最先被射出。

2. 栈的基本操作

栈的基本操作主要包括以下几种，它们构成了栈的核心功能，并遵循后进先出（LIFO）的原则：

2.1 入栈（Push）

定义： 入栈操作是将一个新元素添加到栈顶的过程。

过程：

首先，确定栈是否已满（如果使用固定大小的数组实现），如果栈已满，则无法入栈，通常会抛出“栈溢出”错误。

如果栈未满，则将新元素放置在当前栈顶的上方，成为新的栈顶元素。

栈顶指针（通常用一个变量表示）向上移动，指向新的栈顶元素。

示例：如果栈中已有元素 [1, 2, 3]，执行 push(4) 后，栈变为 [1, 2, 3, 4]。

形象比喻： 就像往一个弹夹里面压入一个新的子弹。

2.2 出栈（Pop）

定义： 出栈操作是从栈顶移除一个元素的过程。

过程：

首先，确定栈是否为空。如果栈为空，则无法出栈，通常会抛出“栈为空”错误。

如果栈不为空，则先取出栈顶元素。

栈顶指针向下移动，指向新的栈顶元素（或栈空状态）。

示例：如果栈中已有元素 [1, 2, 3, 4]，执行 pop() 后，栈变为 [1, 2, 3]，并返回元素 4。

形象比喻： 从弹夹顶部取出一个子弹进行射击。

2.3 查看栈顶（Peek / Top）

定义： 查看栈顶操作是获取栈顶元素的值，但并不移除该元素。

过程：

首先，确定栈是否为空。如果栈为空，则无法查看栈顶，通常会返回一个特定值（例如：null）或抛出错误。

如果栈不为空，则返回栈顶元素的值。

栈本身不发生变化，栈顶指针位置不变。

示例：如果栈中已有元素 [1, 2, 3, 4]，执行 peek() 或 top() 后，返回元素 4，栈仍然是 [1, 2, 3, 4]。

形象比喻： 就像看一眼一个弹夹最上面那个子弹，但是不把它拿走。

2.4 判空（isEmpty）

定义： 判空操作是判断栈是否为空的过程。

过程：

检查栈中是否还有元素。

如果栈中没有任何元素，则返回 true；否则，返回 false。

示例：

如果栈为空，执行 isEmpty() 后，返回 true。

如果栈中有元素 [1, 2, 3]，执行 isEmpty() 后，返回 false。

2.5 获取栈的大小（Size）

定义： 获取栈的大小操作是返回栈中当前元素的数量。

过程：

返回栈中元素的个数。

示例：

如果栈为空，执行 size() 后，返回 0。

如果栈中有元素 [1, 2, 3]，执行 size() 后，返回 3。

2.6 总结

这五个基本操作是定义栈这种数据结构的关键。它们保证了栈的后进先出的特性，使得栈可以有效地解决许多特定类型的问题。掌握这些操作，是理解和使用栈的基础。

在实际编程中，可以使用不同的方式来实现栈，例如，可以使用数组或链表来实现。无论使用哪种方式，都需要正确地实现这些基本操作。

三、栈的实现方式

1. 基于数组实现栈

1.1 定义栈结构

1.1.1 静态栈

#define N 10
struct Stack
{
	int a[N];
	int top;
};

静态栈最大的缺点在于其固定大小的限制，这使得它在灵活性、内存利用率和处理能力方面都存在不足。在实际编程中，如果需要栈的容量动态增长或者需要处理复杂数据场景，通常需要使用动态栈（基于动态内存分配）或者其他更适合的数据结构。

1.1.2 动态栈

动态栈解决了固定大小栈的限制，可以根据实际需要动态调整栈的大小。在实际应用中，需要权衡动态栈的灵活性和扩容的开销，选择合适的栈实现方式。在基于数组实现栈，这里我们使用动态栈进行。

// 定义栈的数据类型
typedef int STDataType; //使用 typedef 将 int 类型重命名为 STDataType
                        //这样做的目的是为了方便将来修改栈中存储的数据类型，
                        //例如，如果想存储 float 类型，只需要修改 typedef 这一行即可。

// 定义栈的结构体
typedef struct Stack
{
    STDataType* a;      //a是一个指向 STDataType 类型的指针，用于动态存储栈中的元素
    int top;            //top是栈顶的下一个位置
    int capacity;       //capacity 是一个整型变量，用于表示栈的当前容量
} ST;

1.2 初始化

void STInit(ST* ps)
{
	assert(ps);                    
	ps->a = (STDataType*)malloc(sizeof(STDataType) * 4);
	if (ps->a==NULL)
	{
		perror("malloc fail");
		return;
	}
	ps->capacity = 4;           //设置栈的初始容量为 4
	ps->top = 0;	            //top是栈顶的下一个位置
}

1.3 入栈

void STPush(ST* ps, STDataType x)
{
	assert(ps);                         //断言，确保栈指针 ps 不为空
    //判断栈是否已满
	if (ps->top==ps->capacity)
	{
        //扩容
		STDataType* tmp= (STDataType*)realloc(ps->a, sizeof(STDataType) * ps->capacity * 2);
        //判断扩容是否成功
		if (tmp==NULL)
		{
			perror("realloc fail");
			return; //扩容失败，返回
		}
        //更新栈的数组指针和容量
		ps->a = tmp;
		ps->capacity = ps->capacity * 2;
		tmp = NULL;
	}
	ps->a[ps->top] = x;                //将元素 x 放入栈顶
	ps->top++;                         //栈顶指针 top 加 1，指向下一个可用的位置
}

1.4 出栈

只有栈中有元素时，才可以出栈。

void STPop(ST* ps)
{
	assert(ps);
	assert(!STEmpty(ps));
	ps->top--;
}

1.5 查看栈顶元素

STDataType STTop(ST* ps)
{
	assert(ps);
	assert(!STEmpty(ps));
	return ps->a[ps->top - 1];

1.6 判断栈是否为空

bool STEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}

1.7 获取栈的大小

int STSize(ST* ps)
{
	assert(ps);
	return ps->top;
}

1.8 销毁栈

void STDestory(ST* ps)
{
	assert(ps);
	free(ps->a);                //释放栈数组 a 的内存  
	ps->a = NULL;               //将栈数组指针 a 置为 NULL
	ps->top = 0;                //将栈顶指针 top 置为 0
	ps->capacity = 0;           //将栈的容量 capacity 置为 0 
}

2. 基于链表实现栈

链表实现栈的核心思想是利用链表节点的动态分配和连接特性。栈的“后进先出”原则通过链表的头插和头删操作来实现。栈顶指针始终指向链表的第一个节点，即栈顶元素。入栈时，创建一个新节点，将其插入链表头部，并更新栈顶指针。出栈时，移除链表头部节点，并更新栈顶指针，释放移除节点的内存。由于链表的动态特性，栈的大小可以灵活调整，避免了固定容量的限制。

2.1 定义栈结构

单链表的类型定义

typedef struct ListNode 
{
    LTDataType data;        //数据域
    struct ListNode* next;  //指向下一个节点的指针
} ListNode;

栈结构体定义

typedef struct Stack 
{
    ListNode* top;    //指向栈顶节点的指针
} ST;

2.2 初始化

void STInit(ST* ps) 
{
    assert(ps);
    ps->top = NULL;
}

2.3 入栈

void STPush(ST* ps, LTDataType x) 
{
    assert(ps);
    ListNode* newNode = (ListNode*)malloc(sizeof(ListNode));
    if (newNode == NULL) 
    {
        perror("malloc fail");
        return;
    }
    newNode->data = x;
    newNode->next = ps->top;
    ps->top = newNode;
}

2.4 出栈

void STPop(ST* ps) 
{
    assert(ps);
    assert(!STEmpty(ps));
    ListNode* topNode = ps->top;
    ps->top = topNode->next;
    free(topNode);
}

2.5 查看栈顶元素

LTDataType STTop(ST* ps) 
{
    assert(ps);
    assert(!STEmpty(ps));
    return ps->top->data;
}

2.6 判断栈是否为空

bool STEmpty(ST* ps) 
{
    assert(ps);
    return ps->top == NULL;
}

2.7 获取栈的大小

int STSize(ST* ps) 
{
    assert(ps);
    int size = 0;
    ListNode* cur = ps->top;
    while (cur) 
    {
        size++;
        cur = cur->next;
    }
    return size;
}

2.8 销毁栈

void STDestory(ST* ps) 
{
    assert(ps);
    ListNode* cur = ps->top;
    while (cur) 
    {
        ListNode* next = cur->next;
        free(cur);
        cur = next;
    }
    ps->top = NULL;
}

链表实现栈的优缺点
优点：动态扩容，灵活
缺点：需要额外的指针空间

四、课后习题

利用栈进行括号匹配的原理，完成括号匹配问题。

typedef char STDataType;
typedef struct Stack
{
	STDataType *a;
	int top;
	int capacity;
}ST;

void STInit(ST* ps);
void STDestory(ST* ps);

void STPush(ST* ps, STDataType x);
void STPop(ST* ps);
int STSize(ST* ps);
bool STEmpty(ST* ps);
STDataType STTop(ST* ps);
void STInit(ST* ps)
{
	assert(ps);
	ps->a = (STDataType*)malloc(sizeof(STDataType) * 4);
	if (ps->a==NULL)
	{
		perror("malloc fail");
		return;
	}
	ps->capacity = 4;
	ps->top = 0;	//top是栈顶的下一个位置
	//ps->top = -1;	//top是栈顶元素位置
}

void STDestory(ST* ps)
{
	assert(ps);

	free(ps->a);
	ps->a = NULL;
	ps->top = 0;
	ps->capacity = 0;
}
void STPush(ST* ps, STDataType x)
{
	assert(ps);
	if (ps->top==ps->capacity)
	{
		STDataType* tmp= (STDataType*)realloc(ps->a, sizeof(STDataType) * ps->capacity * 2);
		if (tmp==NULL)
		{
			perror("realloc fail");
			return;
		}
		ps->a = tmp;
		ps->capacity = ps->capacity * 2;
		tmp = NULL;
	}
	ps->a[ps->top] = x;
	ps->top++;
}
void STPop(ST* ps)
{
	assert(ps);
	assert(!STEmpty(ps));
	ps->top--;
	
}
int STSize(ST* ps)
{
	assert(ps);
	return ps->top;
}
bool STEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}
STDataType STTop(ST* ps)
{
	assert(ps);
	assert(!STEmpty(ps));
	return ps->a[ps->top - 1];
}
bool isValid(char* s) 
{
    ST st;
    STInit(&st);
    while(*s)
    {
        if(*s=='('||*s=='['||*s=='{')
        {
            STPush(&st,*s);
        }
        else
        {
            if(STEmpty(&st))
            {
                STDestory(&st);
                return false;
            }
            char top =STTop(&st);           //拿数据
            STPop(&st);                     //弹出栈顶元素

            if((*s==')'&&top!='(')
             ||(*s==']'&&top!='[')
             ||(*s=='}'&&top!='{'))
            {
                STDestory(&st);             //不销毁会导致内存泄漏
                return false;
            }
        }
        ++s;
    }
    bool ret=STEmpty(&st);
    
    STDestory(&st);
    return ret;
}

DAMO开发者矩阵

DAMO开发者矩阵，由阿里巴巴达摩院和中国互联网协会联合发起，致力于探讨最前沿的技术趋势与应用成果，搭建高质量的交流与分享平台，推动技术创新与产业应用链接，围绕“人工智能与新型计算”构建开放共享的开发者生态。

更多推荐

协作机器人的运动学逆解数值解法介绍

摘要：针对协作机器人逆运动学求解问题，本文分析了数值解法的适用场景（非球形腕、冗余结构等），建立了误差函数模型，并比较了牛顿法、阻尼最小二乘法(DLS)和投影梯度法三种主流数值解法。重点阐述了DLS算法的实现流程与关键细节，包括误差度量、雅可比计算和收敛判据等。针对协作机器人特点，提出了关节限位处理、避障集成等增强策略。通过对比表指出DLS是7轴协作机器人的首选方法，推荐采用自适应DLS结合零空间