计算二叉树的高度：

二叉树的高度，其实就是计算二叉树的层数

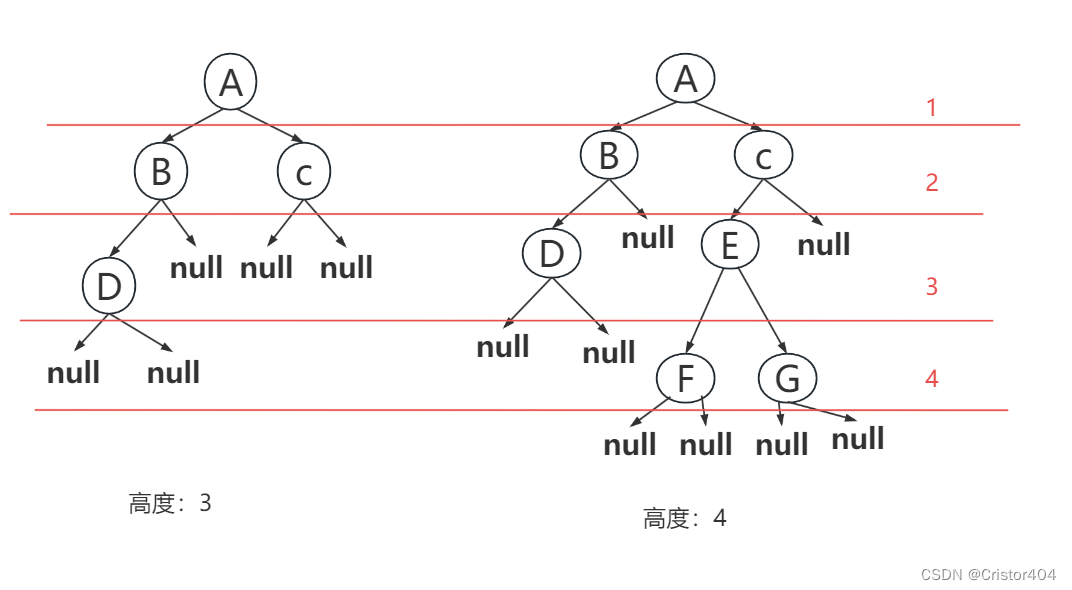
 可以使用层序遍历的思想，逐层增加，每增加一层，高度就加+1，这样就可以实现二叉树高度的计算：

大致执行步骤图解: 

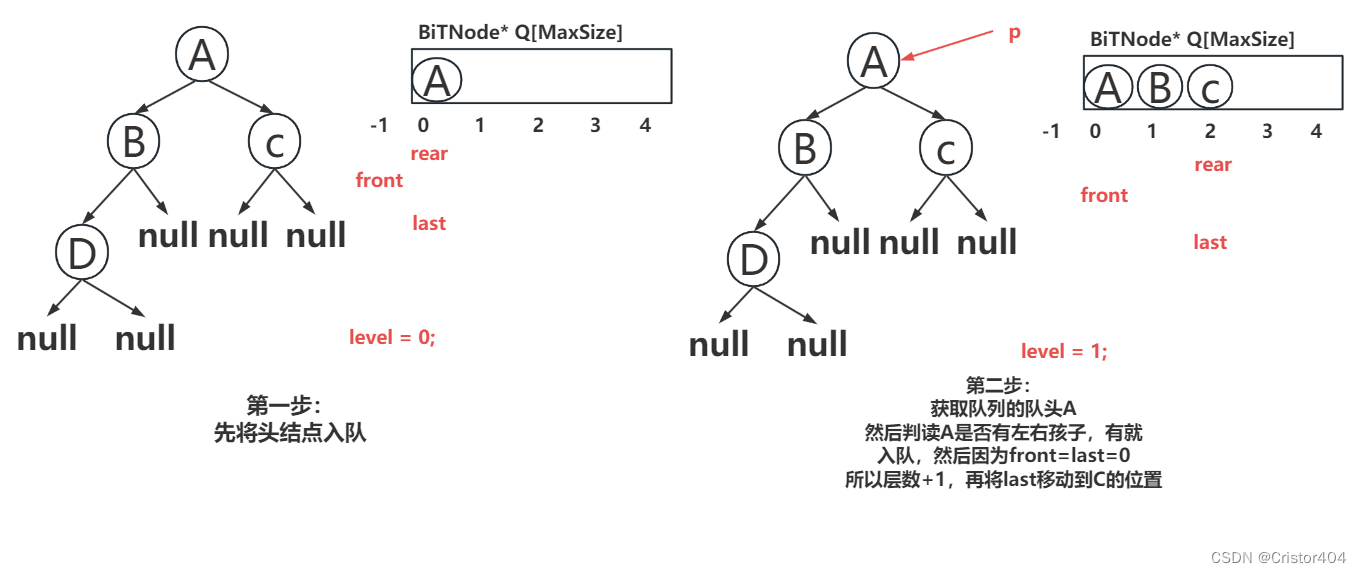
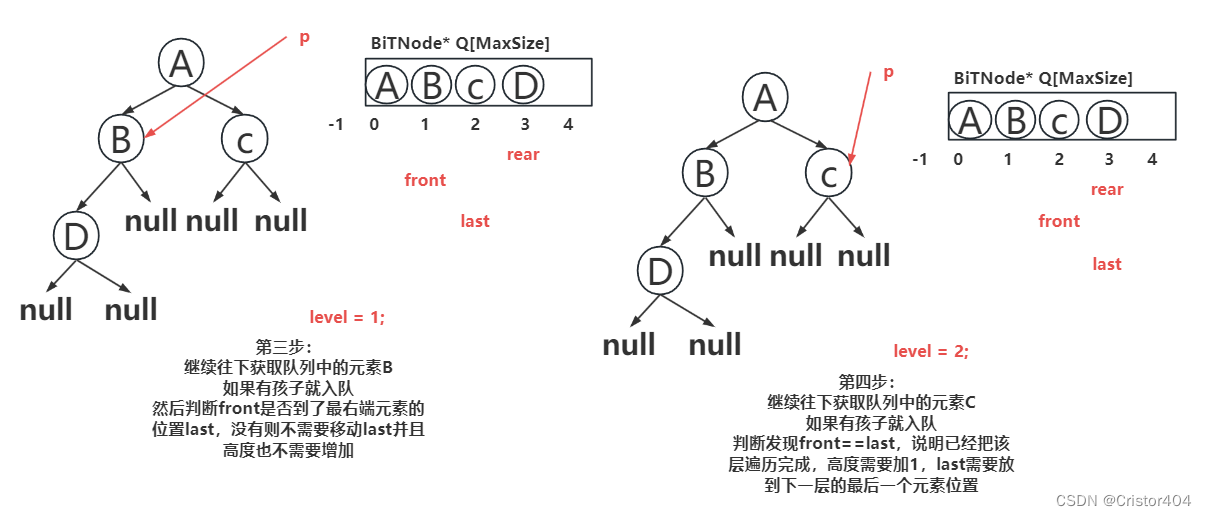
非递归版代码部分:

int BtdepTh(BiTree T){
	if(!T){
		return 0;    //若此数为空 则高度为0
	}
	int front = -1,rear = -1;    //front用于记录当前访问的结点，rear用于记录最后一个元素
	int last = 0,level = 0;      //last用于遍历时记录每一层的最右端元素在数组中的位置
	BiTNode* p;                  //level为树的层数 也是高度
	BiTNode* Q[MaxSize];         //用于存放层序遍历的结点序列
	Q[++rear] = T;               //先将根结点加入数组
	while(front<rear){
		p = Q[++front];          //依次获取层序队列中的元素
		if(p->lchild)            //有左孩子就加入到层序遍历的序列
			Q[++rear] = p->lchild;
		if(p->rchild)            //有右孩子也加入到层序遍历的序列
			Q[++rear] = p->rchild;
		if(front==last){         //当遍历结点下标front刚好遍历到当前层的最右端元素时
			level++;             //层数增加 将last设置成下一层的最右端元素在序列中的位置
			last = rear;
		}
	}
	return level;
}

递归版代码部分：

int Btdepth2(BiTree T){
	if(T==NULL)    //走到叶子结点的孩子时 直接返回0
		return 0;
	int ldep = Btdepth2(T->lchild);    //往左走
	int rdep = Btdepth2(T->rchild);    //往右走
	if(ldep>rdep)                      //判断左边和右边哪个高度更高并且返回最大值
		return ldep+1;
	else
	 	return rdep+1;
}

计算二叉树的宽度：

二叉树的宽度其实就是指拥有最多结点数的层数的结点数

如果哪一层拥有的结点数最多，那么二叉树的宽度就是该层的结点数 

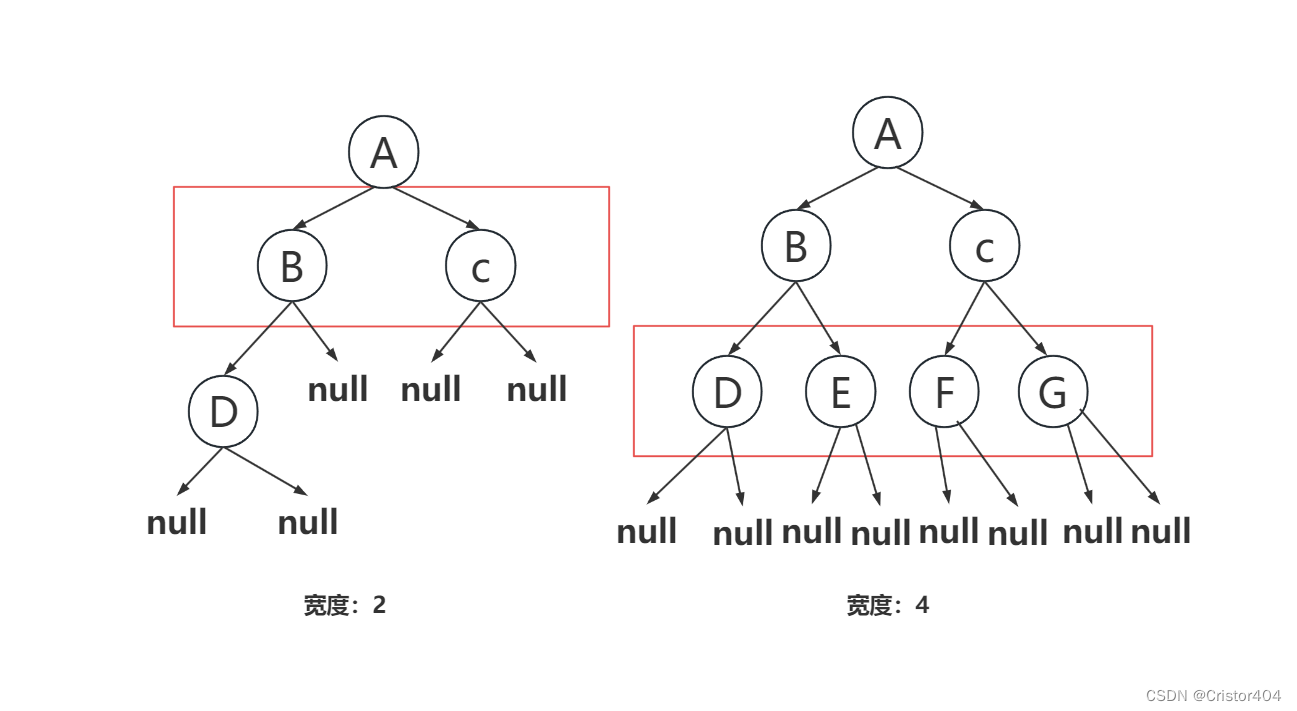
大概执行步骤如下图：

循环1：

这一步主要是为了先将每一层的孩子初始化，采用层序遍历的思想将孩子入队，并且设置他们对应的高度(所在层次)。

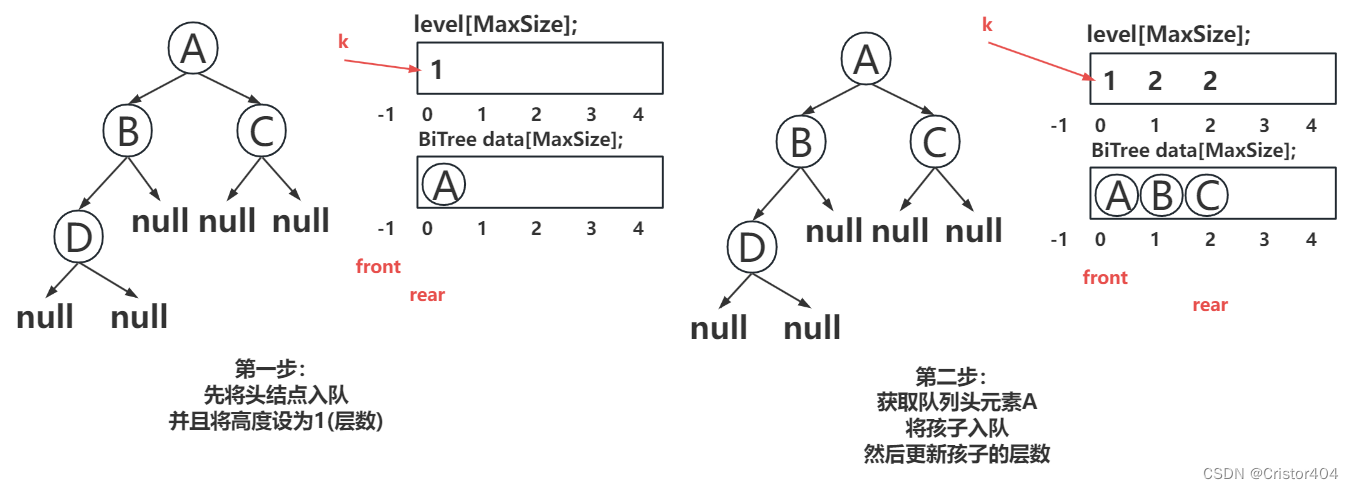
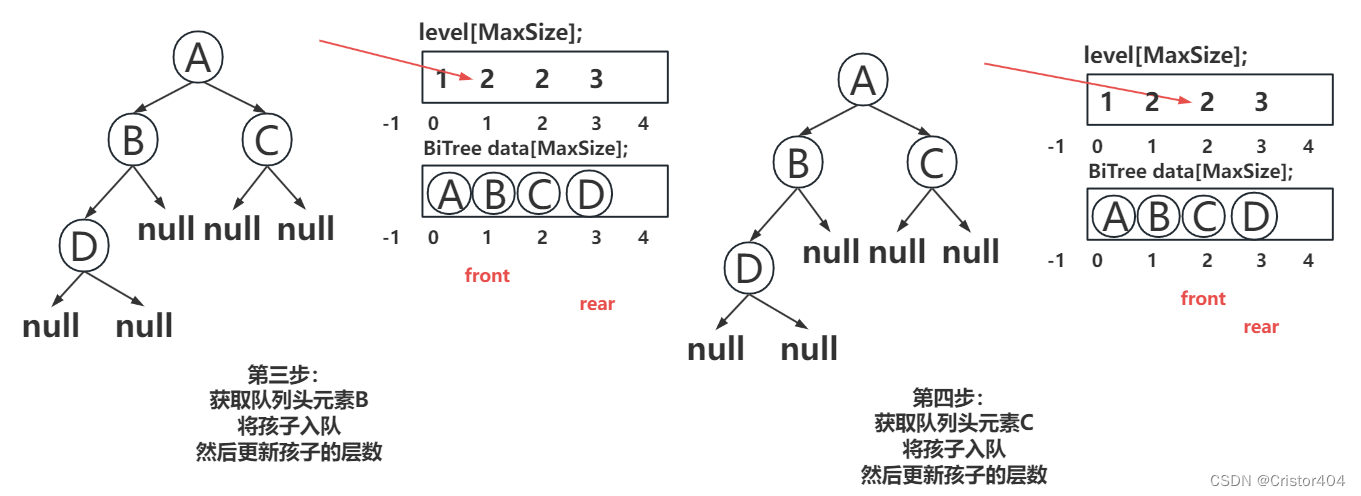
循环2：

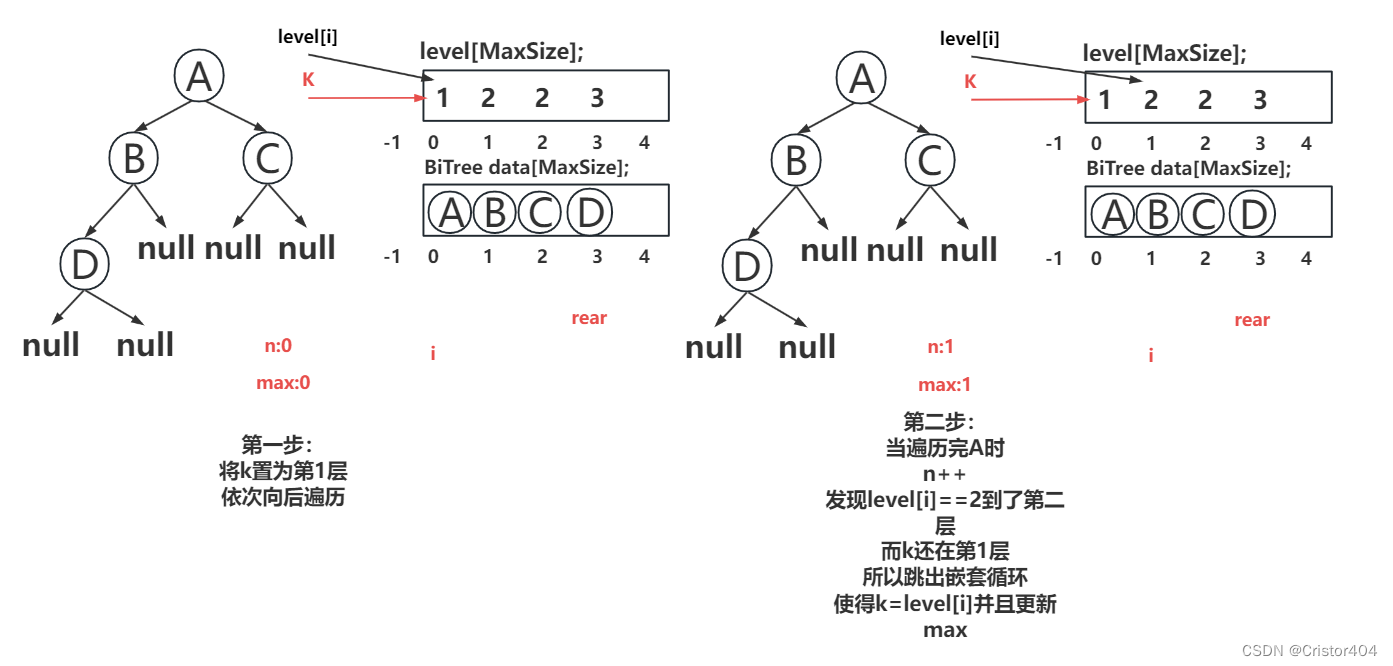
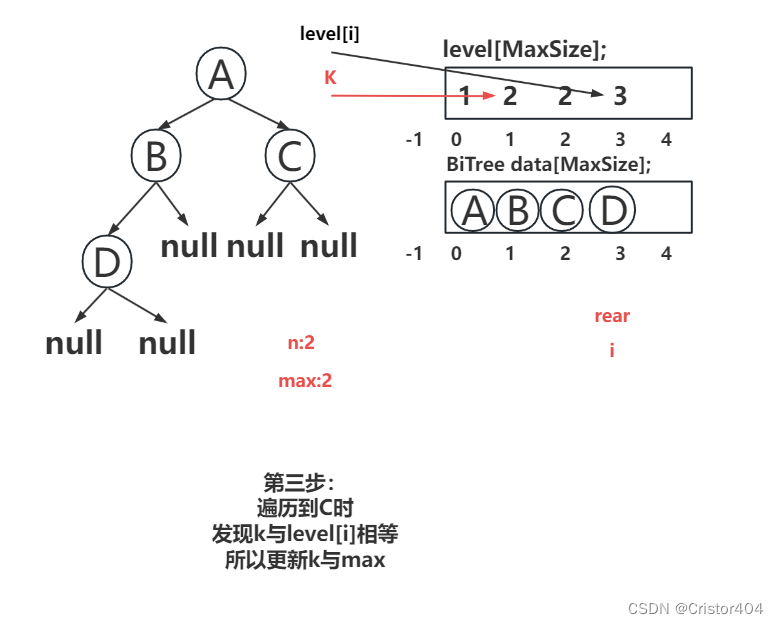
代码部分:

typedef struct{
	BiTree data[MaxSize];    //存储结点的队列
	int level[MaxSize];      //存储结点所在的层数
	int front,rear;          //front表示当前遍历的结点下标
}Qus;                        //rear表示入队的结点的下标

int BtWeith(BiTree T){
	Qus Qu;                    
	BiTree p;int k,max,i,n;  //k用于存放当前层数,max存放最大宽度
	Qu.front = Qu.rear = -1; //先将front与rear下标设置为-1 因为队列下标0为开始位置
	Qu.rear++;               //将rear置于队头位置0
	Qu.data[Qu.rear]=T;      //根节点入队
	Qu.level[Qu.rear] = 1;   //根结点入队 就说明已经有一层 第一层一定只能有一个结点
	while(Qu.front<Qu.rear){
		Qu.front++;            
		p = Qu.data[Qu.front];    //获取队头结点
		k = Qu.level[Qu.front];   //获取当前结点所在层数
		if(p->lchild!=NULL){      //若有孩子就入队
			Qu.rear++;
			Qu.data[Qu.rear] = p->lchild;
			Qu.level[Qu.rear] = k+1;    //有孩子，说明还有下一层，高度加1
		}
		if(p->rchild!=NULL){
			Qu.rear++;
			Qu.data[Qu.rear] = p->rchild;
			Qu.level[Qu.rear] = k+1;
		}
	}
    //获取最大宽度的部分
	max = 0;i = 0;
	k = 1;  //从第一层开始遍历
	while(i<=Qu.rear){    //依次遍历所有结点
		n = 0;        
		while(i<=Qu.rear&&Qu.level[i]==k){    //遍历每一层
			n++;    //该层宽度增加
			i++;
		}
		k=Qu.level[i];  //获取下一层层数
		if(n>max) max = n;    //如果有更大的宽度 就将max设置为最大的宽度
	}
	return max;
}