(图像配准)TPS薄板样条变换计算原理
我们重新假设已经获取到两张图像的n组匹配点对:(P1(x1,y1),P1’(x1’,y1’))、P2((x2,y2),P2’(x2’,y2’))、…上式中只要求出 a1,a2,a3和wi(1≤i≤n),就可以确定f(x,y),其中U是基函数,在样条函数中的前三项是仿射变换部分(负责整体的平移、缩放、旋转等线性操作),后面一项是对局部形变的描述。由上述可见r为欧氏距离,(xi,yi)是空间中任意一个
TPS(Thin Plate Spline,薄板样条)是一种非刚性形变,一种插值方法,该方法的输入是两张图像中的多组匹配点对,常见的获取匹配点对算法为SIFT、SURF、ORB,以及光流跟踪等。 TPS的基本思想是让这些匹配点精确对齐,其他地方的自动、平滑的‘弯曲’过渡,同时‘弯曲能量’最小。
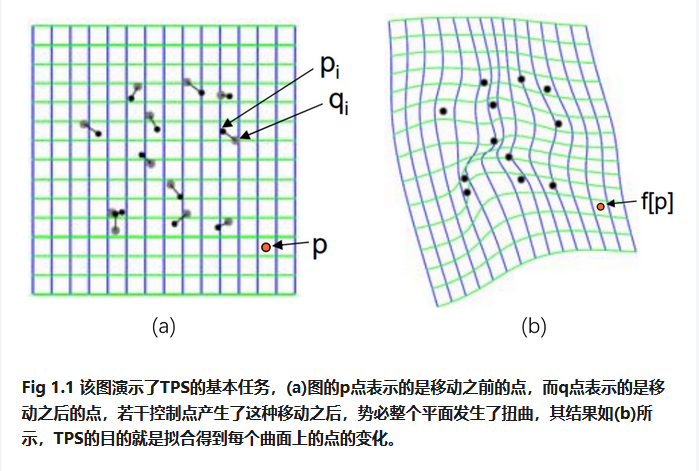
我们重新假设已经获取到两张图像的n组匹配点对:(P1(x1,y1),P1’(x1’,y1’))、P2((x2,y2),P2’(x2’,y2’))、…、(Pn(xn,yn), Pn’(xn’,yn’))。P1为变换前的点,P1’为变换后的点。TPS形变的目标是求解一个函数f,使得f(Pi)=Pi’ (1≤i≤n),并且弯曲能量函数最小,同时图像上的其它点也可以通过插值得到很好的校正。那么使用TPS变换计算图A与图B的坐标对应关系的过程如下。
样条函数形式:

上式中只要求出 a1,a2,a3和wi(1≤i≤n),就可以确定f(x,y),其中U是基函数,在样条函数中的前三项是仿射变换部分(负责整体的平移、缩放、旋转等线性操作),后面一项是对局部形变的描述。
基函数U的形式:
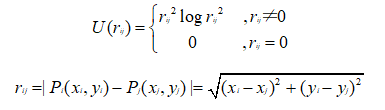
由上述可见r为欧氏距离,(xi,yi)是空间中任意一个待变形的点,控制点(xj,yj)也是事先规定变形目标的点(是一开始输入的图A图B的匹配点对,也就是控制点对)
记矩阵K、L、Y为:
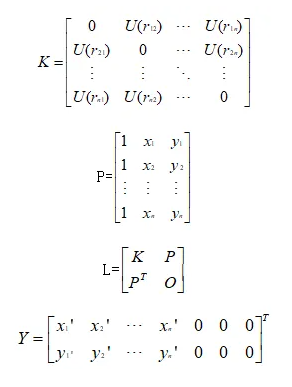
K:记录着控制点与待形变点的距离(决定着点与点之间形变程度),弯曲约束。
P:提供控制点的位置信息,用来算整体挪动旋转,仿射约束。
L :组合K、P,其中包含了如何弯曲、移动旋转。
Y:上半部分说明控制点需要被移动到的新位置的坐标数据,下半部分全0是用于仿射部分的约束条件(确保权重w的加权和为0)。
由LW=Y解得W矩阵:
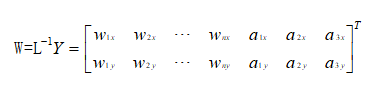
权重w:是n*1的列向量,n为控制点个数
仿射参数a:是TPS插值函数中的前三项的系数,a1:常数项(控制平移)、a2:x方向的线性系数、a3:y方向的线性系数。
从而有A的任意坐标(xi,yi)到B的任意坐标(xi’,yi’)的映射:
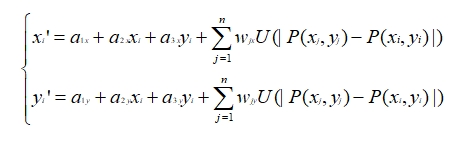

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容






所有评论(0)