欧拉角是描述三维空间中刚体方向的一组角度参数，通过绕不同坐标轴的旋转来表示物体的方位。它以数学家莱昂哈德·欧拉的名字命名，在机器人学、航空航天、计算机图形学等领域有广泛应用。以下是关于欧拉角的详细解析：

一、基本定义与旋转顺序

欧拉角通过三次绕坐标轴的旋转来确定刚体的方向，每次旋转围绕一个固定轴（或当前刚体的轴）进行。根据旋转轴的顺序不同，欧拉角有多种定义方式，常见的包括：

1. 经典欧拉角（Z-X-Z顺序）

分三步旋转：

- 绕世界坐标系的Z轴旋转角度α（偏航，Yaw）；

- 绕新的X轴旋转角度β（俯仰，Pitch）；

- 绕新的Z轴旋转角度γ（滚转，Roll）。

2. Tait-Bryan角（Z-Y-X顺序，也称为“导航欧拉角”）

航空航天中常用，对应：

- 绕Z轴旋转α（偏航）；

- 绕Y轴旋转β（俯仰）；

- 绕X轴旋转γ（滚转）。

注意：旋转顺序至关重要，不同顺序会导致不同的最终姿态（例如ZYX、YXZ等顺序均存在），使用时需明确约定。

二、数学表达与旋转矩阵

以Tait-Bryan角（Z-Y-X顺序）为例，三次旋转可分别用矩阵表示，最终旋转矩阵为三次旋转的乘积：

1. 绕Z轴旋转α

2. 绕Y轴旋转β

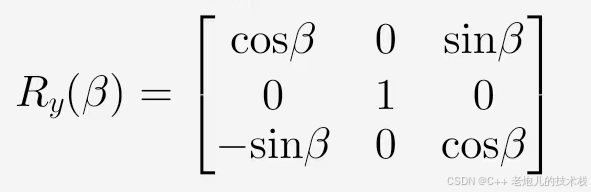
3. 绕X轴旋转γ

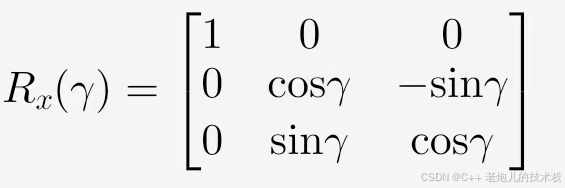
最终旋转矩阵：

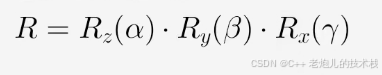
三、应用场景

- 航空航天：描述飞行器的偏航（Yaw，航向变化）、俯仰（Pitch，抬头/低头）、滚转（Roll，机翼倾斜）。

- 机器人学：表示机械臂末端执行器的姿态，或移动机器人的朝向。

- 计算机图形学：控制3D模型的旋转，直观实现用户交互操作。

- 运动捕捉：分析人体关节的旋转角度（如髋关节、肩关节等）。

四、优缺点

- 优点：

1. 直观易懂，符合人类对旋转的直觉（如“先转多少度，再转多少度”）。

2. 仅用三个参数即可表示三维姿态，参数少、计算简洁。

- 缺点：

1. 万向锁（Gimbal Lock）问题：当两次旋转轴重合时，会丢失一个自由度。例如，Tait-Bryan角中当俯仰角β=±90°时，偏航角α和滚转角γ的旋转轴会重合（如图1所示），导致无法区分两者的贡献，出现解不唯一的情况。

2. 角度插值不连续：直接对欧拉角做线性插值会导致旋转路径不光滑，需通过四元数等方法优化。

五、万向锁的示例与本质

以Tait-Bryan角为例，当俯仰角β=90°时：

- 原偏航角α绕Z轴旋转，滚转角γ绕X轴旋转；

- 当β=90°时，第一次旋转后的X轴与原Z轴重合，此时α和γ的旋转轴均为同一方向，导致“航向”和“滚转”的控制耦合，无法独立调整。

六、替代方案

- 四元数（Quaternion）：用四个参数表示旋转，无万向锁问题，插值平滑，广泛用于计算机图形学和机器人控制。

- 旋转矩阵（Rotation Matrix）：用3×3矩阵表示旋转，无万向锁，但需9个参数，存储和计算成本较高。

总结

欧拉角是描述三维旋转的基础工具，其直观性使其在工程中被广泛使用，但万向锁问题限制了其在高精度连续控制场景中的应用。实际应用中，常根据需求结合四元数或旋转矩阵来弥补欧拉角的不足。理解欧拉角的旋转顺序和万向锁机制，是掌握三维姿态表示的关键。