Python数学建模——多元线性回归模型（基于公式构建并拟合模型）

一、基础知识加实现

1.多元线性回归模型的作用

主要用于探索性（分析快速识别关键变量），以及预测建模（提供基线预测结果）。

2.代码实现(内含大量注释)：

#程序文件ex10_2_2.py
import numpy as np
# statsmodels库的API，用于进行统计模型分析，并简称为sm。
import statsmodels.api as sm
# matplotlib库的一部分，用于绘图，并简称为plt。
import pylab as plt
# 使用numpy的loadtxt函数从文件data10_2.txt中加载数据。加载的数据被存储在数组a中。
a = np.loadtxt('data10_2.txt')
# usetex=False表示不使用LaTeX来渲染文本（因为LaTeX渲染可能需要额外的配置和字体支持）。
# font size=16设置字体大小为16。
plt.rc('text', usetex=False); plt.rc('font', size=16)
# plt.plot(a[0], a[2], '*', label='$x_1$'): 绘制一个散点图，
# 使用星号（*）作为标记，a[0]作为x轴数据，a[2]作为y轴数据，并为这组数据设置标签$x_1$。
plt.plot(a[0], a[2], '*', label='$x_1$')
print('a[0]:', a[0])
print('a[2]:', a[2])
# plt.plot(a[1], a[2], 'o', label='$x_2$'): 绘制另一个散点图，
# 使用圆圈（o）作为标记，a[1]作为x轴数据，a[2]作为y轴数据，并为这组数据设置标签$x_2$。
plt.plot(a[1], a[2], 'o', label='$x_2$')
# 显示图例，并将其位置设置为左上角。
plt.legend(loc='upper left')
# X = sm.add_constant(a[:2].T): 将a数组的前两行（a[:2]）转置（.T），
# 然后使用sm.add_constant函数为转置后的数组添加一个常数项（通常是1），
# 这是为了在线性回归模型中包含截距项。结果存储在X中。
X = sm.add_constant(a[:2].T)
# 使用statsmodels的OLS（普通最小二乘法）函数，
# 以a[2]作为因变量（响应变量），X作为自变量（预测变量），进行线性回归分析，
# 并通过.fit()方法拟合模型。拟合结果存储在re中。
re = sm.OLS(a[2], X).fit()
# 打印回归结果的摘要，包括系数、标准误、t值、p值、置信区间等信息。
print(re.summary())
# 使用拟合的回归模型对新的数据点进行预测。
# 这里预测了两个点：(9, 10)和(10, 9)（前面的1是为了包括截距项）。预测值存储在yh中。
yh = re.predict(np.array([[1,9,10],[1,10,9]]))
# 打印残差的方差（均方残差），这是模型拟合好坏的一个指标。
print('残差的方差:', re.mse_resid)
# 打印预测值。
print('预测值：', yh);
# 显示绘制的图形。
plt.show()

二、相关评价参数的解释

三、相关结果

1.X1/X2-Y的散点图

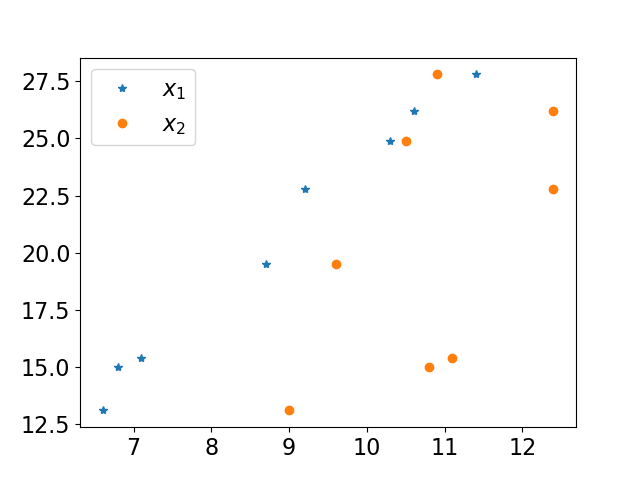
散点图说明X1、X2与Y有线性关系

2.评价参数