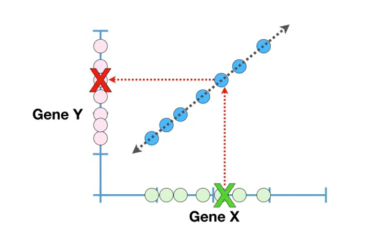
1. 相关系数(pearson' correlation)

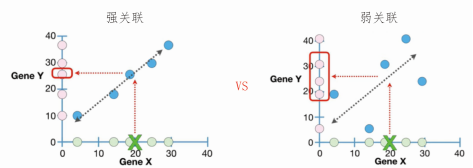
同时测量5个细胞中gene x与gene y的转录水平，将其绘制如下。将配对的数据用蓝色的小圆点表示，并使用直线展示gene x与gene y表达水平之间的相关趋势。基于该趋势，可以用gene x预测gene y的可能取值范围，也可用gene y预测gene x的可能取值范围。

• 「(左图)强相关」：如果基于gene x的表达量能够无偏差地预测gene y的表达量，说明二者之间有很强的联系；

• 「(右图)弱相关」：如果基于gene x的表达量不能较准确地预测gene y的表达量，说明二者之间仅有较弱的联系。

「注意不要过度推断因果关系」 根据结果，我们做出有根据的猜测(Educated guesses)，gene x的表达水平低，gene y倾向于低或高水平表达。但是gene x与gene y表达水平的高低之间无因果关系。如果有的话，一定要增加其他的数据证明。

以上涉及的是直线相关，相关系数的取值为【-1,1】:

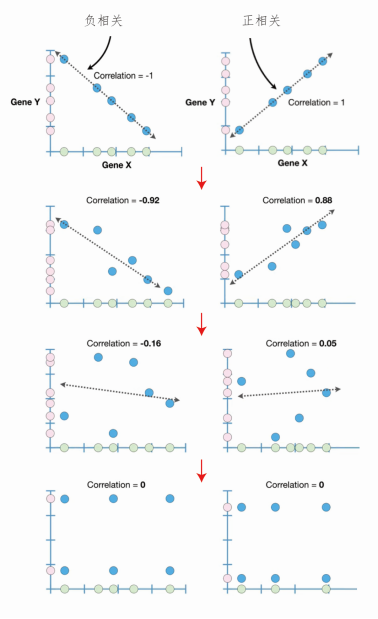
• 散点完全在同一条直线上，预测的准确性最高，相关系数的正负号表示相关性的正负。若x与y是同向变化，相关系数等于1，为完全正相关；若x与y是反向变化，相关系数等于-1，为完全负相关。
• 散点不完全在同一直线上，沿直线分布越集中，相关系数越接近1，预测准确性逐渐增加。相反，沿直线分布越分散，相关系数越接近0，预测的准确性逐渐减弱。
• 散点无相关性时，即x与y不相关时，相关系数为0，不能基于x预测y，也不能基于y预测x。

2. 相关系数与协方差的区别与联系

「协方差计算相关系数」

• 协方差的计算公式：

• 相关系数的计算公式：

  从上面的公式中可以看出：相关系数的计算公式中包括x与y的协方差、x的方差和y的方差。故计算x与y的协方差是计算相关系数的基础。分母的作用是将协方差的结果调整至[-1,1]，故相关系数不受数据scale的影响。

「相同点」：二者符号的正负代表两变量变化趋势是同向还是反向；

「差异点」：相关系数的取值与数据的scale无关，不论数据的多少，只要数据完全在同一条直线上(陡峭或者平缓)，相关系数就为1或者-1；而协方差取值对数据的scale敏感。这个原因使得协方差本身的意义难以阐释。

3. 相关系数与p值、预测能力

如果两个变量具有相关性，比如说他们的相关系数为0.8，那么他们之间的相关性是真实的吗？回答这个问题，也就是回答他们间的相关系数是否具有统计显著性，而统计中判断统计显著性的方法就是求p值。

「相关系数的p值：数据越多，p值越小，置信度越高。」 在统计学中，p值代表随机样本具有某种强度相关性(如r=0.8)或者较该强度更强相关性(r>0.8)的可能性。p值越小，置信度越高。

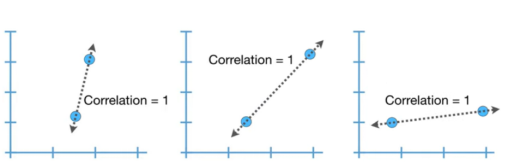
• 两个样本完全位于同一条直线上，我们不能利用该直线做可靠预测。因为任意2个样本构成一条直线，此时的p值=1。

• 3个样本位于同一直线上时，我们利用该直线做预测的可靠度增加。因为任意3个样本构成一条直线的概率相对较低，此时的p值较小。

• 更多的样本位于同一直线时，我们利用该直线做预测的可靠性进一步增加。因为多个样本位于同一直线的可能性更低，对应的p值更小。在该数据中，假设p值=2.2 x 10 -6，意味着随机样本存在该强度相关性或者更强强度相关性的概率非常小，仅为2.2 x 10 -6。

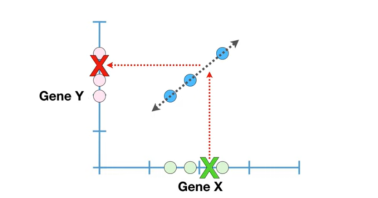
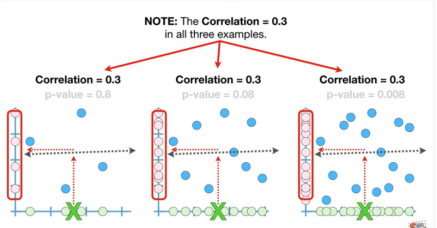
「相关系数与p值、预测能力：」 样本之间的相关系数小，仅为0.3，随着样本数据的增多，尽管p值逐渐增加，但样本间的相关系数不发生改变。这意味着在样本间相关系数较低的时候，增加数据也不能使我们的预测更加准确，增加样本仅仅增加我们对预测结果的信心(confidence)。具体而言，在3个样本量不同的数据中，我们的预测结果均不准确。在样本数量最多的数据中，即使我们对预测结果的信息很大，但预测依然比较糟糕。

4. 相关系数与R2

前面我们提及r越接近±1，直线的预测能力就越准确，但是如何量化不同r之间的预测准确性呢？如分别对r为0.7和0.5的数据做预测，是否前者的预测性能优于后者两倍？

这个问题很难再用相关系数进行回答，而应该用R²， R²=r x r。

• 如果r=0.9(显著)，则R² =0.81，说明两变量间的关系可以较好的解释数据的变异(也就是说，x与y的相关性可以解释81%y的变异)。
• 如果r=0.7(显著)，则R² =0.7 x 0.7=0.5，说明x与y的相关性可以解释50%y变异。
• 如果r=0.5(显著)，则R² =0.5 x 0.5=0.25，说明两变量间的关系不能较好解释变异，相反还有解释75%变异的其他因素。
• 对于r=0.7和r=0.5，前者R²是后者R²的2倍，故r=0.7的预测性能是r=0.5预测性能的两倍。

R²的计算与R²的意义：

1. 如果我们记录小鼠的大小和体重，并将其绘制在如下二维坐标中。考虑小鼠体积时的拟合效果(蓝色斜线)优于仅用小鼠体重均值数据(黑色水平线)拟合效果。这是因为小鼠体积和体重的关系可以解释一部分体重的变异。

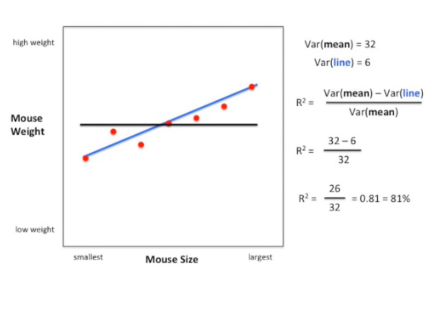
• 如何量化小鼠体积和体重关系解释的变异呢？这就需要用到R²。具体计算(公式见上方截图)：
• R²= 拟合直线解释的变异(VAR(mean)-VAR(fit))占均值变异(VAR(mean))的百分比
• 此处计算得出R²为81%，代表围绕拟合直线的变异较围绕均值变异少81%，表示由小鼠体积和体重关系解释的变异占体重总体变异的81%，说明小鼠体重的绝大部分变异可以由小鼠体积与小鼠体重的关系解释。

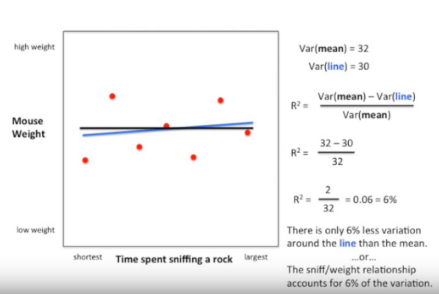
2. 如果我们分别记录小鼠做某件事(sniff a rock)的时间与小鼠的体重。

• 计算小鼠做某件事的时间与小鼠体重关系所解释小鼠体重变异的百分比，方法同前，R²=6%，围绕拟合直线的变异较围绕均值变异少6%，表示由小鼠做某件事时间和体重关系解释的变异占体重总体变异的6%，说明小鼠体重的绝大部分变异几乎不能由小鼠做某件事时间和体重关系所解释，相反可能存在其他解释的因素。

在上面的两个例子中，我们可以得出：变量间的关系也许可以完美解释其中一个变量的变化(小鼠体重与体积)，也许几乎不能揭示其中一个变量的变化(小鼠做某事的时间与小鼠的体重)。故R²取值范围[0,1]，这取决于相关系数r的取值范围为[-1,1]。

5.小结

在本小节中，我们进一步了解了相关系数与协方差的关系，通过p值来评估r与R²的可信度，随后我们也了解了R²可以量化不同相关系数r之间的预测准确性。本小节基本概念较多，需要掌握的伙伴可以观察本小节涉及的原视频(下方链接或B站关键字搜索)，同时也要多多查阅书籍。

参考视频：

1. https://www.youtube.com/watch?v=qtaqvPAeEJY&list =PLblh5JK OoLUK0FLuzwntyYI10UQFUhsY9&index=15

2. https://www.youtube.com/watch?v=xZ_z8KWkhXE&list =PLblh5JK OoLUK0FLuzwntyYI10UQFUhsY9&index=16

3.https://www.youtube.com/watch?v=2AQKmw14mHM&list=PLblh5JKOoLUK0FLuzwntyYI10UQFUhsY9&index=17

●相关阅读●

协方差(covariance)与相关系数(1)|统计学专题

为什么除以n会低估总体方差？| 统计学专题

总体参数与样本估计总体参数]统计学专题

正态分布与中心极限定理|统计学专题