pytorch深度学习框架CUDA版本环境安装记录——牛刀杀鸡——解一个非线性方程组
在深度学习界pytorch框架用得人越来越多,无论是CV机器视觉、NLP还是自然语言处理,目前主流的大的模型如GPT模型等也很多用pytorch。比如清华大学的单机GPT模型chatGLM,用的是GPU版本的pytorch。本人以前用的时keras,第一次装pytorch,记录一下安装的步骤,便于以后参考。
一、前言
在深度学习界pytorch框架用得人越来越多,无论是CV机器视觉、NLP还是自然语言处理,目前主流的大的模型如GPT模型等也很多用pytorch。比如清华大学的单机GPT模型chatGLM,用的是GPU版本的pytorch。本人以前用的时keras,第一次装pytorch,记录一下安装的步骤,便于以后参考。
二、安装步骤
step1. 安装显卡驱动
显卡主是要用英伟达的显卡。根据显卡的型号去英伟达官网进行下载安装
step2. 安装cuda
此步也一样,都是去官网cuda相关页面下载对应的显卡、操作系统的版本: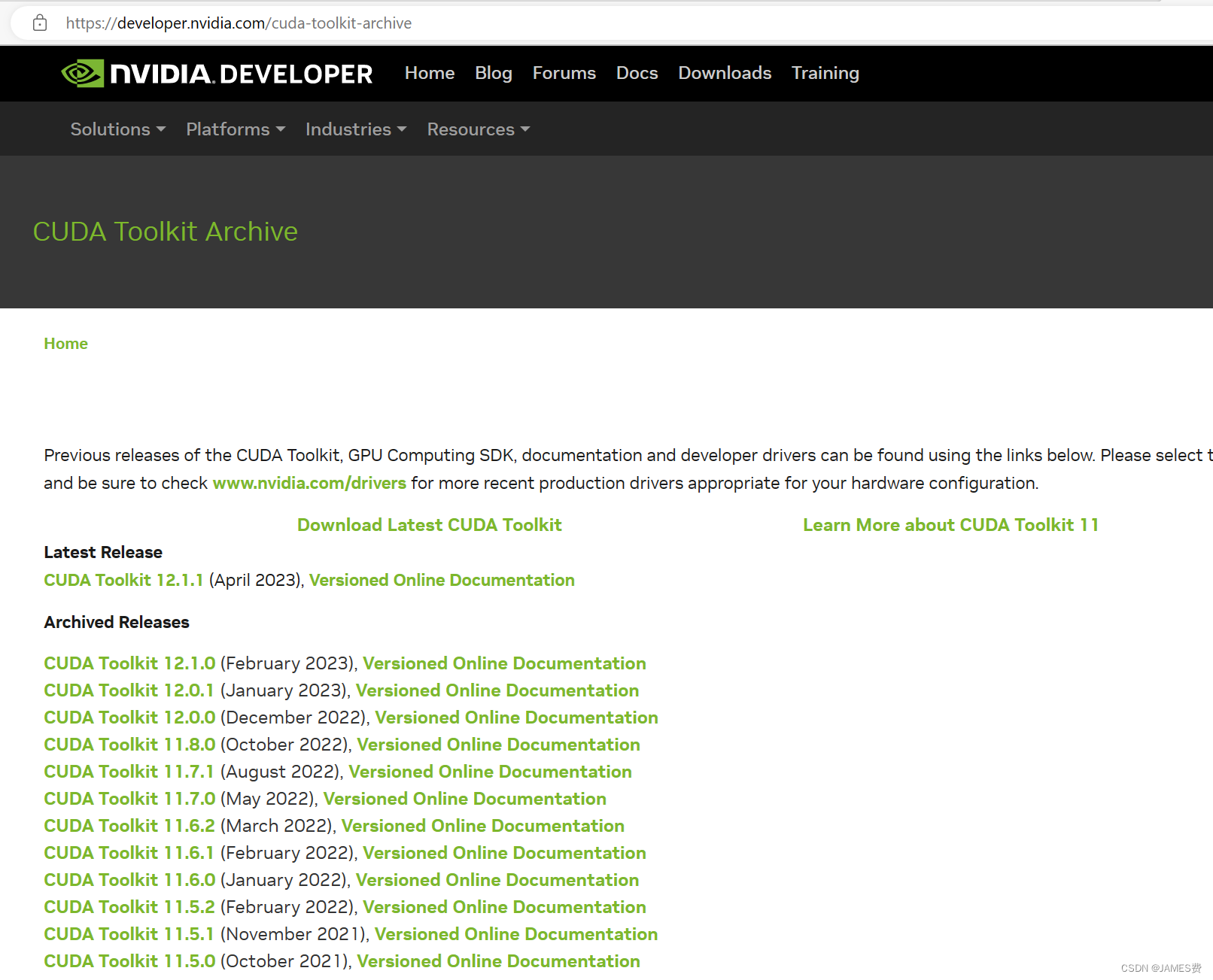
本人下了12.1
下载完就双击安装,跟一般软件一样。
step3. 安装cuDNN
此步也一样,都是去官网cuDNN相关页面下载对应的显卡、操作系统的版本: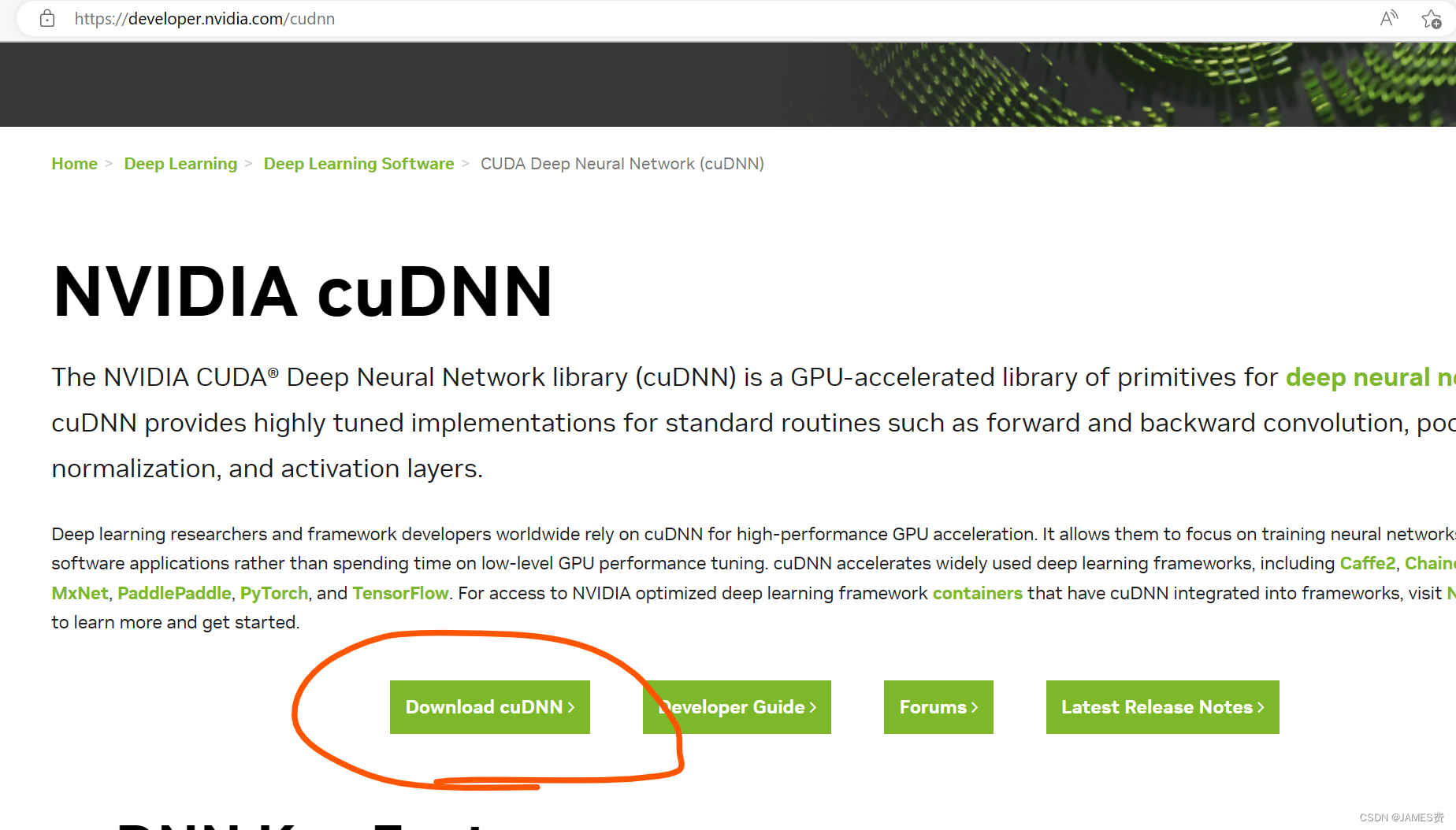
这里第一次进去可能要求注册个人的账号,有点费劲,根据引导注册就好。
注册好后,选择适合自己的操作系统版本下载。
下载好后解压出几个文件夹,: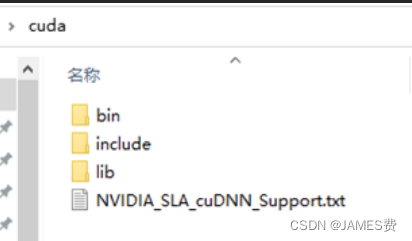
找到cuda的安装目录,讲对应的文件夹给替换了。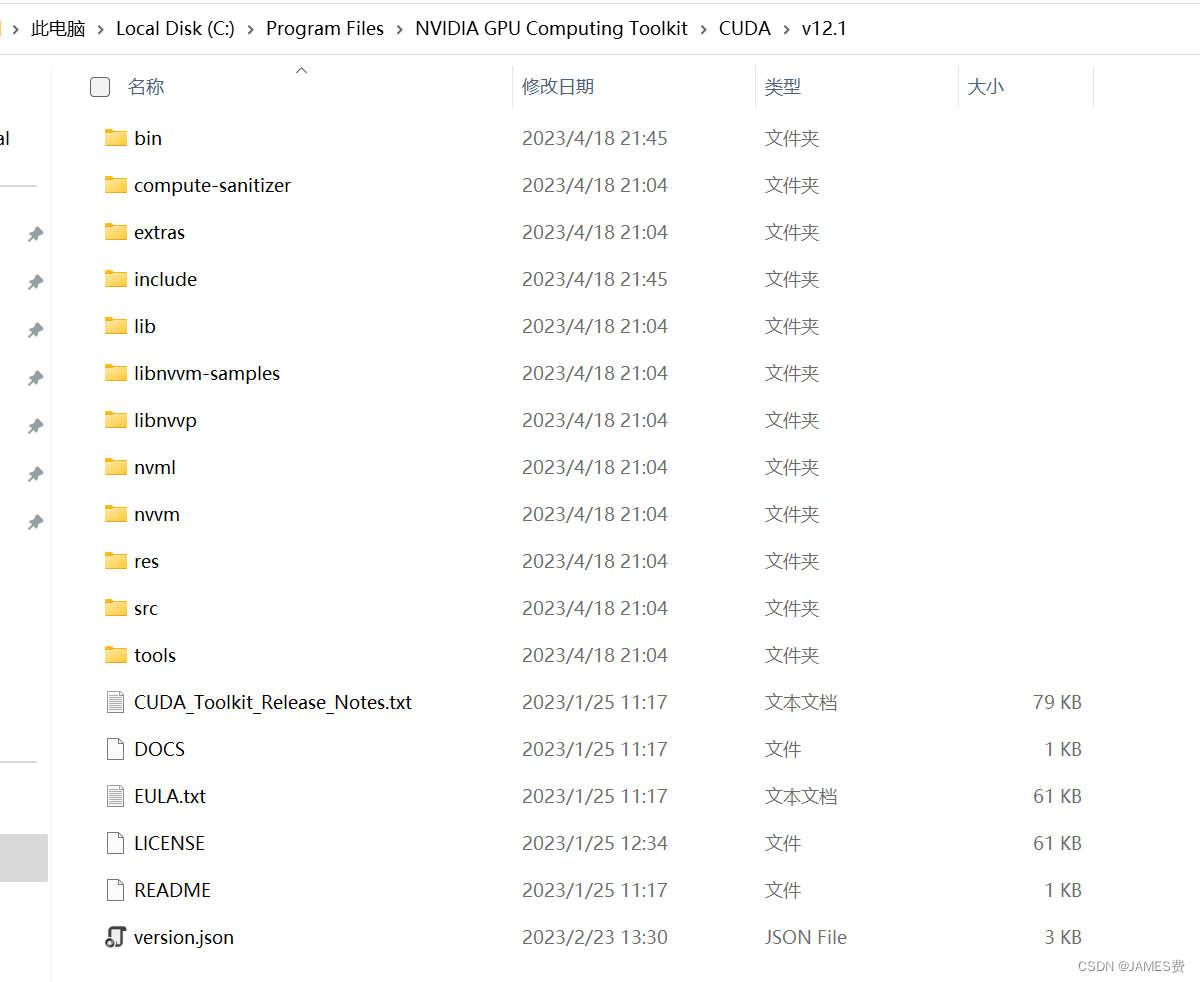
验证cuDNN是否安装完成,打开cmd,输入
cd C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v12.1\extras\demo_suite
然后执行命令:
bandwidthTest.exe
出现PASS,就说明成功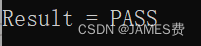
step4. 安装pytorch环境
网速快的话可以安装pytorch的官网说明安装(不建议):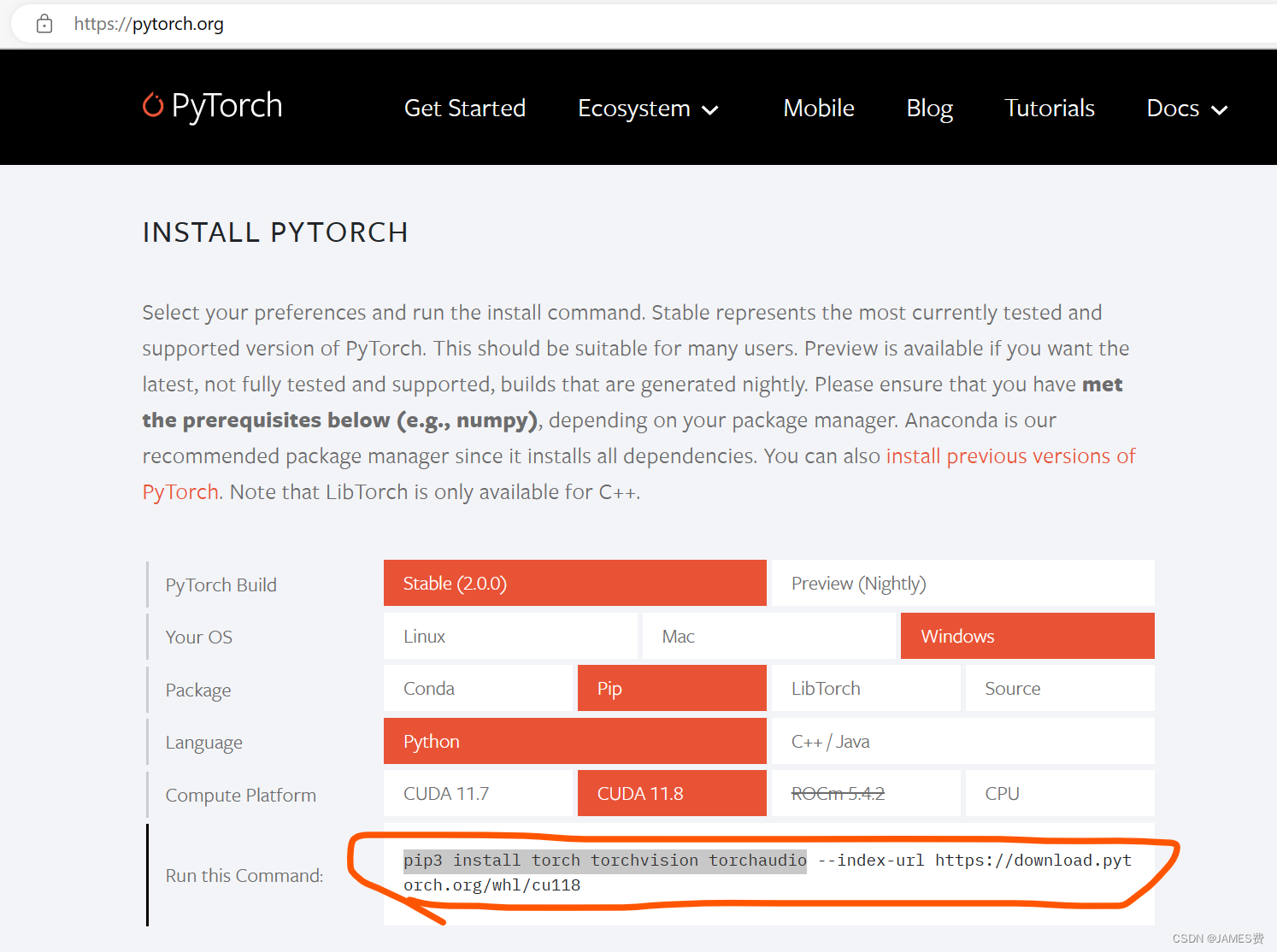
由于torch的尺寸有点大,由于网络等原因通过pip指令下载可能会timeout,最好去相应的网页手动下载相应的模块,主要涉及三个模块:torch、torchvision、torchaudio这三个。
这三个模块要选择对应的配套版本,以下是torch版本分别对应torchvision、torchaudio的对应关系: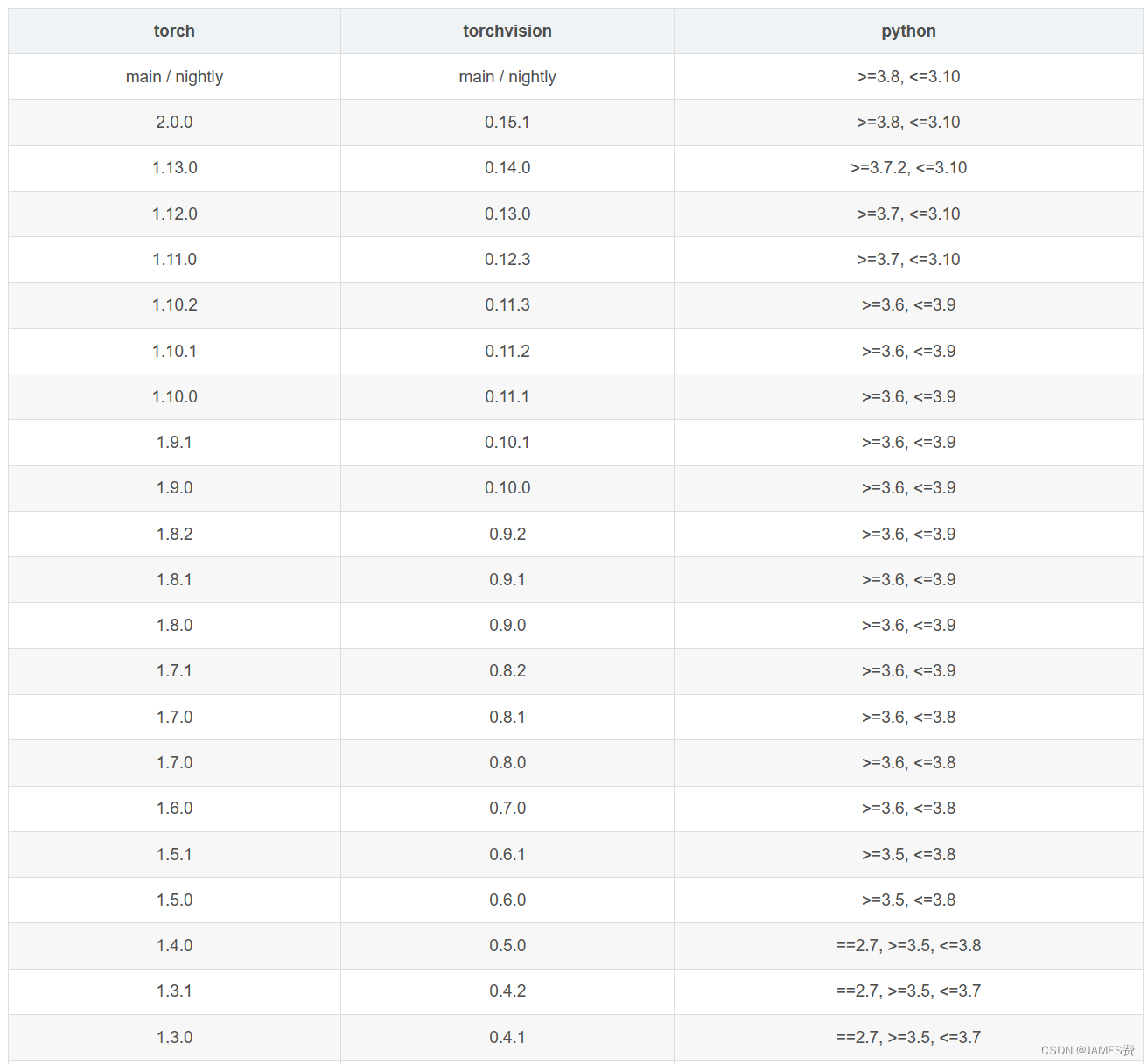
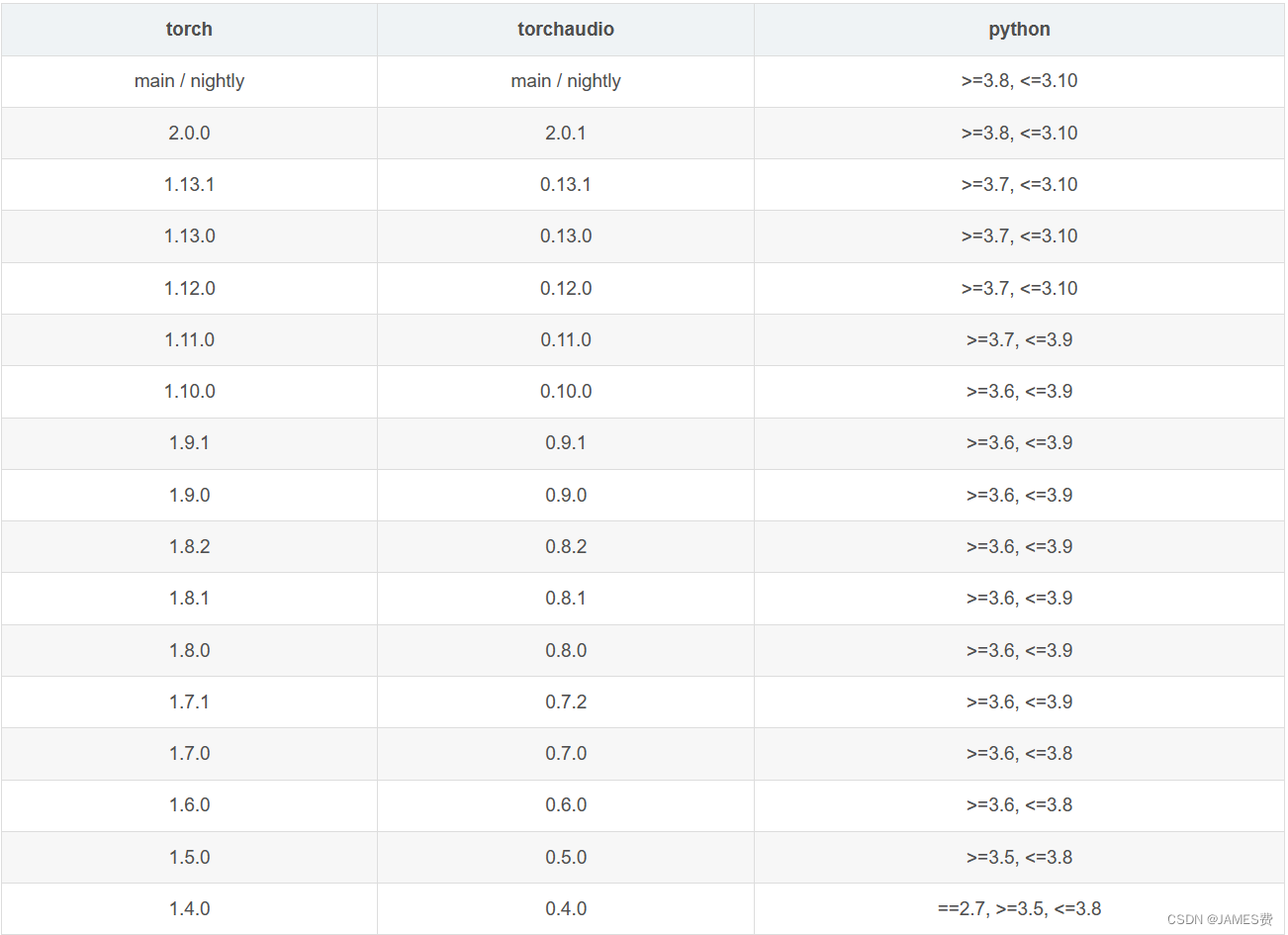
最保险的安装方法是先离线下好这三个文件,网址为:离线下载链接
这里,上面我下载的cuda的版本是12.1,还没有一样的版本,于是我下载了最高的版本11.8(即,cu118开头的):
例如:cu118/torch-2.0.0%2Bcu118-cp39-cp39-win_amd64.whl
cu118——代表cuda 11.8版本
torch-2.0.0——代表2.0.0版本
cp39——代表python 3.9版本
win_amd64——代表windows 64位
查表对应的torchvision、torchaudio版本为:0.15.1和2.0.1
下载完三个离线文件后,进入文件所在目录,通过pip install指令安装( pip install torch-2.0.0+cu118-cp39-cp39-win_amd64.whl torchaudio-2.0.1+cu118-cp39-cp39-win_amd64.whl torchvision-0.15.1+cu118-cp39-cp39-win_amd64.whl),不一会就安装完成了: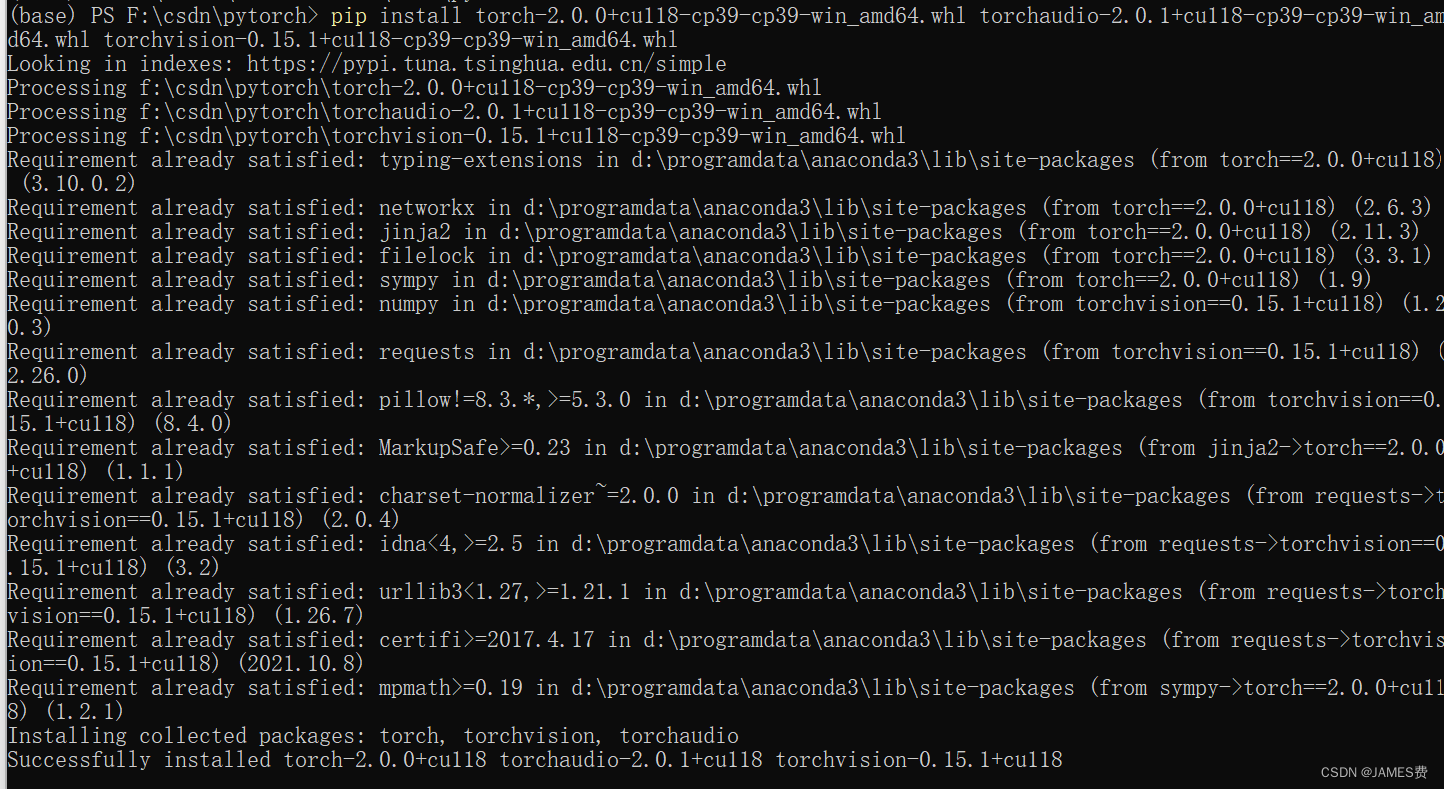
三、用pytorch解个非线性方程组
利用pytorch的图计算框架,反向传播机制,可以很容易对非线性方程组求解,当然这里是用牛刀杀鸡了:
import torch
# Define the equations as functions
def f1(x, y):
return x**2 + y**2 - 1
def f2(x, y):
return x - y**2
# Define the variables
x = torch.tensor([1.0], requires_grad=True)
y = torch.tensor([1.0], requires_grad=True)
# Define the optimizer
optimizer = torch.optim.Adam([x, y], lr=0.1)
# Define the loss function
def loss_fn(x, y):
return f1(x, y)**2 + f2(x, y)**2
# Train the model
for i in range(1000):
optimizer.zero_grad()
loss = loss_fn(x, y)
loss.backward()
optimizer.step()
# Print the results
print("x: ", x.item())
print("y: ", y.item())
感觉这个可以实现工程化,只要列出方程组,就可以用以上类似的方法求解。
运行如下(误差非常小):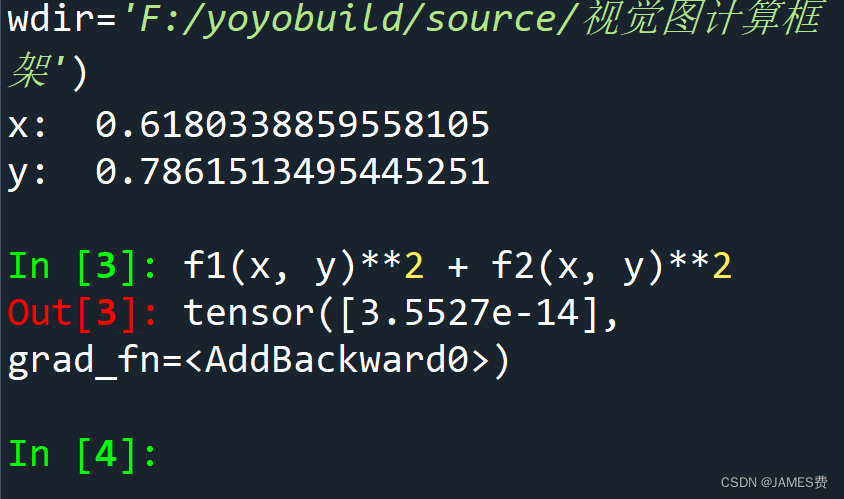

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容






所有评论(0)