最近在看斋藤康毅的《深度学习入门：基于Python的理论与实现》 ，以下按章节做一点笔记。

01 第五章 误差反向传播法

之前章节实现的方法是数值微分，容易实现，但是很费时间。
本章引入一个高效计算权重参数的梯度的方法–误差反向传播法。
理解方法有两种，一是基于数学式（比较常见）；二是基于计算图。
本章主要是从计算图这一方法讲解。

1.1 计算图

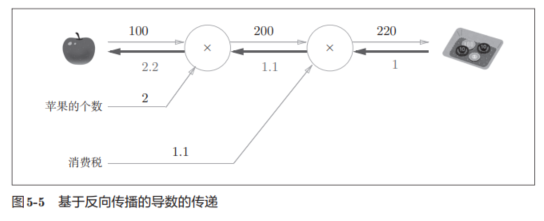
假设我们想知道苹果价格的上涨会在多大程度上影响最终的支付金额，即求“支付金额关于苹果的价格的导数”。

反向传播使用与正方向相反的箭头（粗线）表示。
反向传播传递“局部导数”，将导数的值写在箭头的下方。

• 在这个例子中，反向传播从右向左传递导数的值（1 → 1.1 → 2.2）。从这个结果中可知，“支付金额关于苹果的价格的导数”的值是2.2。
• 说明，如果苹果的价格上涨1日元，最终的支付金额会增加2.2日元。
  其他导数也可以用类似方法。

1.2 反向传播

反向传播本质上是利用的链式法则和局部求导。
假设有，z = (x+y)^2
其中z=t^2， t=x+y。计算图如下：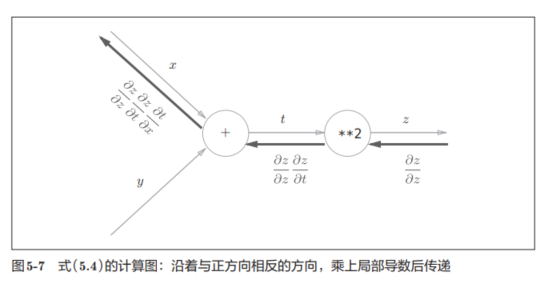

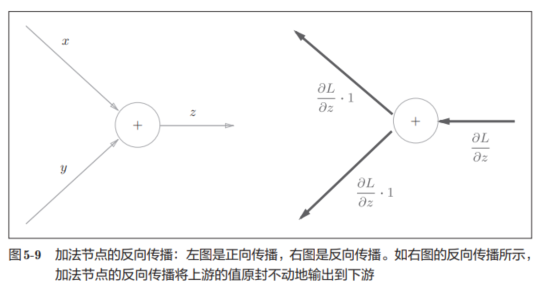
1.2.1 加法节点的反向传播

若有z = x + y，易得：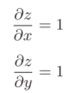

则可得到下面的计算图，且假设Z进行某种计算才得到L：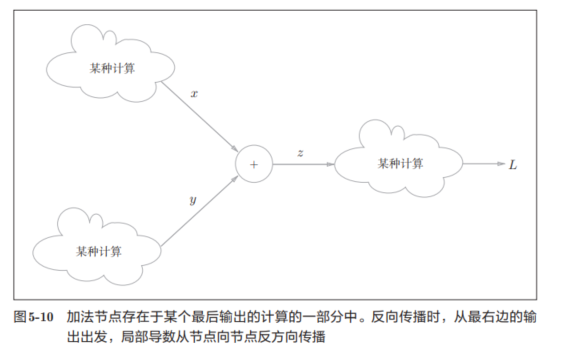

1.2.2 乘法节点的反向传播

在这里假设z=xy，得到下面的偏导数：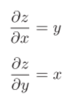

得到的计算图变成这样：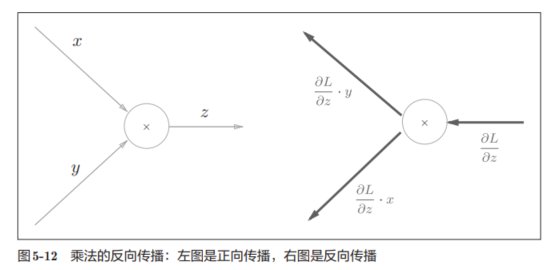

1.2.3 简单层的实现

有了上面理解后很容易得到，乘法层的实现为：

class MulLayer:# 乘法层
    def __init__(self):
        self.x = None
        self.y = None

    def forward(self, x, y):# 前向传播
        self.x = x
        self.y = y                
        out = x * y

        return out

    def backward(self, dout):# 反向传播
        dx = dout * self.y
        dy = dout * self.x

        return dx, dy

用这个乘法层，来实现之前1.1 中购买两个苹果需要付的钱的代码为：

apple = 100
apple_num = 2
tax = 1.1

# layer
mul_apple_layer = MulLayer()
mul_tax_layer = MulLayer()

# forward
apple_price = mul_apple_layer.forward(apple, apple_num)
price = mul_tax_layer.forward(apple_price, tax)

print(price) # 220

关于各个变量的导数也可以用backward()求出

# backward
dprice = 1
dapple_price, dtax = mul_tax_layer.backward(dprice)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)

print(dapple, dapple_num, dtax) # 2.2 110 200

同理，加法层的实现为：

class AddLayer:
    def __init__(self):
        pass
    def forward(self, x, y):
        out = x + y
        return out
    def backward(self, dout): 
        dx = dout * 1
        dy = dout * 1
        return dx, dy

下面有个新案例，要购买2个苹果和3个橘子：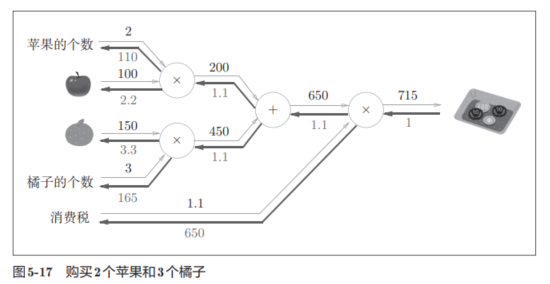

实现代码如下，虽然看着跺，但是逻辑非常简单，注意命名别混乱了。

# 实现买两个苹果+三个橘子的案例
apple = 100
apple_num = 2
orange = 150
orange_num = 3
tax = 1.1

# layer
mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()

# forward
apple_price = mul_apple_layer.forward(apple, apple_num) #(1)
orange_price = mul_orange_layer.forward(orange, orange_num) #(2)
all_price = add_apple_orange_layer.forward(apple_price, orange_price) #(3)
price = mul_tax_layer.forward(all_price, tax) #(4)

# backward
dprice = 1
dall_price, dtax = mul_tax_layer.backward(dprice) #(4)
dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price) #(3)
dorange, dorange_num = mul_orange_layer.backward(dorange_price) #(2)
dapple, dapple_num = mul_apple_layer.backward(dapple_price) #(1)

print(price) # 715
print(dapple_num, dapple, dorange, dorange_num, dtax) # 110 2.2 3.3 165 650

1.2.4 激活函数实现

上述表述，还没有加入激活函数，在实际中我们还会用到激活函数。

1.2.4.1 ReLU

下面是ReLU的代码：

class Relu:
    def __init__(self):
        self.mask = None
        
    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0
        return out
    
    def backward(self, dout): 
        dout[self.mask] = 0
        dx = dout
        return dx

关于部分代码的解释：


上面解释很好。反向传播时，也需要进行x与0的大小比较，这里直接用前向传播保留的self.mask就好了。

1.2.4.2 sigmoid

关于sigmoid，表达式和计算图为：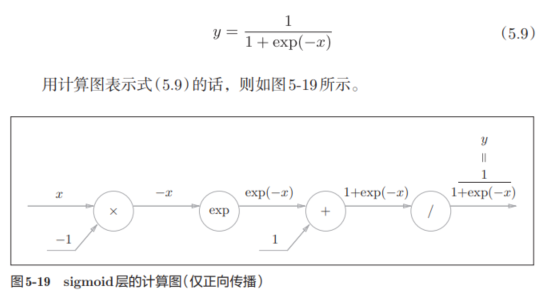

则反向传播的过程如下，如果有不懂可以看原书，在p141-143。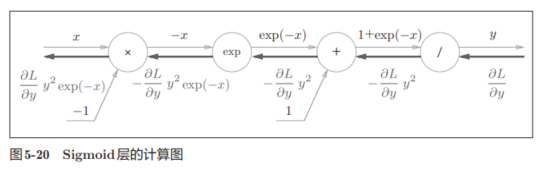

所以简化一下，即有：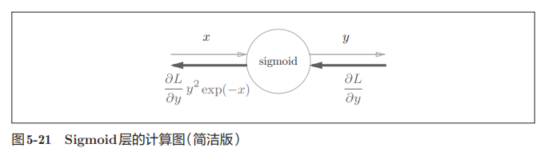

对表达式进行整理：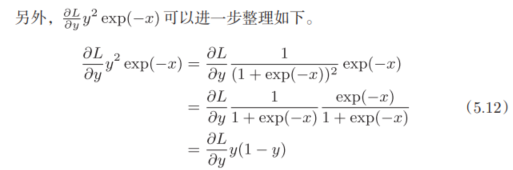


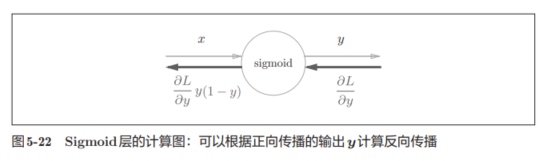
所以得到sigmoid的实现代码：

class Sigmoid:
    def __init__(self):
        self.out = None
        
    def forward(self, x):
        out = 1 / (1 + np.exp(-x))
        self.out = out
        return out
    
    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out 
        return dx

1.2.4.3 Affine层

Affine 层（仿射层）是神经网络中最基本的一类“全连接层”或“线性层”

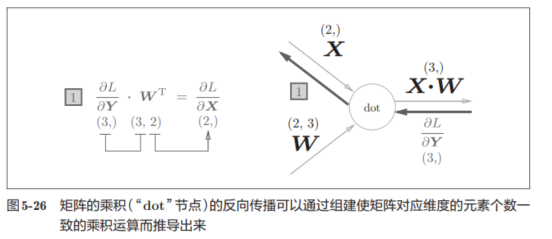
举一个例子，维度在图中标出：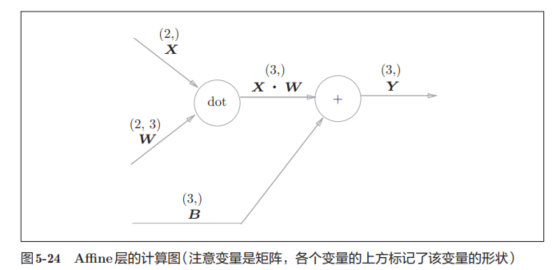

得到的表达式为，其中有转置是为了形状对应上：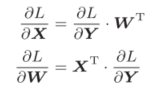

可以尝试看看反向的形状对应：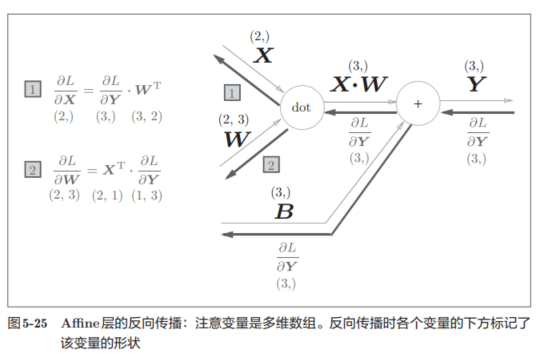

L对X的偏导本来就衡量的是X的变化对L的影响，所以维度应当是和X一样的。

之前的X事一耽搁数据为对象的，现在考虑N个数据一起（如一次训练，许多图片达成一批进行训练），分析图为：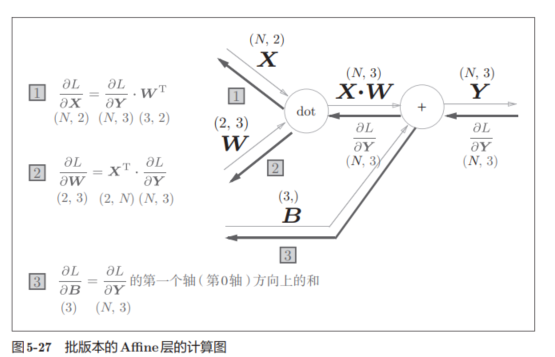

基本逻辑是保持不变的。
特别注意，反向传播时，对偏置的偏导数！
实现代码为：

class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        self.x = None
        self.dW = None
        self.db = None
        
    def forward(self, x):
        self.x = x
        out = np.dot(x, self.W) + self.b 
        return out
    
    def backward(self, dout):
        dx = np.dot(dout, self.W.T)
        self.dW = np.dot(self.x.T, dout) 
        self.db = np.sum(dout, axis=0)
        return dx

1.2.4.4 softmax

softmax函数会将输入值正规化之后再输出。（注意是正规化，不是正则化，和正则化概念区分–正规化处理输入，正则化防止过拟合）
比如手写数字识别时，Softmax层的输出如下：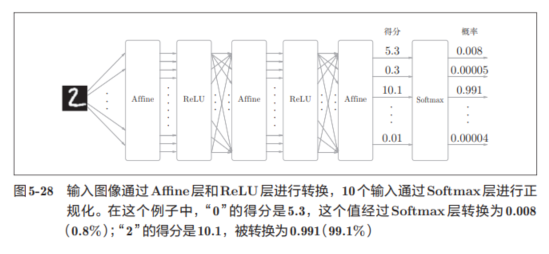

因为手写数字识别要进行10类分类，所以向Softmax层的输入也有10个。

Softmax-with-Loss 层通常就是指 Softmax 函数 + 交叉熵损失函数 的组合
这两个函数合在一起有很多好处，尤其是可以简化反向传播的计算，数值更稳定，梯度表达更简洁。
书上进行了计算图的一个粗略表示：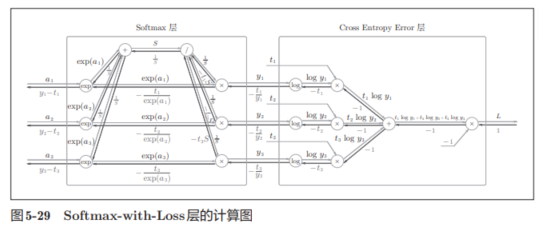

进行简化为：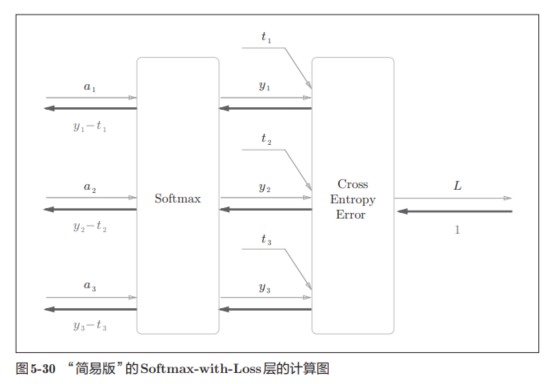

其中，Softmax层将输入（a1, a2, a3）正规化，输出（y1, y2, y3）。Cross Entropy Error层接收Softmax的输出（y1, y2, y3）和教师标签（t1, t2, t3），从这些数据中输出损失L。
反向传递求起来比较复杂，详细可见本书附件（如果有时间，我到时候看了也整理一下）。

由于（y1, y2, y3）是Softmax层的输出，（t1, t2, t3）是监督数据，所以（y1 − t1, y2 − t2, y3 − t3）是Softmax层的输出和教师标签的差分。
神经网络的反向传播会把这个差分表示的误差传递给前面的层。

书中提到的有意思的一点：

代码实现为，利用了之前实现的softmax()和cross_entropy_error()函数：

class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None # 损失
        self.y = None # softmax的输出
        self.t = None # 监督数据（one-hot vector）
    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t) 
        return self.loss
    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        dx = (self.y - self.t) / batch_size
        return dx

注意反向传播时，将要传播的值除以批的大小（batch_size）后，传递给前面的层的是单个数据的误差。