建议先阅读我之前的深度学习博客，掌握一定的深度学习前置知识后再阅读本文，链接如下：

带你从入门到精通——深度学习（一. 深度学习简介和PyTorch入门）-CSDN博客

带你从入门到精通——深度学习（二. PyTorch中的类型转换、运算和索引）-CSDN博客

带你从入门到精通——深度学习（三. PyTorch中张量的形状重塑、拼接和自动微分）-CSDN博客

带你从入门到精通——深度学习（四. 神经网络的概念、激活函数和参数初始化）-CSDN博客

目录

五. 神经网络的搭建、损失函数和反向传播

5.1 PyTorch中神经网络的搭建

5.2 损失函数

5.2.1 分类任务损失函数

5.2.2 回归任务损失函数

5.3 反向传播

5.3.1 梯度下降算法

5.3.2 反向传播详解

---

五. 神经网络的搭建、损失函数和反向传播

5.1 PyTorch中神经网络的搭建

        在PyTorch中定义神经网络其实就是各种网络层（layer）的堆叠过程，我们定义的神经网络类需要继承自torch.nn.Module，并且需要实现两个方法：一是实现__init__方法，该方法用于定义神经网络中的各个层结构并进行初始化；二是实现forward方法，该方法用于定义神经网络的前向传播逻辑，当你对一个继承了torch.nn.Module的实例对象进行调用时（例如model(input)的格式，model为一个继承了torch.nn.Module的实例对象），会自动调用该实例所属类的__call__方法，而__call__方法的内部则会调用forward方法。

        总结来说，PyTorch中神经网络的搭建过程就是“一个继承，两个方法”。

        神经网络模型的搭建实例如下：

import torch
import torch.nn as nn
from torchsummary import summary

# 继承父类nn.Module
class Modal(nn.Module):
    def __init__(self):
        # 在__init__方法中定义神经网络的各个网络层
        # 该模型由3个全连接层组成，其中2个隐藏层，1个输出层
        super(Modal, self).__init__()
        self.fc1 = nn.Linear(3, 4, bias=False)
        nn.init.xavier_normal_(self.fc1.weight) # 正态分布的xavier初始化
        self.fc2 = nn.Linear(4, 2)
        nn.init.kaiming_normal_(self.fc2.weight) # 正态分布的kaiming初始化
        self.out = nn.Linear(2, 3)
    # 定义forward方法，在方法定义神经网络的前向传播逻辑
    def forward(self, x):
        x = self.fc1(x)
        x = torch.sigmoid(x) # 使用sigmoid激活函数
        x = self.fc2(x)
        x = torch.relu(x) # 使用relu激活函数
        x = self.out(x)
        x = torch.softmax(x, dim=-1) # 使用softmax激活函数，输出最后的分类概率
        return x

if __name__ == '__main__':
    modal = Modal().to('cuda') # 实例化神经网络对象并将模型加载到GPU上
    x = torch.randn(6, 3).to('cuda') # 创建一个随机输入张量x并将其加载到GPU上
    out = modal(x) # 将输入张量x输入到神经网络中，得到输出张量out
    # 使用torchsummary库查看模型参数和模型结构
    # 定义输入尺寸为(3,)，batch_size为6
    summary(modal, (3,), 6) 
    '''
    ----------------------------------------------------------------
            Layer (type)               Output Shape         Param #
    ================================================================
                Linear-1                     [6, 4]              12
                Linear-2                     [6, 2]              10
                Linear-3                     [6, 3]               9
    ================================================================
    Total params: 31
    Trainable params: 31
    Non-trainable params: 0
    ----------------------------------------------------------------
    Input size (MB): 0.00
    Forward/backward pass size (MB): 0.00
    Params size (MB): 0.00
    Estimated Total Size (MB): 0.00
    ----------------------------------------------------------------
    '''

        注意：全连接层只能接收二维数据集，即第一个维度为batch_size，第二个维度为feature的数据集。

5.2 损失函数

        在深度学习中，损失函数是用来衡量模型参数的质量的函数，衡量的方式是比较网络输出和真实输出的差异，损失函数在不同的文献中的名称是不一样的，但本质都是指同一个东西，主要有以下几种命名方式：

5.2.1 分类任务损失函数

        在多分类任务的输出层，通常使用softmax函数将逻辑值logits转换为概率值，最后使用交叉熵损失（也称log loss）函数来衡量模型参数的质量，对于多分类任务来说，交叉熵损失也可以叫做softmax损失，其计算方法如下：

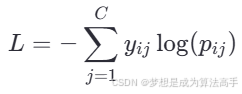
        其中pij​是第i个样本属于类别j的概率值，yij是样本i属于类别j的真实概率（0或1）。

        在pytorch中多分类的交叉熵损失使用torch.nn.CrossEntropyLoss()实现，该api会将输出层的值先使用softmax函数转换为概率值之后再计算交叉熵损失，因此输出层可以不加softmax函数作为激活函数。

        而在二分类任务的输出层，通常使用sigmoid函数将逻辑值logits转换为概率值，最后同样使用交叉熵损失（也称log loss）函数来衡量模型参数的质量，对于二分类任务来说，其计算方法可以简化为如下形式：

        其中yi是当前样本的真实标签（0或1），pi是当前样本属于正类的概率值。

        在pytorch中二分类的交叉熵损失使用torch.nn.BCELoss()实现，该api会将输出层的值先使用sigmoid函数转换为概率值之后再计算交叉熵损失，因此输出层可以不加sigmoid函数作为激活函数。

5.2.2 回归任务损失函数

        MAE和MSE在机器学习的线性回归章节有详细介绍，这里只做简单总结。

        平均绝对误差（Mean Absolute Error，MAE）也被称为L1 Loss，该损失函数具有稀疏性，能够惩罚数值过大的参数，因此常常将其作为正则项添加到其他损失函数中，但L1 loss的最大问题是梯度在零点不平滑，可能会跳过极小值，其函数图像如下：

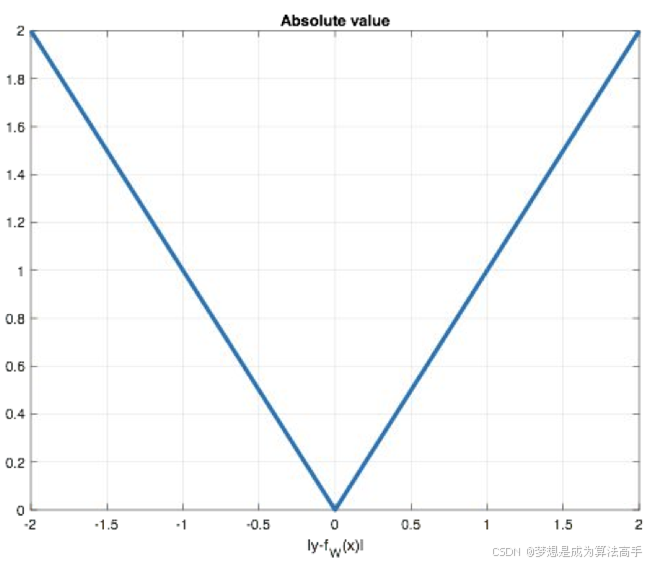
        在pytorch中MAE使用torch.nn.L1Loss()实现。

        均方误差（Mean Squared Error，MSE）也被称为L2 loss，L2 loss也常常作为正则项添加到其他损失函数中，但当预测值与目标值相差很大时，使用L2 loss容易出现梯度爆炸的问题，其函数图像如下：

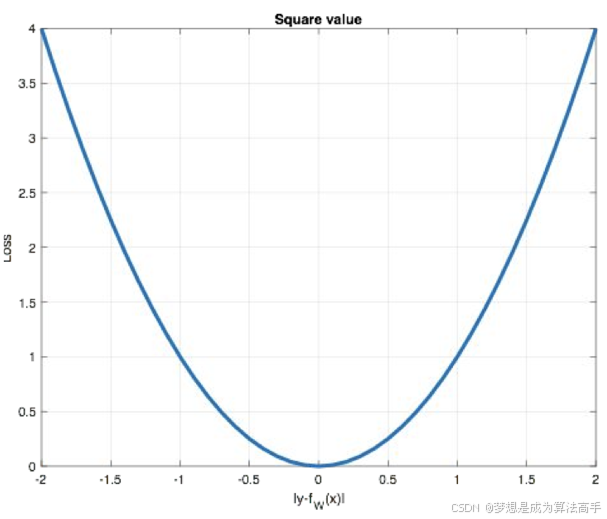
        在pytorch中MSE使用torch.nn.MSELoss()实现。

        smooth L1 loss是指对零点进行平滑之后的L1 loss，其函数表达式如下：

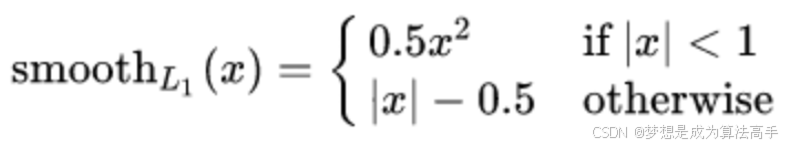
        其中x即为真实值和预测值的差值。

        三种损失函数的图像对比如下：

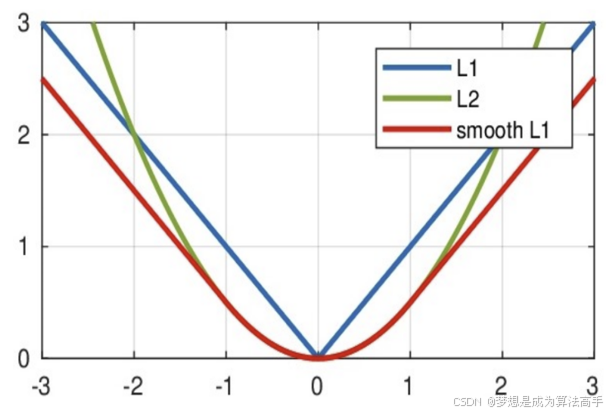
        从上图中可以看出，smooth L1 loss实际上就是一个分段函数，在[-1,1]区间内类似于L2 loss，解决了L1 loss的零点不光滑问题，在[-1,1]区间外，类似于L1损失，解决了L2 loss的离群点梯度爆炸问题。

        在pytorch中MSE使用torch.nn.SmoothL1Loss()实现。

5.3 反向传播

5.3.1 梯度下降算法

        梯度下降算法是神经网络反向传播的基础，在机器学习的线性回归章节有详解介绍，这里只做简要介绍，梯度下降法一种寻找使损失函数最小值的方法，从数学上的角度来看，梯度的方向是函数增长速度最快的方向，那么梯度的反方向就是函数减少最快的方向，因此神经网络模型的参数更新公式如下：

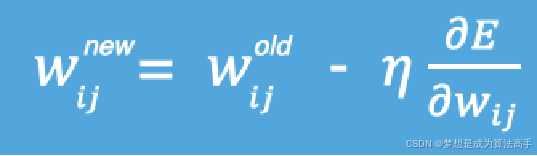
        在进行模型训练时，有三个基础的概念：

        Epoch：指训练轮次，使用全部数据对模型进行一次完整训练即为一个epoch。

        Batch_size：指一次训练（一次参数更新）中，使用的样本数量，设置batch_size的目的是使用训练集中的小部分样本对模型的参数进行更新。

        Iteration：指使用一个batch_size的数据对模型进行一次参数更新的过程。

5.3.2 反向传播详解

        在神经网络中，前向传播指的是将数据输入的神经网络中，逐层向前传输，一直到运算到输出层为止，而反向传播（Back Propagation，BP）则是指从后往前使用链式求导法则，依次求损失函数对各个参数的偏导，结合梯度下降算法进行参数更新的过程。

        假设我们有如下的神经网络模型：

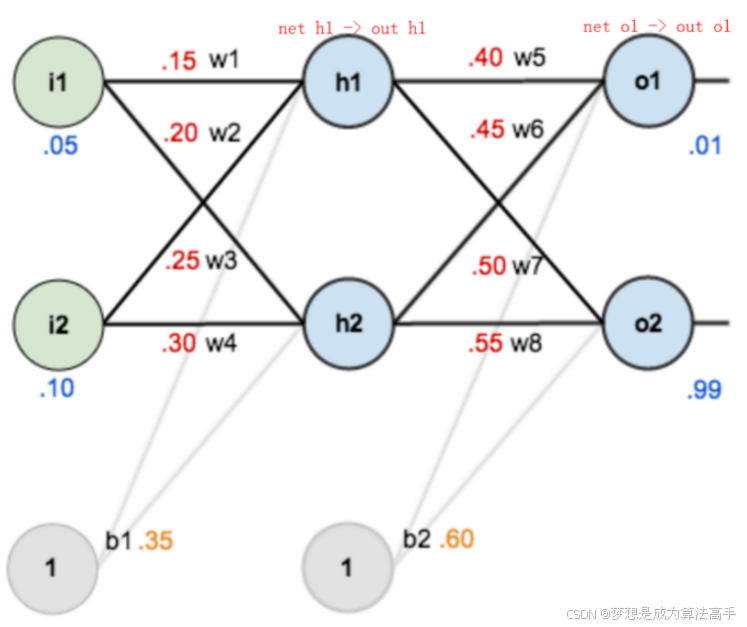
        参数w5的梯度计算方法如下：

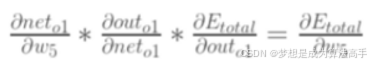
        参数w1的梯度计算方法如下：

        上述公式中的o包含o1和o2。