量子计算 笔记1 —— 量子比特

试图简单的理解一下量子比特的原理，定义的动机

相量法

高中时期，表示一个三角类函数 $f(t)=a\cos (\omega t+\alpha )$

这里使用一种新的方式

利用$e^{jx}=\cos x+j\sin x$
$$f(t)=\text{Re}\left[a{e}^{j(\omega t+\alpha )}\right]=\text{Re}\left[a{e}^{j\omega t}{e}^{j\alpha }\right]$$
$\text{Re}[c]$表示c的实数部分，$\text{Im}[c]$表示虚数部分，则其中这个函数的初相角就可以用$e^{j\alpha }$表示

则对于函数$F(t)=a{e}^{j\omega t}$，他在任意时刻，模长为$a$，他的实部（即复数向量在实轴的投影）即为一个三角类函数

若要改变$F(t)$的相位，只需乘上$e^{j\alpha }$，可以使相位角改变$\alpha$

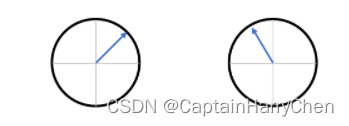
用圆的半径来表示波函数的振幅，箭头的角度来表示相位

概率波

在量子力学中，一个粒子的状态是不确定的，在空间和时间中呈现概率的形态，只有观测时才会根据概率选择一个状态，被我们观测到。

经过大量的实验观测和统计，一群牛逼的科学家整理出一个规律：

比如对一个电子，有一个奇怪的复函数$\Phi (\mathbf{r},t)$，其中$\mathbf{r}$为空间位置，$t$为时间

然后发现复函数在$({\mathbf{r}}_0,t_0)$处的模长平方，即$|\Phi ({\mathbf{r}}_0,t_0){|}^2$，为电子在该空间位置和时间出现的概率

概率越大，电子打在该位置越多，就会形成亮斑

然后用双缝干涉实验，观测到了干涉现象，说明$\Phi (\mathbf{r},t)$是一个波函数，那么其也可用$\Phi (\mathbf{r},t)=f(\mathbf{r},t)e^{j\omega (...)}$的方式表示

量子比特

对于传统计算机的比特，只有0和1两个状态，一般用高电压和低电压来表示

但经过量子力学的研究，我们也许可以找到一个神奇的东西（比如电子、光子等诡异的东西），具有一个波函数$\Phi (\mathbf{r})$。

让这个东西，被观测时呈现的两个完全不一样的（正交的）状态分别表示0和1，这两个状态分别表示为$|0⟩,|1⟩$，比如电子是否出现在该位置。

电子不出现的概率表示用波函数表示可能为${\Phi }_0({\mathbf{r}}_0)=a{e}^{j\eta },a为振幅,\eta 为相位$，那么该不出现的概率为$|{\Phi }_0({\mathbf{r}}_0){|}^2=a^2$

同理电子出现在该位置${\Phi }_1({\mathbf{r}}_0)=b{e}^{j\varphi },b为振幅,\varphi 为相位$，那么该不出现的概率为$|{\Phi }_1({\mathbf{r}}_0){|}^2=b^2$

显然必须满足$a^2+b^2=1$

一个电子有一定概率出现，有一定概率不出现，把这种情况作为一个量子比特，定义为
$$|\psi ⟩=a{e}^{j\eta }|0⟩+b{e}^{j\varphi }|1⟩$$
但实际上，知道两个状态的相位是没有意义的，我们只需要两个状态的相位差就可以了。所以可以把定义修改为
$$|\psi ⟩=a|0⟩+b{e}^{j\varphi }|1⟩$$
由于$a,b$满足$a^2+b^2=1$

那么其实可以把$a,b$换为角度表示，定义修改为
$$|\psi ⟩=\cos \frac{\theta }{2}|0⟩+e^{j\varphi }\sin \frac{\theta }{2}|1⟩$$
然后根据这个角度，甚至可以把它画在球上（Bloch sphere），注意这种可视化与几何意义的向量完全没有关系

量子比特运算

了解意义之后，可以将其简化，设有复数 $a,b$，那么
$$\begin{gathered} |\psi ⟩=a|0⟩+b|1⟩=\left(\begin{array}{c}a\\ b\end{array}\right) \\ |0⟩=\left(\begin{array}{c}1\\ 0\end{array}\right),|1⟩=\left(\begin{array}{c}0\\ 1\end{array}\right) \end{gathered}$$
从此，关于量子比特的运算都可以使用线性代数的运算（加、减、数乘、矩阵乘法）

对于转置，需要注意转置的同时将复数共轭，
$$⟨\psi |=a^{\ast }⟨0|+b^{\ast }⟨1|$$
因为共轭之后有些好用的性质，如量子比特的点积

定义$|\psi ⟩=a_0|0⟩+a_1|1⟩,|\varphi ⟩=b_0|0⟩+b_1|1⟩$

点积为
$$⟨\psi |\varphi ⟩=\left(\begin{array}{cc}{a}_0^{\ast }& a_1^{\ast }\end{array}\right)\left(\begin{array}{c}{b}_0\\ b_1\end{array}\right)=a_0^{\ast }{b}_0+a_1^{\ast }{b}_0$$
于是就有性质
$$⟨\psi |\psi ⟩=a_0{a}_0^{\ast }+a_1{a}_1^{\ast }=|a_0{|}^2+|a_1{|}^2=1={\left||\psi ⟩\right|}^2$$

测量

由波函数的性质可以得来

测量$|\psi ⟩$处于状态$|x⟩$的概率为${\left|⟨x|\psi ⟩\right|}^2$，即$|\psi ⟩$在$|x⟩$方向上投影的模长平方

如可以计算出$|q_0\rangle= \tfrac{1}{\sqrt{2}}|0\rangle + \tfrac{i}{\sqrt{2}}|1\rangle \$的概率为各一半
$$\begin{array}{rl}|q_0⟩& =\frac{1}{\sqrt{2}}|0⟩+\frac{i}{\sqrt{2}}|1⟩\\ ⟨0|q_0⟩& =\frac{1}{\sqrt{2}}⟨0|0⟩+\frac{i}{\sqrt{2}}⟨0|1⟩\\ & =\frac{1}{\sqrt{2}}\cdot 1+\frac{i}{\sqrt{2}}\cdot 0\\ & =\frac{1}{\sqrt{2}}\\ |⟨0|q_0⟩{|}^2& =\frac{1}{2}\end{array}$$
将该向量画出来即为$x$轴，及如下公式 $\varphi =0,\theta =\frac{\pi }{2}$时
$$|\psi ⟩=\cos \frac{\theta }{2}|0⟩+e^{j\varphi }\sin \frac{\theta }{2}|1⟩$$

可以看出，$|\psi ⟩$到x轴y轴平面的投影，对x轴的夹角$\phi$即为相位，对实际$|0⟩,|1⟩$的概率没有影响

$|\psi ⟩$在这个球上几何向量到z轴的投影，到两端的距离，可以表示出该量子比特被观测到$|0⟩,|1⟩$的概率比值

（这个球上的投影，和测量时点积表示的投影，不是一个概念）

比如$x$轴投影到z轴后，到$|0⟩,|1⟩$的距离相等，于是观测时概率相等

如果$\theta =\frac{\pi }{3}$，则其投影到z轴为原点到$|0⟩$中点，概率比值为1：3，与计算相符。