第二章 机器学习(邱书)
通俗地讲机器学习ML就是让计算机从数据中进行自动学习得到某种知识或规律.作为一门学科机器学习通常指一类问题以及解决这类问题的方法即如何从观测数据样本中寻找规律并利用学习到的规律模型对未知或无法观测的数据进行预测。机器学习 ≈ 构建一个映射函数机器学习即如何从观测数据(样本)中寻找规律,并利用学习到的规律(模型)对未知或无法观测的数据进行预测。我们可以将一个标记好特征以及标签的芒果看作一个样本Sam
通俗地讲,机器学习(Machine Learning,ML)就是让计算机从数据中进行自动学习,得到某种知识(或规律).作为一门学科,机器学习通常指一类问题 以及解决这类问题的方法,即如何从观测数据(样本)中寻找规律,并利用学习 到的规律(模型)对未知或无法观测的数据进行预测。
机器学习 ≈ 构建一个映射函数
机器学习即如何从观测数据(样本)中寻找规律,并利用学习到的规律(模型)对未知或无法观测的数据进行预测。
我们可以将一个标记好特征以及标签的芒果看作一个样本(Sample),也经常称为示例(Instance). 一组样本构成的集合称为数据集(Data Set)。( 在很多领域,数据集也经常称为语料库(Corpus))。一般将数据集分为两部分:训练集和测试集.训练集(Training Set)中的样本是用来训练模型的,也叫训练样本(Training Sample),而测试集(Test Set)中的样本是用来检验模型好坏 的,也叫测试样本(Test Sample).我们通常用一个𝐷 维向量𝒙 = [𝑥1 , 𝑥2 , ⋯ , 𝑥𝐷] T 表示一个芒果的所有特征构成的向量,称为特征向量(Feature Vector),其中每一维表示一个特征. 并不是所有的样本特 征都是数值型,需要通 过转换表示为特征向 量。而芒果 的标签通常用标量𝑦来表示.
假设训练集 𝒟 由 𝑁 个样本组成,其中每个样本都是独立同分布的(Identically and Independently Distributed,IID),即独立地从相同的数据分布中抽取 的,记为
𝒟 = {(𝒙(1), 𝑦(1)), (𝒙(2), 𝑦(2)), ⋯ , (𝒙(𝑁), 𝑦(𝑁))}.给定训练集𝒟,我们希望让计算机从一个函数集合ℱ = {𝑓1 (𝒙), 𝑓2 (𝒙), ⋯}中自动寻找一个“最优”的函数𝑓 ∗ (𝒙) 来近似每个样本的特征向量 𝒙 和标签 𝑦 之间 的真实映射关系.对于一个样本𝒙,我们可以通过函数𝑓 ∗ (𝒙)来预测其标签的值𝑦 = 𝑓∗ (𝒙),或标签的条件概率𝑝(𝑦|𝒙) = 𝑓𝑦 ∗ (𝒙)如何寻找这个“最优”的函数 𝑓 ∗ (𝒙) 是机器学习的关键,一般需要通过学习算法(Learning Algorithm)𝒜 来完成. 在 有 些 文 献 中, 学 习算法也叫作学习器 (Learner). 这个寻找过程通常称为学习(Learning) 或训练(Training)过程. 这样,下次从市场上买芒果(测试样本)时,可以根据芒果的特征,使用学习 到的函数 𝑓 ∗ (𝒙) 来预测芒果的好坏.为了评价的公正性,我们还是独立同分布地 抽取一组芒果作为测试集 𝒟′,并在测试集中所有芒果上进行测试,计算预测结 果的准确率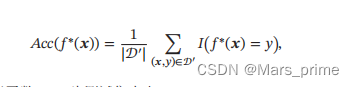 其中𝐼(⋅)为指示函数,|𝒟′ |为测试集大小.图给出了机器学习的基本流程.对一个预测任务,输入特征向量为 𝒙,输 出标签为𝑦,我们选择一个函数集合ℱ,通过学习算法𝒜和一组训练样本𝒟,从ℱ 中学习到函数𝑓 ∗ (𝒙).这样对新的输入𝒙,就可以用函数𝑓 ∗ (𝒙)进行预测.
其中𝐼(⋅)为指示函数,|𝒟′ |为测试集大小.图给出了机器学习的基本流程.对一个预测任务,输入特征向量为 𝒙,输 出标签为𝑦,我们选择一个函数集合ℱ,通过学习算法𝒜和一组训练样本𝒟,从ℱ 中学习到函数𝑓 ∗ (𝒙).这样对新的输入𝒙,就可以用函数𝑓 ∗ (𝒙)进行预测.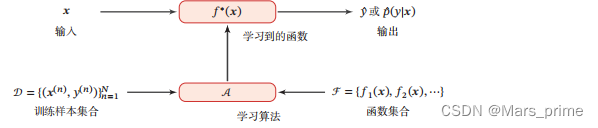
常见的学习类型
机器学习方法可以粗略地分为三个基本要素:模型、学习准则、优化算法.
模型:
输入空间 𝒳 和输出空间 𝒴 构成了一个样本空间.对于样本空间中的样本 样本的特征空间(𝒙, 𝑦) ∈ 𝒳 × 𝒴,假定 𝒙 和 𝑦 之间的关系可以通过一个未知的真实映射函数𝑦 =
𝑔(𝒙) 或真实条件概率分布𝑝𝑟 (𝑦|𝒙) 来描述.机器学习的目标是找到一个模型来近 映射函数𝑔 ∶ 𝒳 → 𝒴.似真实映射函数𝑔(𝒙)或真实条件概率分布𝑝𝑟 (𝑦|𝒙). 由于我们不知道真实的映射函数𝑔(𝒙)或条件概率分布𝑝𝑟 (𝑦|𝒙)的具体形式, 因而只能根据经验来假设一个函数集合ℱ,称为假设空间(Hypothesis Space), 然后通过观测其在训练集 𝒟 上的特性,从中选择一个理想的假设(Hypothesis) 𝑓 ∗ ∈ ℱ. 假设空间ℱ 通常为一个参数化的函数族 ℱ = {𝑓(𝒙; 𝜃)|𝜃 ∈ ℝ𝐷}, 其中𝑓(𝒙; 𝜃)是参数为𝜃 的函数,也称为模型(Model),
𝐷 为参数的数量.
常见的假设空间可以分为线性和非线性两种,对应的模型 𝑓 也分别称为线性模型和非线性模型.
线性模型
线性模型的假设空间为一个参数化的线性函数族,即
非线性模型
广义的非线性模型可以写为多个非线性基函数𝜙(𝒙)的线性组合
学习准则:
优化算法:
正则化:
模型选择
拟合能力强的模型一般复杂度会比较高,容易过拟合。
如果限制模型复杂度,降低拟合能力,可能会欠拟合。
偏差与方差分解
期望错误可以分解为

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容






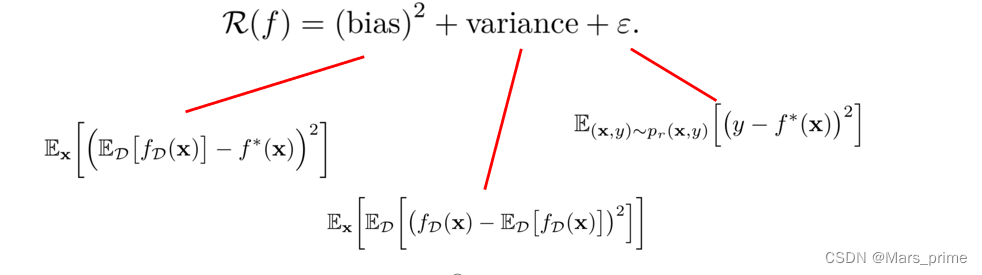







所有评论(0)