三种不同梯度下降方式对比

梯度下降

梯度下降是机器学习中一种非常重要的方法，每次通过计算损失函数loss的梯度，沿着其反方向，即损失函数loss下降最快的方向，进行更新参数，确保在短时间内能够得到较优的解，其公式如下所示：
$${\theta }_j={\theta }_j+\alpha \frac{\partial J(\theta )}{\partial {\theta }_j}$$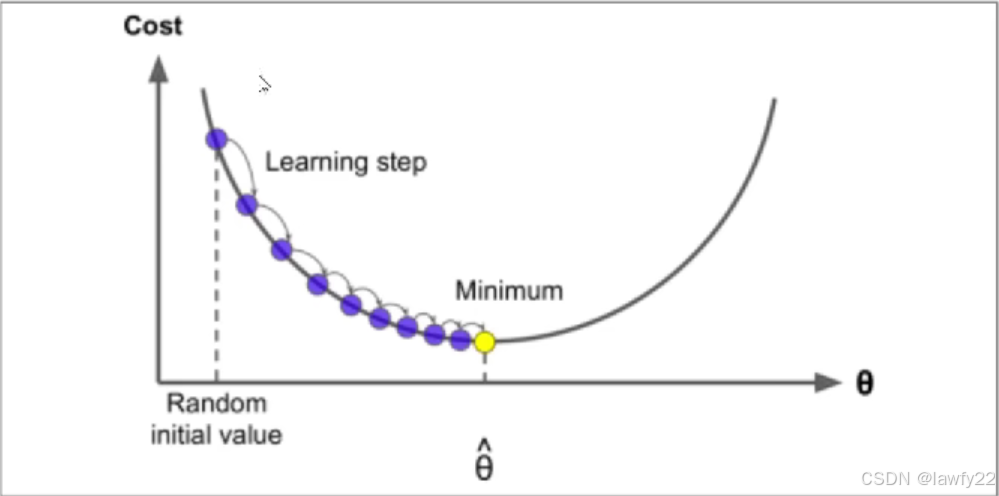

基本步骤：

• 找到合适的方向（计算梯度），沿着梯度的反方向去更新参数
• 选取适当的步长（学习率），不宜过大也不宜过小
• 按照方向和步长去更新我们的参数

其中，梯度下降大致又可以分为三种：

• 批量梯度下降
• 随机梯度下降
• 小批量随机梯度下降

本文从线性回归的基础上，探讨这三种梯度下降方式的区别

数据集的创建

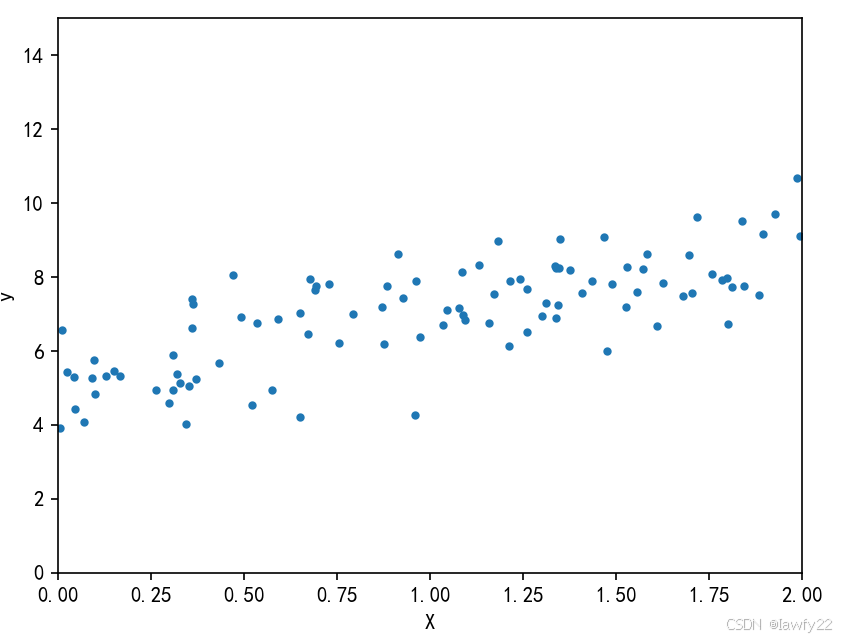
采用随机数，创建一维特征值，再根据线性方程式$y=5+2x$，创建对应的标签值

import numpy as np
import os
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

## 训练集
X = 2*np.random.rand(100, 1)
y = 5 + 2*X + np.random.randn(100, 1)  # 加上随机抖动
plt.plot(X, y, 'b.')
plt.xlabel('X')
plt.ylabel('y')
plt.axis([0, 2, 0, 15])
plt.show()

## 测试集
X_new = np.array([[0], [0.8], [1.1], [1.5], [2]])

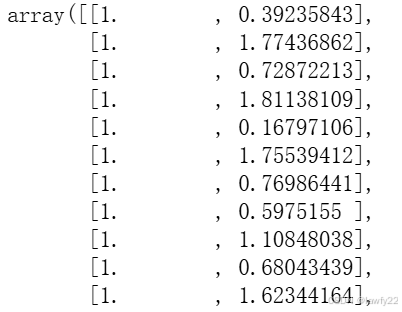
由于我们的模型是线性回归，存在偏置${\theta }_0$，因此还需要对数据进行预处理，即在数据前面加上一列的 $1$

从而使得X_b[0]对应的是我们的偏置项，X_b[1]对应的是权重项

X_b = np.c_[np.ones((100, 1)), X]  # 横向拼接
X_new_b = np.c_[np.ones((5, 1)), X_new]

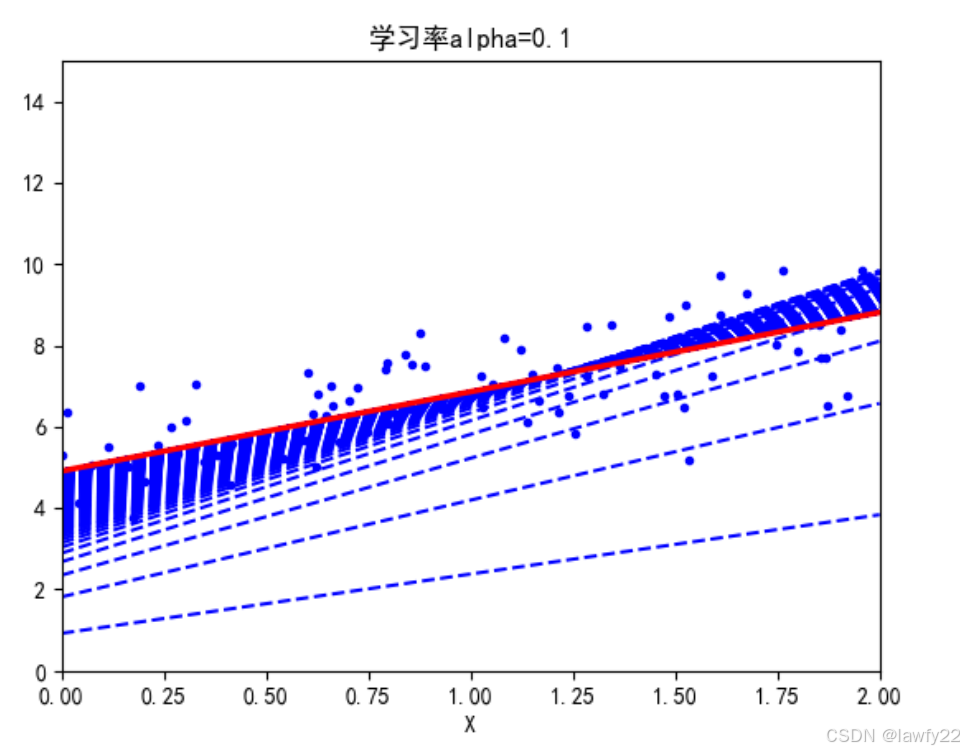
批量梯度下降

批量梯度下降就是每次更新梯度时，用所有样本去计算梯度
$${\theta }_j={\theta }_j+\alpha \frac{1}{m}\sum _{i=1}^m(y^i-h_{\theta }(x^i))x_j^i$$
优点：容易得到最优解

缺点：样本较大时，速度较慢

########## 批量随机梯度下降 ##########
theta_path_sgd = []
m = len(X_b)
num_iterations = 1000;
alpha = 0.1

def sgd(theta, num_iterations, alpha. theta_path):
    plt.plot(X, y, 'b.')  # 绘制数据原始图像
    for _ in range(num_iterations):
        if _ < num_iterations - 1 :
            y_pre = X_new_b.dot(theta)
            plt.plot(X_new, y_pre, 'b--')
        gradient = 2/m * X_b.dot(X_b.dot(theta)-y)
        theta = theta - alpha*gradient
        theta_path.append(theta)
    y_pre = X_new_b.dot(theta)
    plt.plot(X_new, y_pre, 'r--', linewidth=2.5)
## 批量梯度下降
theta = np.random.randn(2, 1)
sgd(theta, num_iterations, alpha, theta_path_sgd)

随机梯度下降

每次更新梯度时，只在总的样本中随机取出一个样本，进行梯度计算来更新参数
$${\theta }_j={\theta }_j+\alpha (y^i-h_{\theta }(x^i))x_j^i$$
优点：迭代速度较快

缺点：最终结果不一定收敛

往往在进行随机梯度下降时，迭代的次数较多

theta_path_bgd = []
m = len(X_b)
n_epochs = 50
theta = np.random.randn(2, 1)
t0 = 5
t1 = 50
plt.plot(X, y, 'b.')  # 画出原始图像
def learning_shcdule(t):
    return t0 / (t1 + t)  # 步长衰减率
for epoch in range(n_epoches):
    for i in range(m):
        if epoch = 0 and i < 20  # 只画出来部分迭代结果
        	y_pre = X_new_b.dot(theta)
            plt.plot(X_new, y_pre, 'b-', linewidth=1.5)
        # 随机选择一个样本
        random_index = np.random.randint(m)
        xi = X_b[random_index]
        yi = y[random_index]
        # 梯度计算
        gradient = 2*xi.T.dot(xi.dot(theta) - yi)
        alpha = learning(epoch*m + i)
        theta = theta - alpha*gradient
        theta_path_bgs.append(theta)
plt.plot(X_new, X_new_b.dot(theta), 'r-', linewidth=2.5)
plt.show()

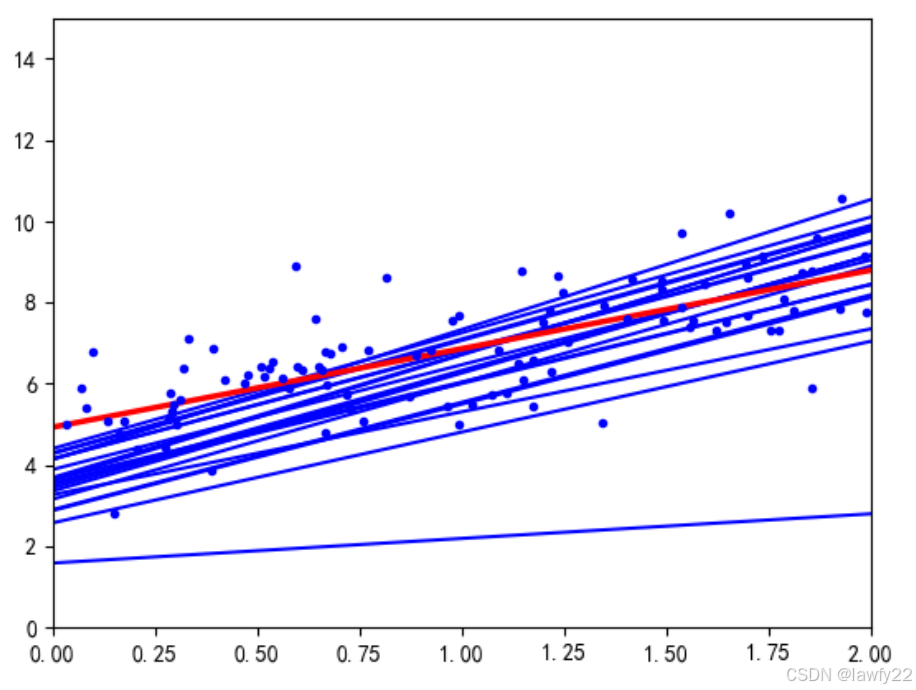
在随机梯度下降中，给学习率设置了一个衰减率。即在最初阶段，学习率较大，便于粗略地找到最优参数的大致范围，随着迭代的深入，学习率越来越小，细致寻找最优参数的精确范围

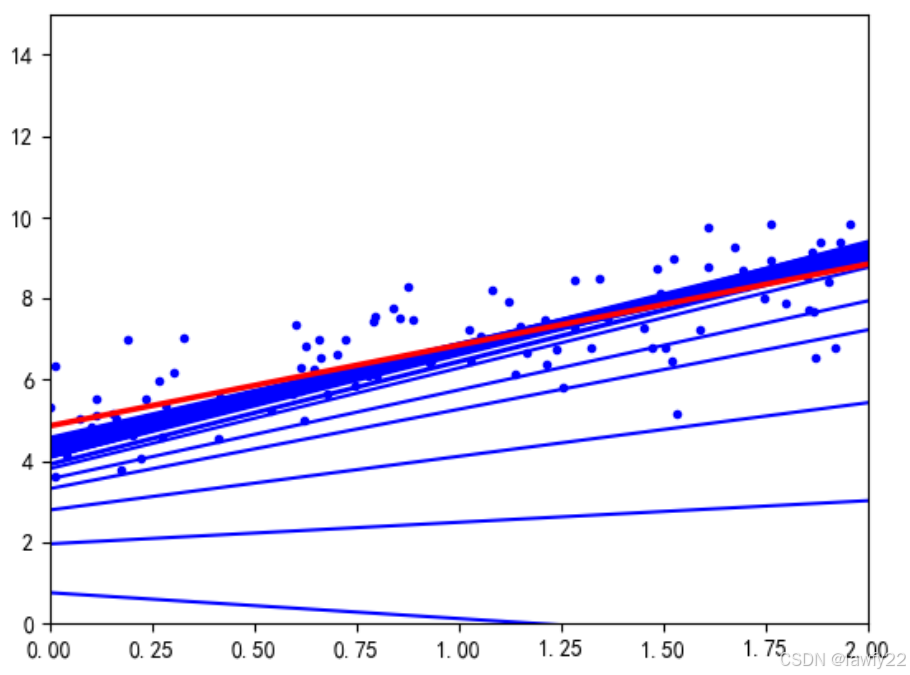
小批量随机梯度下降

这是上两种梯度下降方法的综合。

在每次迭代中，只在总的样本中随机选取部分样本，进行梯度计算，更新参数
$${\theta }_j={\theta }_j+\alpha \frac{1}{batch}\sum _{k=i}^{i+batch}(y^{(k)}-h_{\theta }(x^{(k)}))x_j^{(k)}$$
通常，小批量的个数用$batch$表示，且$batch$通常选取2的幂，如64，128，256…，便于计算机的计算

theta_path_mgd = []
min_batch = 16
theta = np.random.randn(2, 1)
n_epochs = 50

t = 0
for epoch in range(n_epochs):
    # 对数据进行洗牌操作，保证每次迭代拿到的批量数据是不一样的
    shuffled_index = np.random.permutation(m)
    X_b_shuffled = X_b[shuffled_index]
    y_shuffled = y[shuffled_index]
    for i in range(0, m, min_batch):
        t += 1  # 更新时间
         if t < 50:
            y_pre = X_new_b.dot(theta)
            plt.plot(X_new, y_pre, 'b-', linewidth=1.5)
        xi = X_b_shuffled[i: i+min_batch]
        yi = y_shuffled[i: i+min_batch]
        # 梯度计算
        gradient = 2/min_batch * xi.T.dot(xi.dot(theta)-yi)
        alpha = learning_schedule(t)  # 每一个epoch有m个数据 
        theta = theta - alpha*gradient
        theta_path_msgd.append(theta)
plt.plot(X_new, X_new_b.dot(theta), 'r-', linewidth=2.5)
plt.axis([0, 2, 0, 15])
plt.show()

三种梯度下降方法对比

图片摘自课程视频

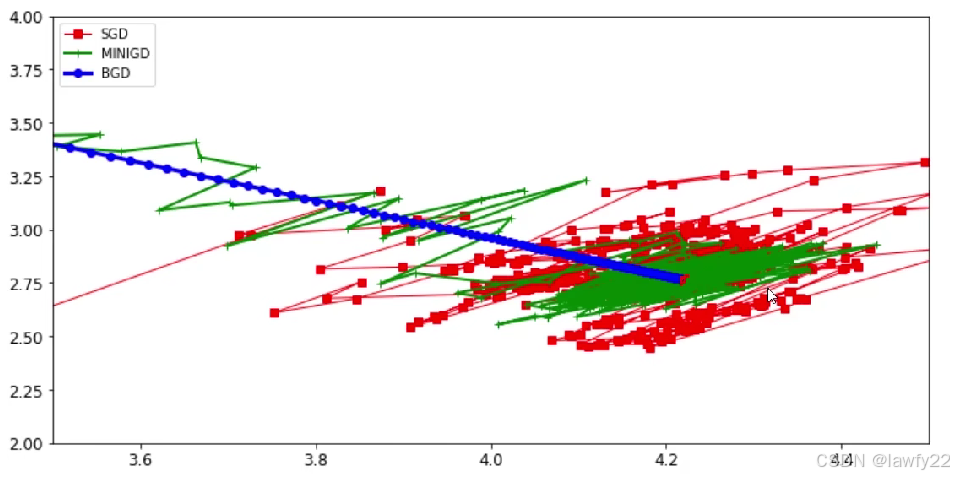
• 对批量梯度下降来说，由图可以看到，每一次迭代的方向都是正确的，从开始到结束，一直走到正确的道路方向
• 对于随机梯度下降来说，有图像可以观察到，在迭代的进行过程中，浮动偏离程度较大，但随着迭代次数的增加，最终还是能够收敛到最优参数值的地方
• 对于小批量随机梯度下降来说，虽然在迭代过程中有所浮动偏离，但浮动程度较随机梯度下降小，并且在很短的时间内，就收敛到了最优参数值附近