本文章的内容和知识为作者学习期间总结且部分内容借助AI理解，可能存在一定错误与误区，期待各位读者指正。
本文章中的部分例子仅用于生动解释相关概念，切勿结合实际过度解读。
语雀链接：《机器学习与深度学习》
部分内容来源：B站：李哥考研
本章内容已经更新完成，如有不足之处，不妨评论区一叙

  人工智能、机器学习、深度学习他们之间好像经常同时出现，其实他们是一种包含的关系

  机器学习是人工智能的核心技术手段，人工智能的目标是让机器能够像人一样智能地解决问题。而机器学习提供了一种让机器从数据中自动学习知识的方法来实现这一目标。
  深度学习是机器学习的一个分支，机器学习包含了很多不同的方法，如决策树、支持向量机等，深度学习是其中的一种特殊类型。
  我们可以借助AI来简单了解一下这三个名词的含义：

我想区分一下人工智能、机器学习、深度学习，你能举几个生动想象的例子为我介绍一下吗？

以下回答来自豆包：

人工智能（Artificial Intelligence AI）

想象人工智能是一个超级智能的城市。这个城市里有各种各样的智能设施和智能生物，它们可以完成各种各样复杂的任务。例如，智能安防系统，它就像城市的守护者。可以通过摄像头识别异常行为、分析人员流动等。它能够根据设定的安全规则，比如识别是否有人在禁区徘徊、是否发生了打斗等情况，并且及时发出警报，这体现了人工智能在视觉感知和决策方面的应用。

机器学习（Machine Learning ML）

把机器学习想象成一个学校。在这个学校里，学生（模型）通过不断地做练习题（数据）来学习知识。例如，一个预测天气的机器学习模型就像是气象学校里的一个勤奋学生。它会被输入大量过去的天气数据，包括温度、湿度、气压、风速等各种气象因素（这些数据就是练习题）。这个模型会根据这些数据，找到数据之间的规律，比如温度和湿度高的时候可能会下雨，气压变化与风向变化之间的关系等。随着数据量的增加，它学习的知识就越多，预测天气的准确性就可能越高。

深度学习（Deep Learning DL）

深度学习可以想象成一个超级复杂的神经网络迷宫。以图像识别为例，把一张猫的图片输入到深度学习模型中，就像是把一个小探险家（数据）放进了这个迷宫。这个迷宫有很多层（深度学习的多层神经网络），每层里有很多小房间（神经元）。在第一层，可能小探险家会先识别出一些简单的线条和颜色块，比如识别出猫的轮廓线条部分对应的颜色和形状。然后随着它在迷宫里深入（经过更多的层），它会逐渐组合这些简单的信息，识别出猫的眼睛、耳朵、尾巴等部分，最后在迷宫的出口（最后一层），它能够确定这是一张猫的图片。

机器学习算法简介：

  机器学习算法一般是基于数学，或者统计学的方法，具有很强的可解释性，例如KNN，决策树，朴素贝叶斯，这几个是经典的传统机器学习算法。听起来可能会有些枯燥，那接下来让我们简单感受一下这几个算法。

KNN：K最近邻居（K-Nearest Neighbors）

  今天月黑凤高，小圆寂寞难耐，想找小焰打一把王者荣耀，假设王者荣耀一共有三个段位，黄金、钻石、王者，小圆想根据小焰最近的匹配到的队友，来判断小焰是黄金还是钻石。

• 小焰最近100个队友，100个都是黄金段位
• 小焰最近200个队友，180个都是钻石段位
• 小焰最近200个队友，85个是黄金段位，95个是钻石段位
• 小焰最近200个队友，185个都是王者段位

  看了上面4种情况，你能根据KNN算法，来判断小焰是黄金还是钻石吗？前两种显然是很好判断的，由于对应段位队友所占比例相当大，我们很容易判断出情况1、2的结果分别是黄金和钻石段位。
  那么第三种情况下，两个段位所占比例相差无几，那么此时我们使用KNN算法就很难判断准确
  而第四种情况下，有些同学可能会认为小焰属于王者段位，那你掉入陷阱了，因为此时要求判断，小焰属于黄金还是钻石段位，王者段位的队友是无法作为判断依据的，所以你只能继续分析剩余15个队友，进而得出结果。

  KNN是一种监督学习算法，用于分类和回归问题。它的基本思想是通过测量不同数据点之间的距离来进行预测。KNN的工作原理可以概括为以下几个步骤：

1. 距离度量：KNN使用距离度量（通常是欧式距离）来衡量数据点之间的相似性
2. 确定邻居数量K
3. 投票机制

  如下图所示，我们使用多数表决的投票机制，也就是统计数量，当邻居数量K=3时，小焰被认为是黄金段位(黄色)，K=6时，被认为是钻石段位(蓝色)。同时我们也可以采用加权投票的方式，当K=3时，我们可以认为钻石段位离小焰更近，因此赋予其权重更高，从而可能得出小焰是钻石段位的结论。

决策树（Decision Tree）

小杏经常收到别人的邮件，但其中一部分是垃圾邮件，她根据这些邮件的特点和类型找到了一些规律

是否是认识的人	是否有垃圾关键词	是否是垃圾邮件
是	是	否
是	是	否
是	否	否
否	是	是
否	是	是
否	是	是
否	否	否
否	否	否

我们可以根据以往数据，构建出一个决策树，当新的数据进入时，通过二叉树进行预测类型

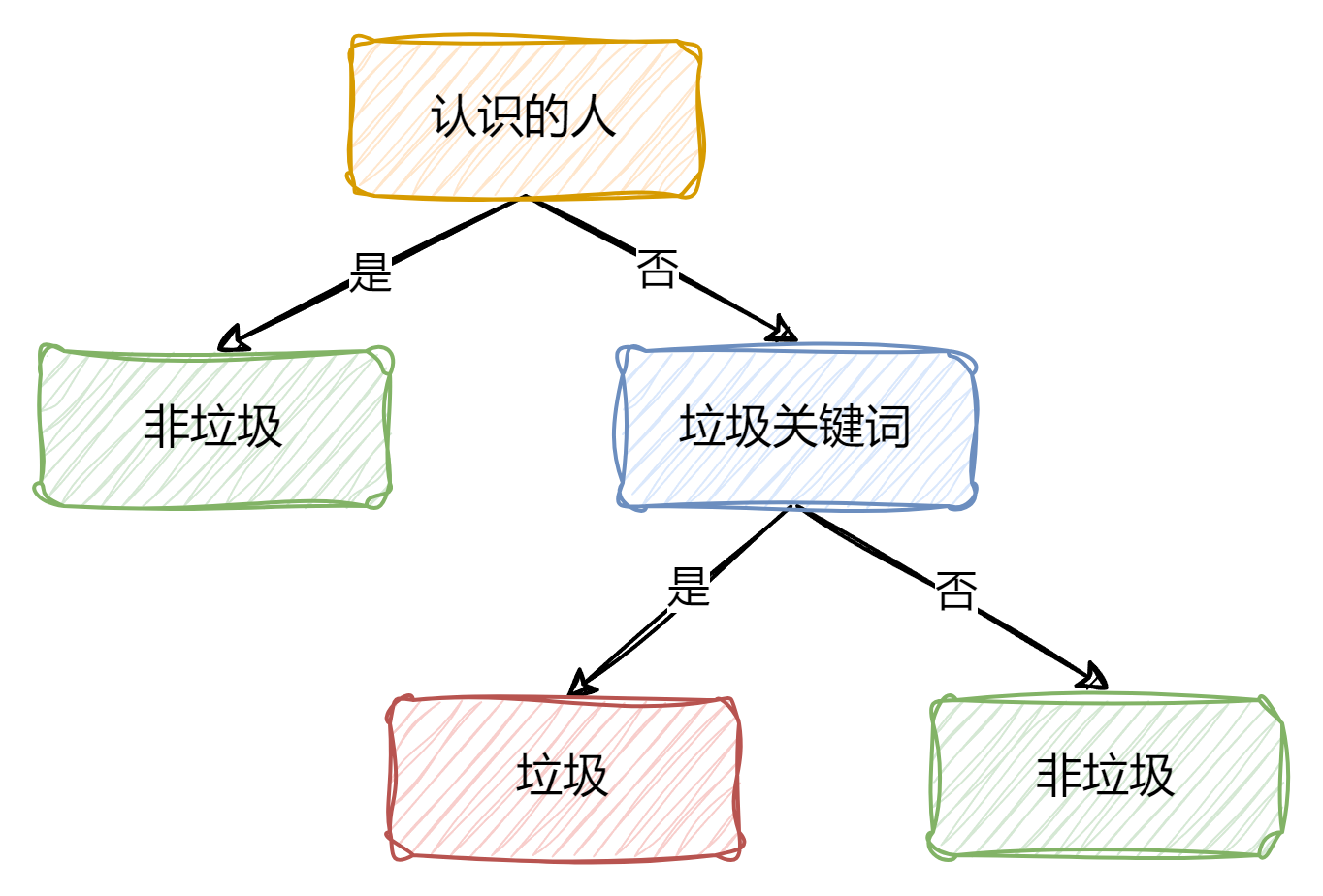
  决策树就像是一个树状的流程图，用于解决分类和回归问题。它从根节点开始，通过一系列的决策规则（内部节点），最终到达叶节点，叶节点代表了决策的结果。
  思考：如果出现了，一个没有垃圾关键词的邮件，但它确实是一封垃圾邮件，这一情况该怎么办？那么此时我们可以再添加一些其他特征（如是否存在链接等）来完善模型。这也暴露了决策树的一个缺点，就是决策树不善于处理未见过的特征 。

朴素贝叶斯算法（Naive Bayesian algorithm）

麻美学姐在玩攻略迷宫的游戏，现在一共有三个迷宫供她选择。

如果已知麻美学姐胜利通过迷宫，那么她选择迷宫A的概率是？
这种需要已知结果，反推过程的问题，我们需要用到朴素贝叶斯算法。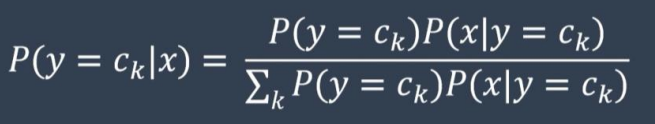

  将公式带入这个问题的话，也就是，选择迷宫A的概率=选择迷宫A且胜利的概率 / 胜利的概率
因此我们能得到选择迷宫A的概率= 0.20.2 / 0.20.2 + 0.60.6 +0.21 =0.066667
  机器学习具有数学上的可解释性，但准确性不是百分百，且不灵活，因此诞生了深度学习

深度学习简介

它基于人工神经网络，通过构建具有多个层次的神经网络模型来学习数据中的复杂模式。这些层次可以自动地从大量的数据中提取特征，从低级特征（如图像中的线条、边缘）逐步构建到高级特征（如物体的形状、纹理）。

简而言之就是设计一个很深的网络架构，让机器自己学。再简单一点，深度学习就是找一个函数F( )，实现从数据到结果的映射。

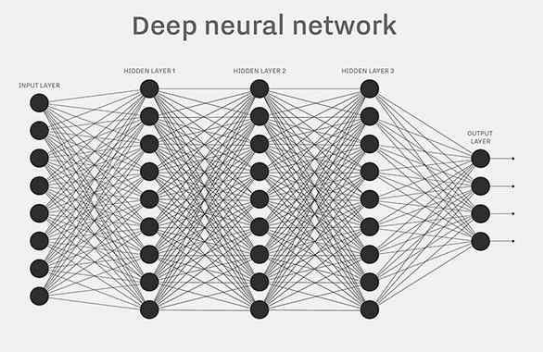
例如我们根据身高、体重、财富等因素推断一个人的寿命，或者根据一个动物的图片来判断这是哪个动物，甚至是根据一段描述来生成一个图片。由于这个函数F( )太过于复杂，因此我们需要机器自己学习。在F(X) = Y 中存在三个对象，函数F( ) ，输入X，输出Y，这三个是深度学习的基础。

常见的神经网络输入

常见的神经网络输入，一般有三种数据形式（并不严谨）

1. 向量： 例如 身高、体重、财富 （180, 150, 8000）
2. 矩阵/张量：图片，图片是由多个像素点构成，而每个像素点上不同的RGB值构成了不同颜色，因此一张图片可以由矩阵表示

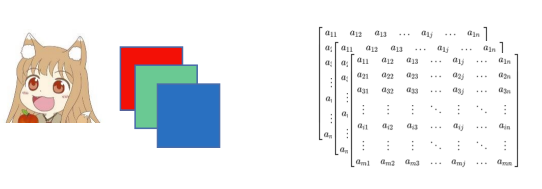
3. 序列：“你今天吃什么”，我用的"苹果"，我吃的"苹果"，这些输入需要一定的上下文或前后关系才能够理解，比如我们想知道这一段视频来自哪段电影，一段视频就属于序列输入。

常见的神经网络输出

我们想要的输出（任务类别）一般有以下几种

1. 回归任务（填空题）：根据以前的温度，来推测今天的温度有多高
2. 分类任务（选择题）：图片：猫/狗，疾病：轻度/中度/重度，结果具有一定的约束性
3. 生成任务（结构化）（简答题）：例如 ChatGPT，AI画图。其实生成任务也是通过分类实现，两者关系密切

  分类和回归是结构化的基础，分类时，是用数字来表示类别，有的时候需要多个模态的数据，比如图片，文字，声音。显然数据对于深度学习来说是重要的基础

回归与神经元

大家都说深度学习需要数据，这是为什么？因为我们需要大量的数据作为支撑，从而找到这个函数F( )，那么我们又应该如何从数据中找到想要的函数呢？

如何开始深度学习 待更新

让我们先从宏观方面了解一下

  我们先根据数据，大致定义一个函数，显然这个函数和实际的映射关系（函数）是有一定差距的，因此我们定义一个合适的损失函数，这个损失函数用来衡量我们定义的函数和实际结果之间存在的差距大小，然后我们根据差距对定义的函数进行优化，使得定义的函数逐渐接近实际的映射关系。

定义函数

  如何找一个函数呢？我们先根据数据(feature)和标签(label)进行一个简单分析

x	y
1	3.1
2	5.1
3	6.9
4	8.7
5	10.8
6	13.5
7	？

模型： (预测值) $y_0=wx+b$
上述模型是一个线性模型Linear model，w为权重weight，b为偏差bias，这两个都是未知参数。我们可以简单的给出一个预期函数$y_0=3x+2$

定义损失函数

接下来我们要定义一个损失函数Loss，这是一个有关w和b（未知参数）的二元函数，用于衡量模型预测结果与真实结果之间的差异程度。具体来说，如果我们选择了一组w，b，如果通过损失函数计算得出的结果很大，说明损失的多，也就是误差大，下面是一个计算单个损失结果的例子：

$$l(w,b)=|y_0-y|=|wx+b-y|$$

其中$y_0$为预测值，$y$为真实值，$w,b$为未知参数，由于实际情况下，未知参数数量很多，我们往往用${\theta }_i$来代替这些未知参数。

根据上面公式我们可以分析得出：当函数值越小，代表着偏差越小，说明我们定义的模型越符合实际，也就是误差越小，效果越好，反之则模型偏差大，效果差。我们可以用Loss来判断我们选择的这组参数(w和b)怎么样。

当然这只是其中一组数据的损失结果，而我们需要将所有数据的结果加和并求平均值。即

$$Loss:L=\frac{1}{N}\sum _{i=1}^{n}l$$

下面让我们举一些例子，我们根据6组数据，算出他们对应的损失，将其加和并平均，得出Loss=4.48

x	y（实际值）	y=3x+2(预测值)	loss
1	3.1	5	1.9
2	5.1	8	2.9
3	6.9	11	4.1
4	8.7	14	5.3
5	10.8	17	6.2
6	13.5	20	6.5
w =3 b =2 ,此时Loss = (1.9+2.9+4.1+5.3+6.2+6.5)/6 = 4.48

下面为两个常见的损失函数公式

均绝对误差 (Mean Absolute Error, MAE): $L(w,b)=\frac{1}{n}{\sum }_{i=1}^n|y_0-y|$

均方误差 （Mean Squared Error, MSE): $L(w,b)=\frac{1}{n}{\sum }_{i=1}^n(y_0-y{)}^2$

模型优化

  由于Loss函数表示了预测结果与真实结果之间的差异程度,因此我们应该尽可能找到一组$w$和$b$使得Loss的结果最小，这也才能尽可能与真实结果接近。所以我们需要根据之前的Loss结果来进一步优化我们之前选取的$w$和$b$。
$$w^{\ast },b^{\ast }=arg\underset{w,b}{\min }L$$
  $w^{\ast },b^{\ast }$表示最优的权重和偏差，这些值是通过最小化损失函数$L$得到的。也就是说，在所有可能的权重和偏差组合中, $w^{\ast }$和$b^{\ast }$是使损失函数 达到最小值的那组w和b。

我们采用梯度下降的方法，来对未知参数进行优化（找到最优的权重和偏差）。

梯度下降（Gradient Descent）是一种优化算法，用于最小化一个函数（如机器学习中的损失函数）。其基本思想是沿着函数的梯度（导数）的反方向逐步更新模型的参数，使得函数值（损失值）不断下降，最终找到函数的最小值（或局部最小值）。

具体步骤如下：

1. 随机选择一个$w^0$（参数b同理）
2. 计算$\frac{\partial L}{\partial w}{|}_{w=w^0}$
3. 更新w的值 $w^1=w^0-\eta \frac{\partial L}{\partial w}{|}_{w=w^0,b=b^0}$

我们尝试理解一下上面的步骤：
  第一步很好理解，不必多言。
  第二步，$L$对$w$求偏导，并求在$w_0$点处的值，学过高等数学的同学会很好理解，其目的就是为了观察，当$w$变化时，$L$是如何变化的，如果当此时偏导值大于0，就说明随着$w$的增大，$L$的值也会增大，此时我们应该将$w$减小，以保证$L$的值减小。这为我们进一步优化$w$提供了方向。
  第三步，根据上一步求出的偏导值，对$w$进行优化，此时并没有简单地加减，而是引入了一个变量$\eta$，$\eta$称之为学习率（learning rate）是一个超参数，这是一个人为规定的参数它决定了在每次迭代中，模型参数沿着梯度方向更新的步长大小，如果学习率过大，模型参数在更新时会 “跨” 过损失函数的最小值点，导致算法无法收敛，甚至可能使损失函数值越来越大。因此选用一个合适的$\eta$，对于模型优化是很重要的，当然这些都是后话了。

步长过大，反而偏离实际值

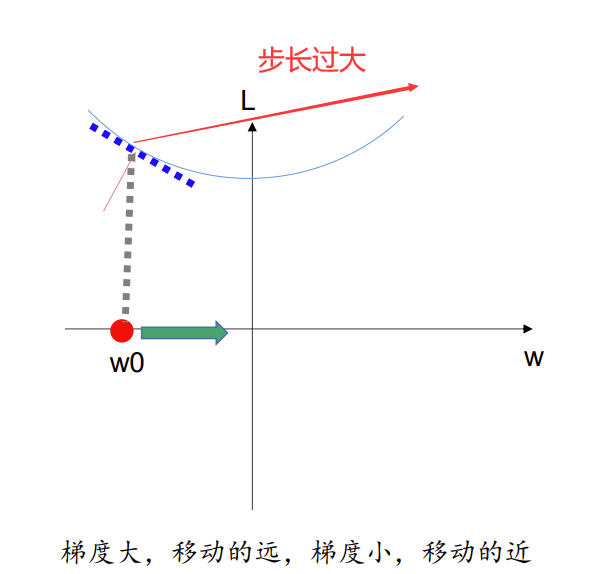
显然这些步骤并不需要我们手动去算，只需要理解原理，之后可以借助torch框架进行自动计算。