一.对数几率回归的定义

1.1 广义线性模型

在之前的机器学习(一)：深入解析线性回归模型一文中所介绍的线性模型都是基于$y=w^{T}x+b$这种形式的。但对于某些数据集虽然其自变量$x$与因变量$y$并不满足一元函数关系，但是可以通过某些函数$g(.)$让输入空间$x$到输出空间$y$的非线性函数映射转换成输入空间$x$到输出空间$g(y)$的线性函数映射，即：
$$y=g^{-1}(w^{T}x+b)$$
其中，$g(.)$为单调可微函数。为了方便理解这里也给出一个例子：当$y$在指数尺度上变化时，我们可以让$lny$作为线性模型逼近的目标，即$lny=w^{T}x+b$，这就是所谓的对数线性回归，其对应的示意图如下：

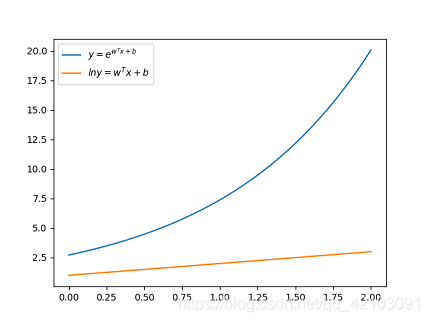
可知在上述例子中$ln(.)$函数即为$g(.)$ ，它起到了将线性回归模型的预测值与真实标记联系起来的作用。

1.2 对数几率回归的概念

线性回归模型帮助我们用最简单的线性方程实现了对数据的拟合，然而，这只能完成回归任务，无法完成分类任务，若要做分类任务则可以通过寻找一个单调可微函数$g(.)$将分类任务的真实标记$y$与线性回归模型的预测值联系起来。以二分类任务为例，其输出标记 y ∈ { 0 , 1 } y \in \lbrace 0,1 \rbrace y∈{0,1}，而线性回归模型产生的预测值$z=w^{T}x+b$是实值，因此需要将实值$z$转换为0/1值，而对数几率函数$y=\frac{1}{1+e^{-z}}$正是这样一个符合条件的单调可微函数，其图像如下所示：

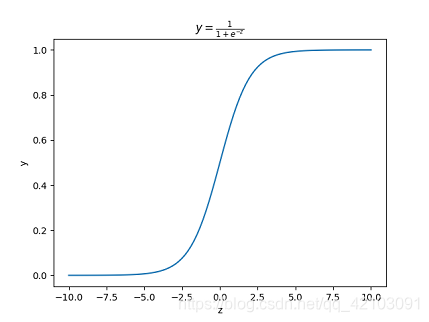
可知对数几率函数将$z$值转化为一个接近0或1的$y$值，并且其输出在$z=0$附近变化很陡。将$z=w^{T}x+b$带入对数几率函数$y=\frac{1}{1+e^{-z}}$可得：
$$y=\frac{1}{1+e^{-(w^{T}x+b)}}$$
将$y$看作样本$x$作为正例的概率，$1-y$是其为反例的概率，两者的比值$\frac{y}{1-y}=\frac{1}{e^{-(w^{T}x+b)}}=e^{-(w^{T}x+b)}$称为几率，几率反映了$x$作为正例的相对可能性，对几率取对数得到对数几率如下：
$$ln\frac{y}{1-y}=w^{T}x+b$$
可知上述公式实际上是使用线性回归模型的预测结果逼近真实标记的对数几率，因此该模型被称为对数几率回归（logistic regression）。由对数几率回归模型可知，当$y>1-y$时，则$\frac{y}{1-y}>1$，$ln\frac{y}{1-y}>0$；当$y<1-y$时，则$\frac{y}{1-y}<1$，$ln\frac{y}{1-y}<0$。因此对数几率大于0时判为正例，当对数几率小于0时判为反例，否则可以任意判别。

二.模型参数确定

2.1 极大似然估计

先举个栗子吧：猎人师傅和徒弟一同去打猎，遇到一只兔子，师傅和徒弟同时放枪，兔子被击中一枪，那么是师傅打中的，还是徒弟打中的？显然一般我们都会猜测是师傅打中的，因为师傅的枪法一般高于徒弟。而这样猜测是基于一个理论：概率最大的事件，最可能发生，这其中体现的就是极大似然估计的数学思想。通俗来理解，极大似然估计就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！

这里从数学上再给出一个例子：设一批产品中有合格品和不合格品，我们现在需要计算一批产品的不合格品率$p$。从中任取一个产品，用随机变量$X$表示其合格与否，$X=0$表示该产品是合格品，$X=1$表示该产品是不合格品，则$X$服从两点分布$B(1,p)$，现随机选取$n$个产品$X_1,X_2,...,X_n$检查其是否合格，得到样本的观测值$x_1,x_2,...,x_n$，其概率为：
P { X 1 = x 1 , X 2 = x 2 , . . . , X n = x n } = ∏ i = 1 n p x i ( 1 − p ) 1 − x i = p ∑ i = 1 n x i ( 1 − p ) n − ∑ i = 1 n x i P\lbrace X_1=x_1,X_2=x_2,...,Xn=x_n \rbrace=\prod_{i=1}^n p^{x_i}(1-p)^{1-x_i}=p^{\sum_{i=1}^nx_i}(1-p)^{n-\sum_{i=1}^nx_i} P{X1​=x1​,X2​=x2​,...,Xn=xn​}=i=1∏n​pxi​(1−p)1−xi​=p∑i=1n​xi​(1−p)n−∑i=1n​xi​
在这个例子中，我们已知的是一组$n$个产品的观测值$x_1,x_2,...,x_n$，未知的是不合格品率$p$，那么我们如何选择参数$p$呢，根据概率最大的事件最可能发生的思想，我们只需要找到使得上述概率$P$最大所对应的$p$即可。

2.2 $w$和$b$的确定

前面提过可以把$y$理解为一个样本是正例的概率，把$1-y$理解为一个样本是反例的概率，若将$y$和$1-y$分别视为类后验概率估计$p(y=1|x)$和$p(y=0|x)$，则显然有：
$$\begin{gathered} p(y=1|x)=\frac{1}{1+e^{-(w^{T}x+b)}}=\frac{e^{w^{T}x+b}}{1+e^{(}{w}^{T}x+b)} \\ p(y=0|x)=1-P(y=1|x)=\frac{1}{1+e^{w^{T}x+b}} \end{gathered}$$
假设给定的数据集为 D = { ( x i , y i ) } ( i ∈ [ 1 , m ] ) D=\lbrace (x_i,y_i) \rbrace (i \in [1,m]) D={(xi​,yi​)}(i∈[1,m])，再用$p(yi|xi;w,b)$表示参数为$w$和$b$下，已知自变量为$x_i$，而预测值为$y_i$的概率，则根据极大似然估计法我们可以得出：
$$P=\prod _{i=1}^{m}p(yi|xi;w,b)$$
但是由于预测概率都是小于1的，如果直接对所有样本的预测概率求积，所得的数会非常小，当样例数较多时，会超出精度限制。所以，一般来说会对概率取对数，得到对数似然$\ell (w,b)$，此时求所有样本的预测概率之积就变成了求所有样本的对数似然之和，即：
$$\ell (w,b)=\sum _{i=1}^{m}ln(p(yi|xi;w,b))$$
而我们的目标就是最大化对数似然$\ell (w,b)$，此时的$w$和$b$就是我们的最优解。参考周志华的《机器学习》中的表示，我们令$\beta =(w;b)$，$\hat{x}=(x;1)$，则$w^{T}x+b$可表示为${\beta }^T\hat{x}$，再令$p_1(\hat{x};\beta )=p(y=1|\hat{x};\beta )$，$p_0(\hat{x};\beta )=p(y=0|\hat{x};\beta )=1-p_1(\hat{x};\beta )$，则$\ell (w,b)$可以重写为：
$$\begin{array}{rl}\ell (w,b)=\ell (\beta )& =\sum _{i=1}^{m}ln(y_i{p}_1(\widehat{x_i};\beta )+(1-y_i)p_0(\widehat{x_i};\beta ))\\ & =\sum _{i=1}^{m}ln(\frac{y_i{e}^{{\beta }^T{\hat{x}}_i}}{1+e^{{\beta }^T{\hat{x}}_i}}+\frac{1-y_i}{1+e^{{\beta }^T{\hat{x}}_i}})\\ & =\sum _{i=1}^m(ln(y_i{e}^{{\beta }^T{\hat{x}}_i}+1-y_i)-ln(1+e^{{\beta }^T{\hat{x}}_i}))\end{array}$$
考虑到 y i ∈ { 0 , 1 } y_i \in \lbrace 0,1 \rbrace yi​∈{0,1}可得：

• 当$y_i=0$时，$\ell (\beta )=-ln(1+e^{{\beta }^T{\hat{x}}_i})$
• 当$y_i=1时$，$\ell (\beta )={\beta }^T{\hat{x}}_i-ln(1+e^{{\beta }^T{\hat{x}}_i})$

综上可得，只要在$y_i=1$时所对应的公式中的${\beta }^T{\hat{x}}_i$项前加上$y_i$就可以合并以上两种情况了，即：
$$\ell (\beta )=\sum _{i=1}^m(y_i{\beta }^T{\hat{x}}_i-ln(1+e^{{\beta }^T{\hat{x}}_i}))$$
但是为了能够求解，我们将$\ell (\beta )$的最大值转换成了求解$-\ell (\beta )$最小值，即：
$$\ell (\beta )=\sum _{i=1}^m(-y_i{\beta }^T{\hat{x}}_i+ln(1+e^{{\beta }^T{\hat{x}}_i}))$$

之所以要这样转换是因为$-\ell (\beta )$是高阶连续凸函数，它可以通过数值优化算法来求得最优解，常见的数值优化算法有梯度下降法，关于梯度下降这里推荐一篇超级好的博客——深入浅出–梯度下降法及其实现。

根据梯度下降法，首先需要对$\ell (\beta )$求导，其对应的结果如下：
$$\begin{array}{rl}\frac{\partial \ell (\beta )}{\partial \beta }& =\sum _{i=1}^m-y_i{\hat{x}}_i+\frac{e^{{\beta }^T{\hat{x}}_i}}{1+e^{{\beta }^T{\hat{x}}_i}}{\hat{x}}_i\\ & =-\sum _{i=1}^m{\hat{x}}_i(y_i-p_1({\hat{x}}_i;\beta ))\end{array}$$
则参数更新过程中，第$t+1$轮迭代的更新公式为：
$${\beta }^{t+1}={\beta }^t-lr\times \frac{\partial \ell (\beta )}{\partial \beta }$$
其中$lr$为学习率。

三.模型实现

3.1 数据集的生成

首先通过numpy随机生成了一个数据集，数据集中包含1000个点，点分为两大类 { 0 , 1 } \lbrace 0,1 \rbrace {0,1}，每类各包含500个点，数据集展示如下：

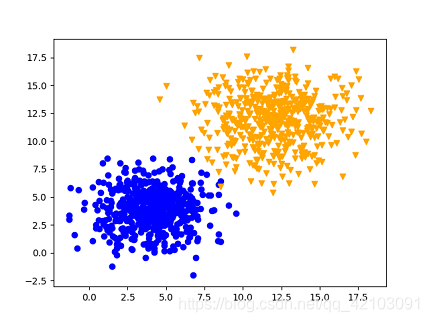
对应的数据集生成源码如下：

def generateDataset(train_rate=0.7,size=1000):
    """
    功能：生成数据集并按7:3划分训练集和测试集
    train_rate：训练集所占比例，剩下的即为测试集
    size：数据集大小
    """
    #两种标签的数据量各占一半
    label_size = size // 2

    #标签为0的数据点生成
    x11 = np.random.normal(4,1.8,label_size).reshape(-1,1)
    x12 = np.random.normal(4,1.8,label_size).reshape(-1,1)
    y1 = np.zeros(shape=(label_size,1))

    #标签为1的数据集点生成
    x21 = np.random.normal(12,2.3,label_size).reshape(-1,1)
    x22 = np.random.normal(12,2.3,label_size).reshape(-1,1)
    y2 = np.ones(shape=(label_size,1))

    #合并成完整的数据集
    x1 = np.vstack((x11,x21))
    x2 = np.vstack((x12,x22))
    ones = np.ones(shape=(size,1))
    x = np.hstack((x1,x2,ones))
    y = np.vstack((y1,y2))
	
    #输出两类标签的横纵坐标，是为了后面可视化展示方便
    return (x11,x12,x21,x22),x,y

3.2 对数几率回归模型实现

我们的目标是寻找一条直线$w_{1}x+w_{2}y+b=0$，使得其刚好能够将上述两种标签的点分割开来，参照第二节的介绍对数几率回归实现如下，为了方便理解，这里给出一些参数说明：其中beta表示$\beta$，beta_x表示${\beta }^T{\hat{x}}_i$，lbeta表示$\ell (\beta )$，dbeta表示$\frac{\partial \ell (\beta )}{\partial \beta }$：

import numpy as np
from numpy import linalg
from data import generateDataset,spiltDataset
import matplotlib.pyplot as plt

def initializeBeta(feature_nums):
    """
    功能：初始化参数Beta=(w;b)
    """
    beta = np.zeros(shape=(feature_nums,1))
    beta[-1] = 1
    return beta

def train(train_x,train_y,iterations=100,learning_rate=0.001):
    """
    功能：模型训练
    train_x,train_y：训练数据特征集，训练数据标签集
    iterations：迭代次数
    learning_rate
    """
    train_x,train_y = train_x.T,train_y.reshape(-1)
    #初始化beta参数
    beta = initializeBeta(train_x.shape[0])
    #开始训练
    for i in range(iterations):
        #beta与xi相乘
        beta_x = np.dot(beta.T[0], train_x)
        #计算l(beta)
        lbeta = np.sum(-1 * train_y*beta_x + np.log(1 + np.exp(beta_x)))
        #l(beta)对beta求偏导
        dbeta = np.dot(train_x,-1*train_y + np.divide(np.exp(beta_x),1+np.exp(beta_x))).reshape(-1,1)
        #更新beta
        beta -= dbeta*learning_rate

        #print('iteraing {} times lbeta is {}'.format(i + 1,lbeta))

    return beta

def test(test_x,test_y,beta):
    """
    功能：计算测似集的准确率
    test_x,test_y：测试数据特征集，测试数据标签集
    """
    #计算出预测值
    pred_y = np.dot(beta.T[0],test_x)
    #预测值y>0则为正例1，否则为反例0
    pred_y[pred_y >= 0] = 1
    pred_y[pred_y < 0] = 0
    #计算预测的准确率
    bingo = 0
    for i,yi in enumerate(pred_y):
        if yi == test_y[i]:#预测正确
            bingo += 1
    #print(bingo,test_y.shape[0])
    return bingo / test_y.shape[0]

if __name__ == "__main__":
    #生成数据集
    points,x,y = generateDataset()
    #划分训练集与测试集
    train_x,test_x,train_y,test_y = spiltDataset(x,y)
    #训练并获得超级参数
    beta = train(train_x,train_y)
    print(beta)
    test_x,test_y = test_x.T,test_y.reshape(-1)
    #测试模型在测试集上的准确率
    acc = test(test_x,test_y,beta)
    print('the acc of test dataset is {}'.format(acc))
    x11,x12,x21,x22 = points
    plt.scatter(x11,x12,c='b',marker='o')
    plt.scatter(x21,x22,c='orange',marker='v')
    x3 = np.random.randint(0,15,size=1000)
    w1,w2,b = beta[0][0],beta[1][0],beta[2][0]
    #w1x11 + w2x12 + b = 0即为我们要找的直线，且x12实际上就是y
    y3 = -1*(w1*x3 + b) / w2
    plt.plot(x3,y3,c='r')
    plt.show()

上述代码的运行结果如下图所示，其中红色的线即为我们所求的直线$w_{1}x+w_{2}y+b=0$：

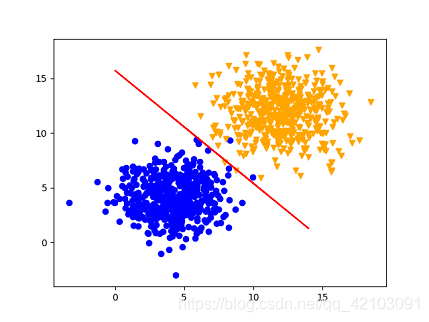
四.参考文献

• 对数几率回归 —— Logistic Regression
• 一文搞懂极大似然估计
• 对数几率回归（西瓜书公式推导）
• 用对数几率回归实现周志华《机器学习》习题3.3西瓜分类，python编程
• 《机器学习》——周志华

以上便是本文的全部内容，要是觉得不错的话，可以点个赞或关注一下博主，后续还会持续带来各种干货，当然要是有问题的话也请批评指正！！！