机器学习——决策树(Decision Trees)
决策树是机器学习中一种最为常见的算法。顾名思义,决策树是基于树结构来进行决策的,这恰是人类在面对决策问题时一种很自然的处理机制。决策树的生成算法可以说是信息论的一种应用,但它其实只用到了信息论中的一小部分思想。因此对信息论有个基础性的理解时很有必要的。
决策树
决策树是机器学习中一种最为常见的算法。顾名思义,决策树是基于树结构来进行决策的,这恰是人类在面对决策问题时一种很自然的处理机制。决策树的生成算法可以说是信息论的一种应用,但它其实只用到了信息论中的一小部分思想。因此对信息论有个基础性的理解时很有必要的。
基本原理
1、信息论
1.1 信息论简介
信息论创始人克劳德·埃尔伍德·香农被公认为是二十世纪最聪明的人之一。他在1948年发表的划时代的论文——“通讯的数学原理”奠定了现代信息论的基础。
信息论主要内容可类比语言来阐述,通常具有以下两个重要特点。
- 最常用的词汇(如:“的”、“好”、“行”)应该要比相对而言不太常用的词(如“自行车”、“宇宙”、“地球”)更短一些。
- 如果句子的某一部分被漏听或者由于噪声干扰(比如身处闹市)而被误听,听者应该仍可以抓住句子的大概意思。该特点也被称为“鲁棒性(Robustness)”。
需要注意的一点是,信息论不会考虑一段消息的重要性或内在意义,比如像“救命”这样的话显然比“你好”这样的话更重要也更有意义,而信息论只会关注信息量和可读性方面的问题。
既然关注的是信息量,就需要定义一种信息量的度量方法。决策树生成算法背后的思想正是利用该度量方法衡量一种数据划分的优劣,从而生成一个“判定序列”。具体而言,它会不断寻找最优的数据划分,使得在该划分下获得的信息量最大。这也正是决策树的精髓所在。
1.2 不确定性
在决策树的生成中,获得信息量的度量方法是从反方向来定义的:若一种划分使得“不确定性”减少的越多,即意味着该划分获取的信息信息就越多。至此,关键问题就在于如何度量数据的不确定性(或说不纯度Impure)。常见的信息量度量标准有两个:信息熵(Entropy)和基尼系数(Gini index)。
1.2.1 信息熵
信息熵基本公式为: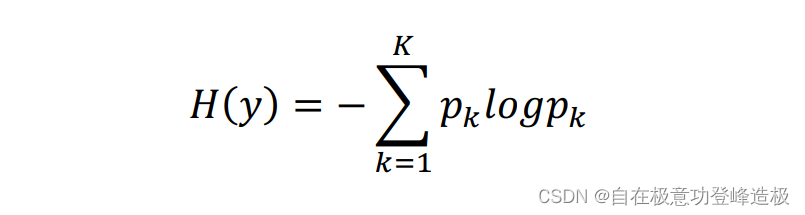
在实际使用中经常采用经验熵来估计信息熵(其思想也就是“频率估计概率”):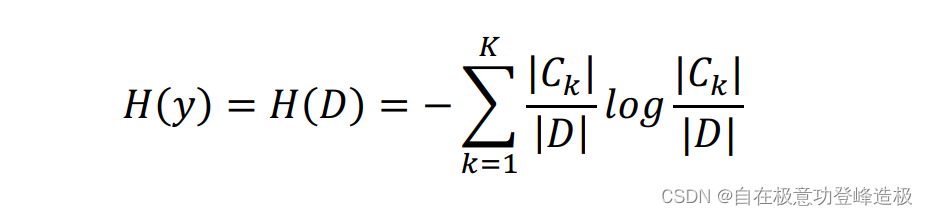
上式假设随机变量yyy的取值空间为c1,c2,…,ck{c_1,c_2,…,c_k}c1,c2,…,ck,pkp_kpk表示yyy取
ckc_kck的概率:pk=p(y=ck)p_k=p(y=c_k)pk=p(y=ck),∣Ck∣|C_k |∣Ck∣代表随机变量yyy中类别为ckc_kck的个数,∣D∣|D|∣D∣代表DDD的总样本个数。
一般而言,公式中对数的底会取为2,此时信息熵H(y)的单位叫做比特(bit);如果把底数取为e(即取自然对数)的话,H(y)H(y)H(y)的单位就叫做纳特(nat)
那么上述公式是如何来度量不确定性的?可以证明当以下条件成立时: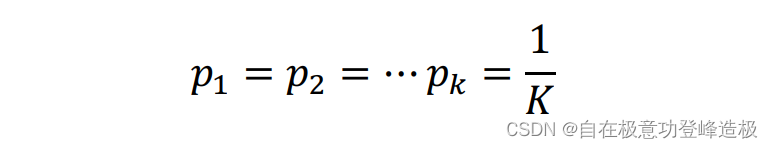
H(y)H(y)H(y)达到最大值−log1/K-log 1/K−log1/K、亦即logKlogKlogK。由于pk=(y=ck)p_k=(y=c_k)pk=(y=ck),上式意味着随机变量yyy取每一个类的概率是相同的,亦即yyy完全没有规律可循,若像预测它的取值只能靠运气。而我们的目的是让y的不确定性减小、亦即让yyy变得有规律可循,以方便我们预测。严格来说,就是yyy取某个类的概率特别大,取其他类的概率特别小。极端的例子自然就是存在某个k∗k^*k∗,使得p(y=c(k∗))=1p(y=c_{(k^* )} )=1p(y=c(k∗))=1、p(y=ck)=0p(y=c_k )=0p(y=ck)=0,∀k≠k∗∀k≠k^*∀k=k∗,亦即yyy生成的样本总属于c(k∗)c_(k^* )c(k∗)类。带入H(y)H(y)H(y)的定义式,可以发现此时H(y)=0H(y)=0H(y)=0,亦即yyy生成的样本没有不确定性。
接下来举个二分类的例子,加深一下对于信息熵的理解。即K=2K=2K=2时。不妨先假设yyy只取0、1二值,再设: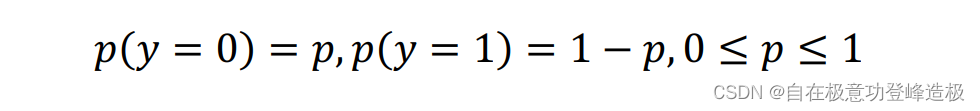
那么此时的信息熵: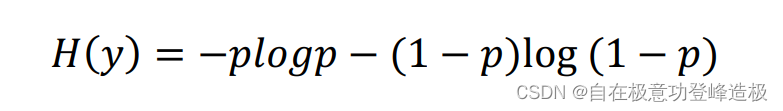
由此可以得到H(y)H(y)H(y)随ppp变化的函数曲线如下图所示(这里对数取底数为2)。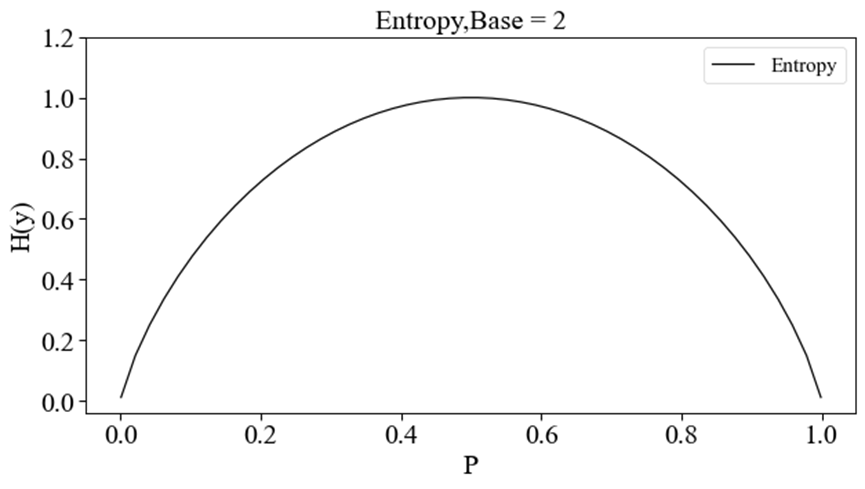
该图说明:随着这两类样本的分离的难易程度(ppp与1−p1-p1−p越接近越不容易分离,亦即p=0.5p=0.5p=0.5时H(y)H(y)H(y)达到最大),信息熵H(y)H(y)H(y)呈现先增加后减少的变化趋势。
以上的叙述说明,yyy越乱意味着H(y)H(y)H(y)越大,yyy越有规律意味着H(y)H(y)H(y)越小,亦即H(y)H(y)H(y)确实是可以作为不确定性的度量标准,从而可以作为信息的度量方法。
1.2.2 基尼系数
基尼系数基本公式为: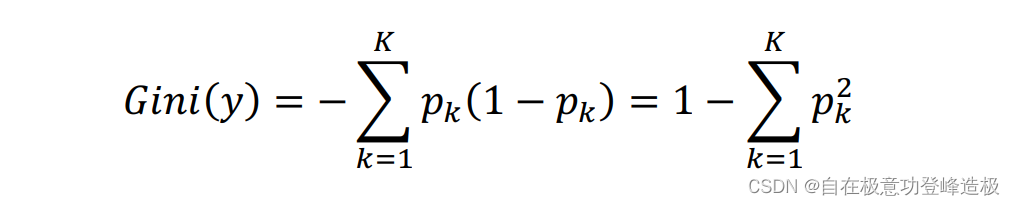
在实际使用中经常采用经验基尼系数来进行估计: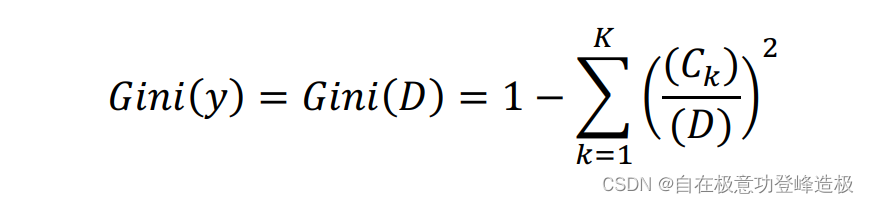
与信息熵类型,同样可以证明,当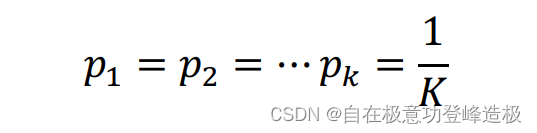
是,Gini(y)Gini(y)Gini(y)取得最大值1−1/K1-1/K1−1/K;当存在k∗k^*k∗使得k∗=1k^*=1k∗=1、Gini(y)=0Gini(y)=0Gini(y)=0。
这里再次以上述二分类为例子,即当K=2K=2K=2时可以导出: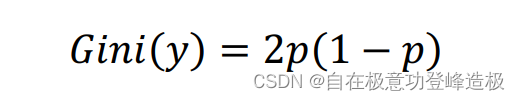
此时Gini(y)Gini(y)Gini(y)随ppp变化的函数曲线如下图所示。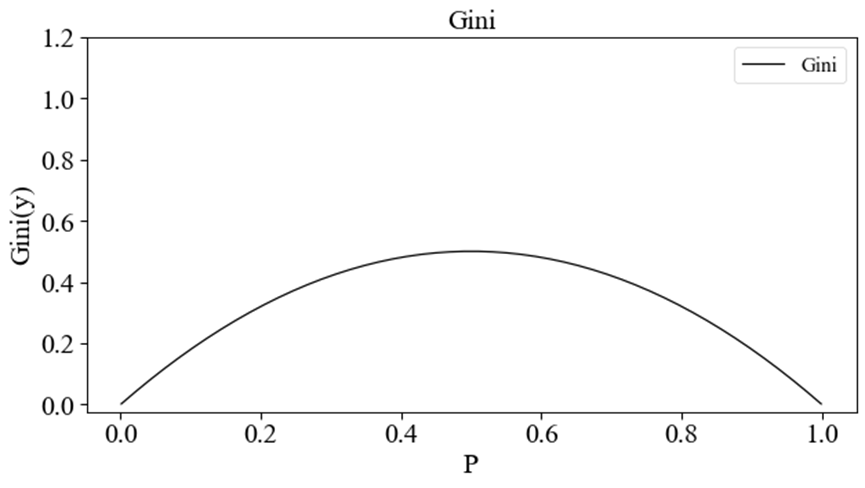
同理,基尼系数也可以作为信息的度量方法。
1.2.3 信息增益
在定义好不确定性的度量标准后,我们便把问题转向了如何来获取“信息量”的大小。为加深直观印象,先假设数据集D=(x1,y1),…,(xn,yn)D={(x_1,y_1 ),…,(x_n,y_n)}D=(x1,y1),…,(xn,yn),其中xi=(xi1,…xin)x_i=(x_i1,…x_in)xi=(xi1,…xin)是描述xix_ixi的nnn维特征。此时以xix_ixi的第m(m<n)m(m<n)m(m<n)个特征ximx_{im}xim为例,那么所谓的信息增益,反映的就是特性ximx_{im}xim所能带来的关于yiy_iyi的“信息量”大小。
可以引入条件熵H(y│A)H(y│A)H(y│A)的概念来定义信息增益。所谓条件熵,就是在xix_ixi第mmm个特征ximx_{im}xim的不同取值限制下的各个部分的不确定性以取值本身的概率加权求和的计算结果。(可以这么理解,假设YYY的某个特征AAA由mmm个取值,即A=a1,…amA={a_1,…a_m }A=a1,…am,依次用这些特征对yyy限制,分别计算被其限制的yyy的信息熵,再把这些信息熵根据限制特征本身的概率加权求和,即得到条件熵)
我们先认可该结论:条件熵H(y│A)H(y│A)H(y│A)越小,就意味着yyy被AAA限制后的总的不确定性越小,从容决策的结果更加有可信度。
条件熵的数学定义如下: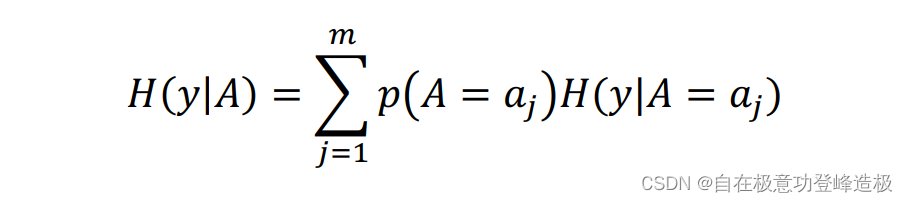
其中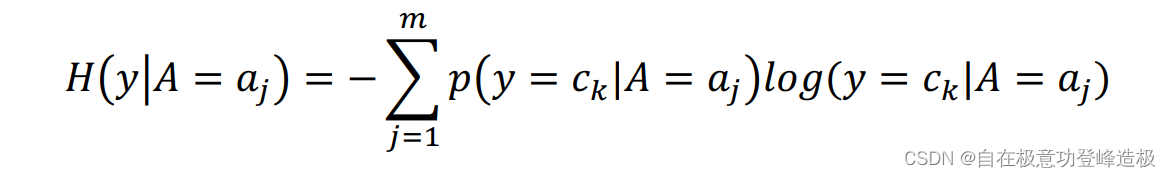
同样用经验条件熵来估计条件熵: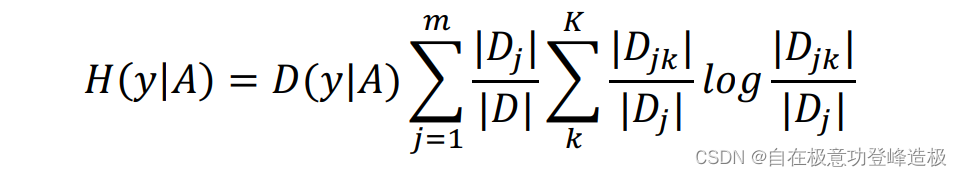
从条件熵出发,我们先定义互信息(𝑀𝑢𝑡𝑢𝑎𝑙 𝐼𝑛𝑓𝑜𝑟𝑚𝑎𝑡𝑖𝑜𝑛) :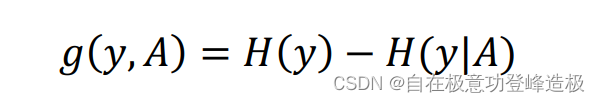
决策树中ID3ID3ID3算法就是利用互信息作为特征选取标准的。但是由于以g(y,A)g(y,A)g(y,A)作为标准的话,会存在偏向于选择取值较多的特征。我们可以知道,若选择的特征较多,自然数据集被划分的也就越多,于是其不确定性自然减少的就越多,这么做显然是不尽合理的。
为解决该问题,可以给mmm一个惩罚,由此可以得到信息增益比(InformationGainRatio)(Information Gain Ratio)(InformationGainRatio)的定义,该定义对应决策树中C4.5C4.5C4.5算法。
其公式如下;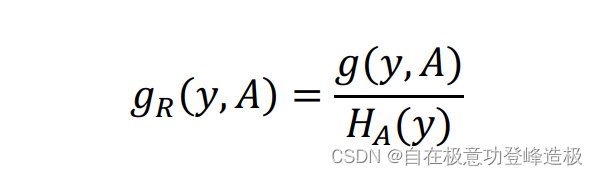
其中HA(y)H_A (y)HA(y)是yyy关于AAA的熵,它的公式是: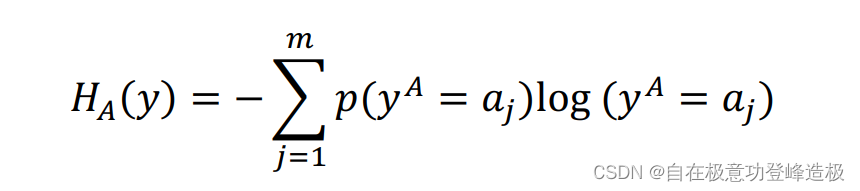
同样用经验熵来进行估计: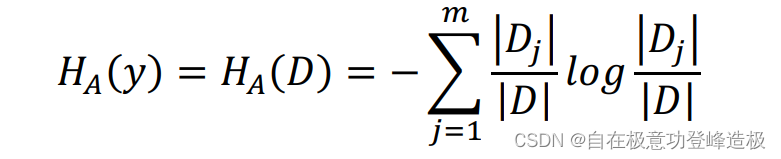
拓展(C5.0C5.0C5.0使用更少的内存,并建立比C4.5C4.5C4.5更小的规则集,同时更准确。)
同理,利用基尼系数来定义信息增益。先定义条件基尼系数: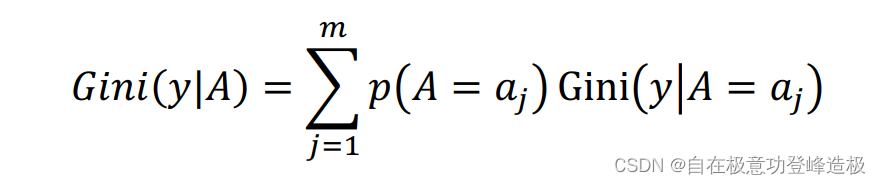
其中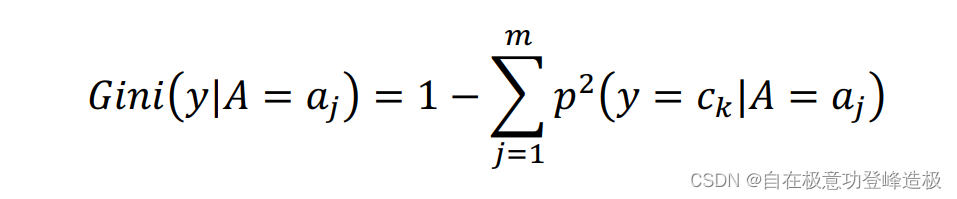
同样用经验条件基尼系数来进行估计: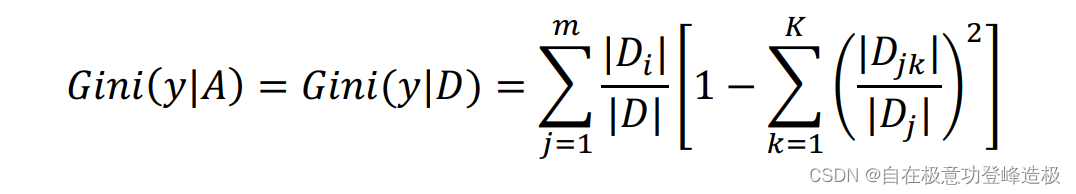
信息增益定义为“基尼增益”: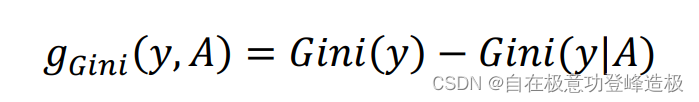
决策树的𝐶𝐴𝑅𝑇算法通常使用该定义。
2、决策树的生成
上节阐述了决策树的算法原理,但我们对于决策树的理解还是过
于抽象,接下来本节将以维基百科上𝑃𝑙𝑎𝑦 𝑔𝑜𝑙𝑓 𝑑𝑎𝑡𝑎𝑠𝑒𝑡数据集详细阐
述决策树的生成过程,以便读者对决策树的生成有一个直观的理解。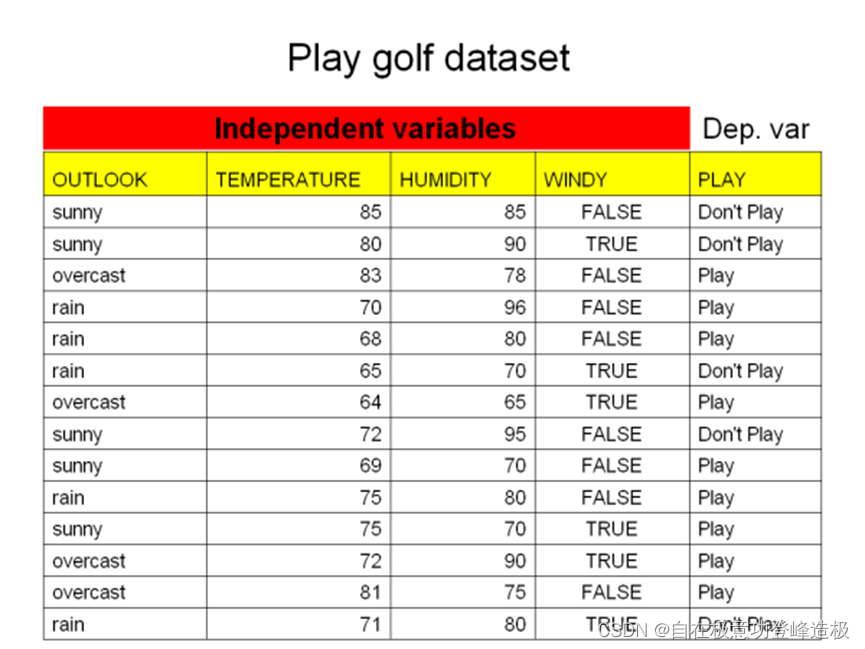
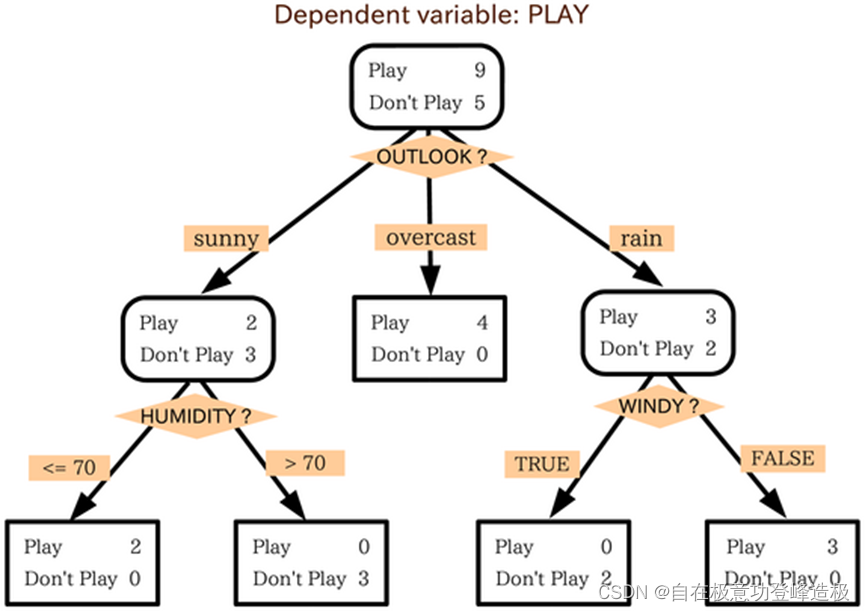
决策树做为一种Tree模型,那它包含了哪些树的结构呢?图2基本蕴含了决策树中所有的关键结构,下面来分开介绍他们。
- 首先是上节提到的“划分标准”这个概念(如信息增益、信息增益比、基尼增益)。图2中被菱形框起来的橙色模块就是作为划分标准的特征,其往下延伸出的橙色矩形方框就是对应特征的各个取值。
- 其次是节点(Node)的概念。在理解图2之前,我们可以把它想象成一颗倒着生长的树,图2中被黑色边框框起来的部分就称为节点。这些Node作为Tree的组成部分,我们称最上方的的Node为“根节点(Root)”,他也是树生长的起点。而用黑色方框(亦即四个角是直角的方框)表示的Node称为树的“叶节点(Leaf)”,从图2不难发现,叶节点是整棵树生长的终点。
- 最后,通常我们还会称一些非叶节点有一些“下属叶节点”。如图2中,所有的叶节点是根节点的下属叶节点,从上往下数第三排左侧的叶节点,是第二排左边圆角方框的节点的下述叶节点。
- 此外,图2中箭头所指的方向代表树的生长方向。我们一般称箭头的起点是终点的“父节点”,终点是起点的“儿子节点”。而左右子节点等与本文联系不大,这里不在赘述。
从图2可以看出,决策树的每个叶节点对应着原样本空间的一个子空间,并且这些子空间两两不相交,全部并起来恰好又是整个样本空间,换言之,决策树的生成可以概括为以下两步:
- 将原始样本空间划分为若干互不相交的子空间。
- 给每一个子空间赋予一个类别标签。
对决策树有了直观认识后,我们来简要梳理下决策树的三大基本算法:
- ID3算法作为最基本的算法,他给出了对离散型数据分离的方法。
- C4.5算法在其基础上进一步发展,给出了混合型数据分类的方法。
- CART算法择更进一步,给出了回归问题的解决方案。
可见决策树算法的功能越来越强大,但其核心思想都是一致的:算法通过不断划分数据集来生成决策树,其每一步的划分都能使当前的信息增益达到最大。
值得一提的是,该核心思想具有机器学习的普适性意义,模型的损失就是数据集的不确定性,模型算法就是最小化这个不确定性的过程。其次,在从参数空间中寻求最优划分特征时,我们每次会选取一个局部最优解(每次选取对数据集进行划分使得信息增益最大化的特征),并把这些局部最优解合成最终解(数据划分序列)。
同样为加深读者对决策树生成过程的理解,笔者以以下流程图说明决策树的生成的过程。
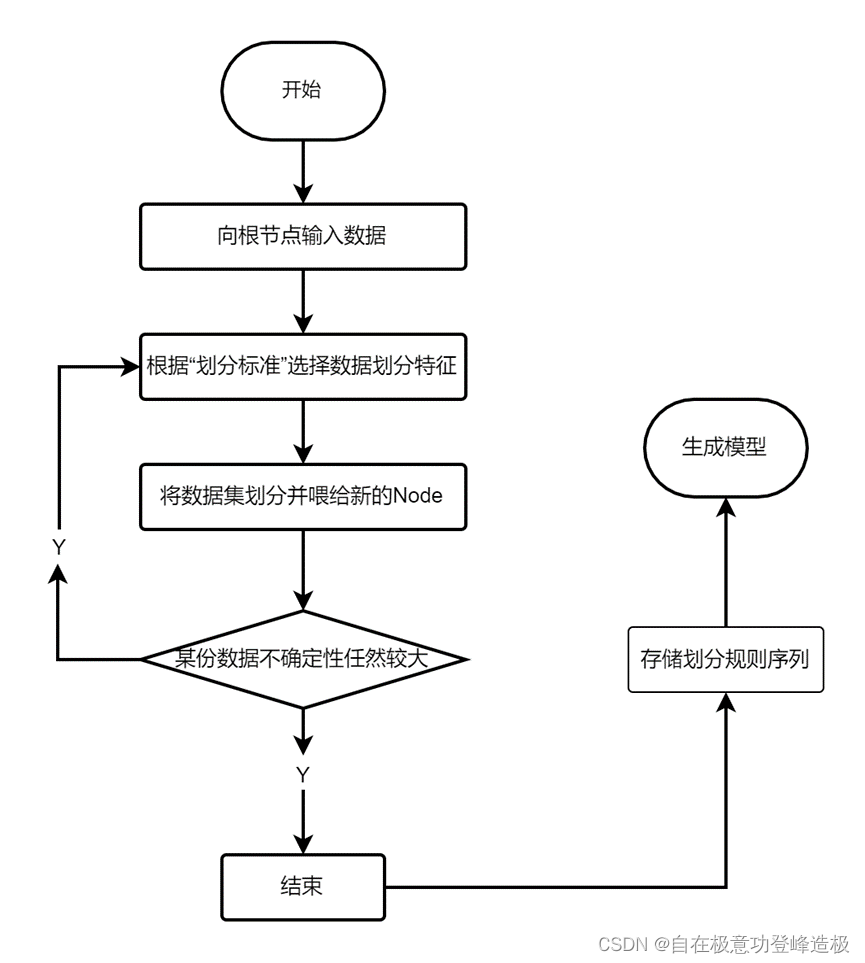
从上述过程可知,决策树的生成过程就是根据某个度量从数据集中训练出一系列的划分规则,使得这些划分规则能够在数据集上有很好的表现。而三种不同的算法在模型的表现上区别仅在于度量信息增益和划分依据的不同上。
3、代码实现

本节笔者将以上述西瓜数据集2.0为例,采用sklearn包进行ID3算法与CART算法的实现。代码及分类效果如下所示。
3.1 ID3算法
from sklearn import tree
import graphviz
import pandas as pd
data = pd.read_excel("西瓜数据集.xlsx")
# 数字编码
data.色泽 = data.色泽.replace(['青绿','乌黑','浅白'],[0,1,2])
data.根蒂 = data.根蒂.replace(['蜷缩','稍蜷','硬挺'],[0,1,2])
data.敲声 = data.敲声.replace(['浊响','沉闷','清脆'],[0,1,2])
data.纹理 = data.纹理.replace(['清晰','稍糊','模糊'],[0,1,2])
data.脐部 = data.脐部.replace(['凹陷','稍凹','平坦'],[0,1,2])
data.触感 = data.触感.replace(['硬滑','软粘'],[0,1])
# criterion选择entropy,这里表示选择ID3算法
model = tree.DecisionTreeClassifier(criterion='entropy', splitter='best')
result = model.fit(data.iloc[:,1:-1], data.iloc[:,-1])
dot_data = tree.export_graphviz(result, out_file=None,
feature_names=data.iloc[:,1:-1].columns.tolist(),
class_names= data.iloc[:,-1].unique(),
filled=True,
rounded=True,
special_characters=True)
graph_1 = graphviz.Source(dot_data)
graph_1
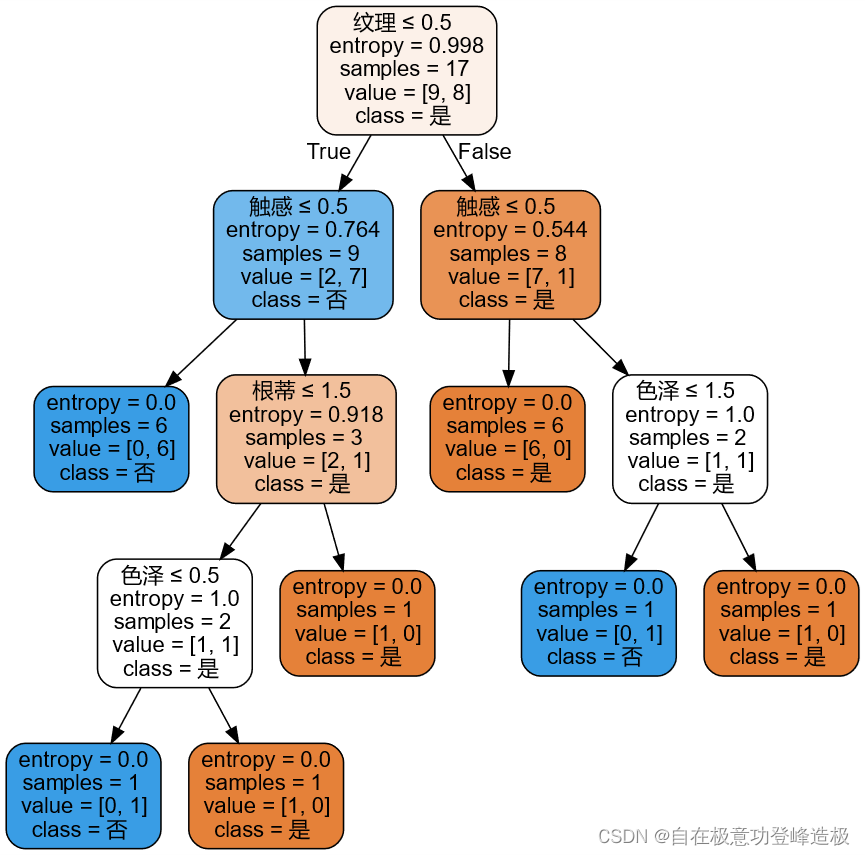
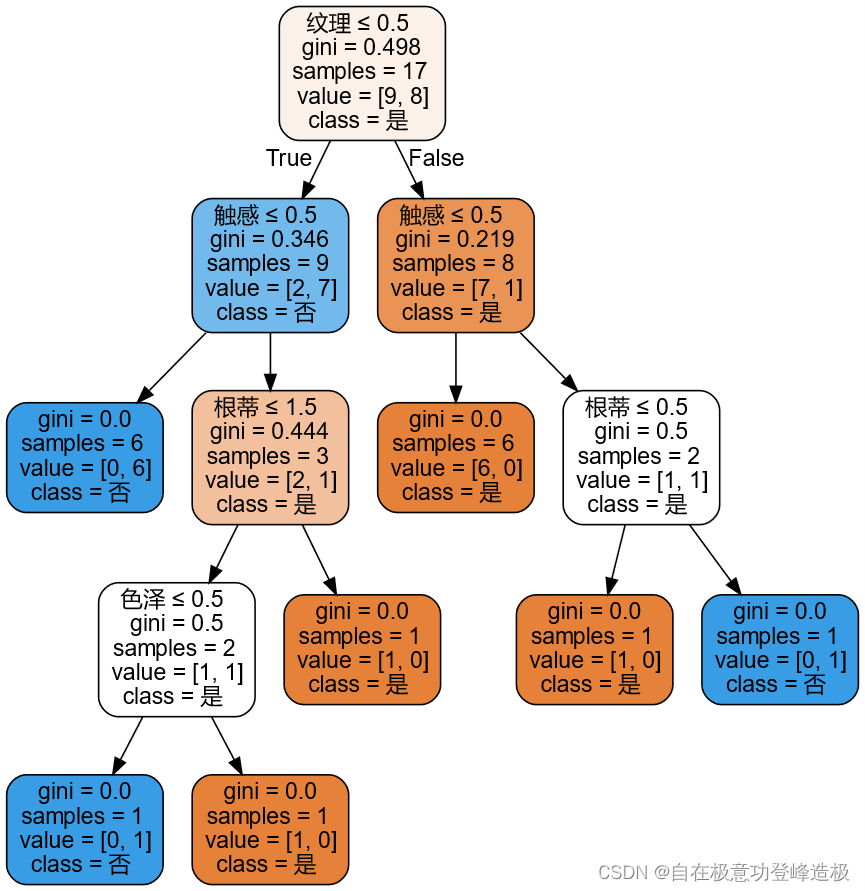
3.2 CART算法
data = pd.read_excel("西瓜数据集.xlsx")
# 数字编码
data.色泽 = data.色泽.replace(['青绿','乌黑','浅白'],[0,1,2])
data.根蒂 = data.根蒂.replace(['蜷缩','稍蜷','硬挺'],[0,1,2])
data.敲声 = data.敲声.replace(['浊响','沉闷','清脆'],[0,1,2])
data.纹理 = data.纹理.replace(['清晰','稍糊','模糊'],[0,1,2])
data.脐部 = data.脐部.replace(['凹陷','稍凹','平坦'],[0,1,2])
data.触感 = data.触感.replace(['硬滑','软粘'],[0,1])
# criterion选择entropy,这里表示选择C4.5算法
model = tree.DecisionTreeClassifier(criterion='gini', splitter='best')
result = model.fit(data.iloc[:,1:-1], data.iloc[:,-1])
dot_data = tree.export_graphviz(result, out_file=None,
feature_names=data.iloc[:,1:-1].columns.tolist(),
class_names= data.iloc[:,-1].unique(),
filled=True,
rounded=True,
special_characters=True)
graph_1 = graphviz.Source(dot_data)
更多内容请下载该文档的【资源绑定】查看。

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容







所有评论(0)