前言

本文参考$StevenM.LaValle$的《Planning Algorithms》，针对后驱的simple car来进行分析robot运动学。

模型简介

模型如下，车的坐标系原点在后轮中心位置，此模型为两轮驱动，后两个为驱动轮，前两个为从动轮，前两个掌握方向，后两个输出速度。L为前后轮的距离，如果 $\varphi$定了，那么车将进行圆周运动，运动半径就是$\rho$。

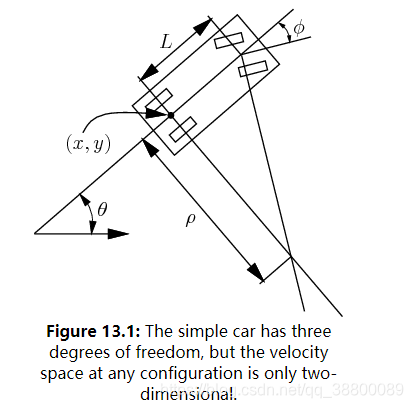
运动学方程表述如下：s是车辆的速度（具有符号），就是沿着车的坐标系x轴的速度；$\varphi$是车轮转向角steering angle，图中的车轮转向是正值。x，y，$\theta$,显而易见。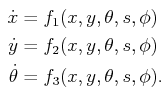

运动学方程推导

当在一个非常小的时间间隔$\Delta t$内，汽车的方向大概就可以认为是后轮的朝向。当$\Delta t$趋近于0，则$dy/dx=\dot{y}/\dot{x}$，而且在世界坐标系中 $dy/dx=\tan \theta$ ，结合 $\tan \theta =\sin \theta /\cos \theta$可以得到Pfaffian constraint：
$$-\dot{x}\sin \theta +\dot{y}\cos \theta =0$$
由这个式子可以知道， $\dot{x}=\cos \theta$ 和$\dot{y}=\sin \theta$满足上面的约束或者说是上面方程的解，而且这个解的倍数也是这个方程的解。在这个模型中这个倍数就是s（车的后轮速度），所以运动学的前两项就求出来了
$$\begin{gathered} \dot{x}=s\cos \theta \\ \dot{y}=s\sin \theta \end{gathered}$$

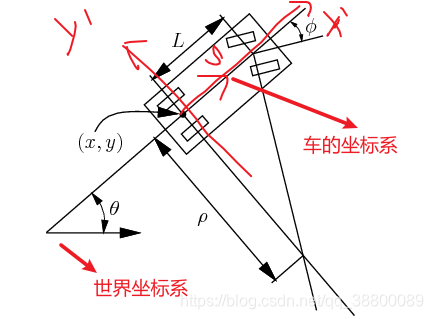
最后推导$\dot{\theta }$的表达式，由这个模型知道，当$\varphi$固定了，车辆行驶的弧长就是$w$，那么有
$dw=\rho d\theta$，再由$\rho =L/\tan \varphi$，我们能得到：
$$d\theta =\frac{\tan \varphi }{L}dw两边分别除以dt得\dot{\theta }=\frac{s}{L}\tan \varphi$$

运动学方程为：
$$\begin{gathered} \dot{x}=s\cos \theta \\ \dot{y}=s\sin \theta \\ \dot{\theta }=\frac{s}{L}\tan \varphi \end{gathered}$$

在上面这个模型中，我们能控制的变量是速度s和车转向$\varphi$，其中s根据实际车来定，这个牵扯到动力学，而$\varphi$值在$(-{\varphi }_{max},{\varphi }_{max})$之间，且${\varphi }_{max}<\pi /2$，最小转弯半径为${\rho }_{min}=L/\tan {\varphi }_{max}$。