【模拟电子技术Analog Electronics Technology 20】—— 反馈放大电路分析2:各种类型反馈电路的计算分析
文章目录1.反馈放大电路的各项指标1.1 反馈放大电路闭环增益的一般表达式:2. 深度负反馈放大电路放大倍数的详细分析1.反馈放大电路的各项指标上图中,XiX_iXi表示总输入,Xi′X_i'Xi′表示净输入,XfX_fXf表示反馈量;A模块表示放大电路,F模块表示反馈电路。大家注意一下上面方框图的箭头:它表示反馈只能从输出流向输入,整个电路的流动必须按照这个箭头走,不能变!(这也是后...
1.反馈放大电路的各项指标
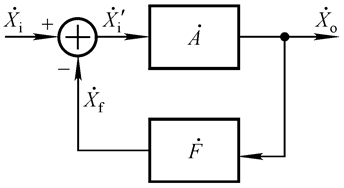
上图中, X i X_i Xi表示总输入, X i ′ X_i' Xi′表示净输入, X f X_f Xf表示反馈量;A模块表示放大电路,F模块表示反馈电路。大家注意一下上面方框图的箭头:它表示反馈只能从输出流向输入,整个电路的流动必须按照这个箭头走,不能变!(这也是后面我们计算时的依据)
假设是负反馈,那么我们有: X i ′ = X i − X f X_i' = X_i - X_f Xi′=Xi−Xf
下面,我们定义几个指标: 开 环 增 益 A = X 0 X i ′ 开环增益A = \frac{X_0}{X_i'} 开环增益A=Xi′X0
反 馈 系 数 F = X f X 0 反馈系数F = \frac{X_f}{X_0} 反馈系数F=X0Xf
闭 环 增 益 A f = X 0 X i 闭环增益A_f = \frac{X_0}{X_i} 闭环增益Af=XiX0
环 路 增 益 A F = A ∗ F = X f X i ′ 环路增益AF = A * F = \frac{X_f}{X_i'} 环路增益AF=A∗F=Xi′Xf
下面我们依次看看不同反馈形式下这些量都是什么:
| 反馈方式 | X i X_i Xi | X f X_f Xf | X i ′ X_i' Xi′ | X 0 X_0 X0 | A | F | A f A_f Af |
|---|---|---|---|---|---|---|---|
| 电压串联 | U i U_i Ui | U f U_f Uf | U i ′ U_i' Ui′ | U 0 U_0 U0 | U 0 U i ′ \frac{U_0}{U_i'} Ui′U0 | U f U 0 \frac{U_f}{U_0} U0Uf | U 0 U i \frac{U_0}{U_i} UiU0 |
| 电压并联 | I i I_i Ii | I f I_f If | I i ′ I_i' Ii′ | U 0 U_0 U0 | U 0 I i ′ \frac{U_0}{I_i'} Ii′U0 | I f U 0 \frac{I_f}{U_0} U0If | U 0 I i \frac{U_0}{I_i} IiU0 |
| 电流串联 | U i U_i Ui | U f U_f Uf | U i ′ U_i' Ui′ | I 0 I_0 I0 | I 0 U i ′ \frac{I_0}{U_i'} Ui′I0 | U f I 0 \frac{U_f}{I_0} I0Uf | I 0 U i \frac{I_0}{U_i} UiI0 |
| 电流并联 | I i I_i Ii | I f I_f If | I i ′ I_i' Ii′ | I 0 I_0 I0 | I 0 I i ′ \frac{I_0}{I_i'} Ii′I0 | I f I 0 \frac{I_f}{I_0} I0If | I 0 I i \frac{I_0}{I_i} IiI0 |
1.1 反馈放大电路闭环增益的一般表达式:
我们知道: A f = X 0 X i = X 0 X i ′ + X f = A X i ′ X i ′ + A F X i ′ = A 1 + A F A_f = \frac{X_0}{X_i} = \frac{X_0}{X_i' + X_f} = \frac{AX_i'}{X_i' + AFX_i'} = \frac{A}{1 + AF} Af=XiX0=Xi′+XfX0=Xi′+AFXi′AXi′=1+AFA
当电路引入深度负反馈时,我们有: X f ≈ X i X_f ≈ X_i Xf≈Xi(即净输入基本为0)
那么, A f F ≈ 1 A_fF ≈1 AfF≈1
即 A f = 1 F A_f = \frac{1}{F} Af=F1
【在一般的用集成运放组成的电路中, A f = 1 F A_f = \frac{1}{F} Af=F1】
这一小段,我们暂时浅尝辄止,等下几篇博文再回过头来仔细分析它,因为我们现在了解到这里就够我们去计算了
2. 深度负反馈放大电路放大倍数的详细分析
一,电压串联负反馈
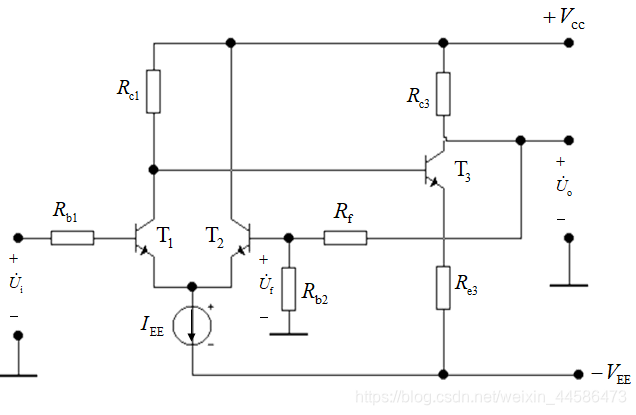
首先,我们知道,反馈是由 R f , R b 2 R_f, R_{b2} Rf,Rb2组成的通路,由于是电压串联负反馈,那么放大倍数 A f A_f Af即为 U 0 U i = 1 F \frac{U_0}{U_i} = \frac{1}{F} UiU0=F1
还记得我们上面说得吗:反馈通路只能由输出流回输入,不能从输入流向输出,因此,对于串联反馈,我们就把输入回路于反馈之间的路给切了,如下图所示:
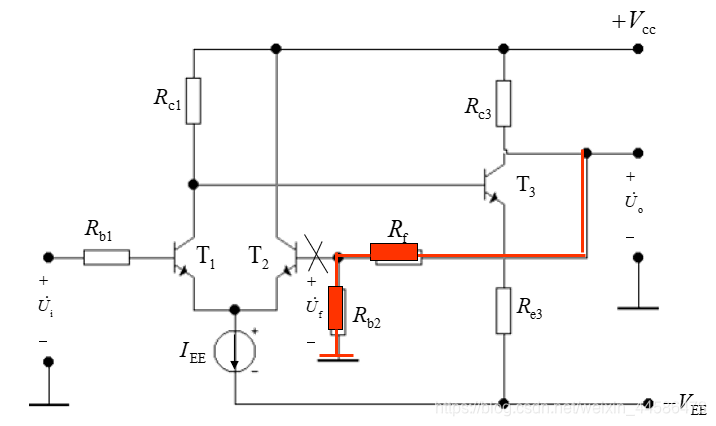
这样一来, R f R_f Rf与 R b 2 R_{b2} Rb2就是串联关系了,那么 U f = R b 2 R b 2 + R f U 0 U_f = \frac{R_{b2}}{R_{b2} + R_f}U_0 Uf=Rb2+RfRb2U0
那么, F = U f U 0 = R b 2 R b 2 + R f F = \frac{U_f}{U_0} = \frac{R_{b2}}{R_{b2}+R_f} F=U0Uf=Rb2+RfRb2
因此, A f = 1 F = R b 2 + R f R b 2 A_f = \frac{1}{F} = \frac{R_{b2} + R_f}{R_{b2}} Af=F1=Rb2Rb2+Rf
二,电流串联负反馈
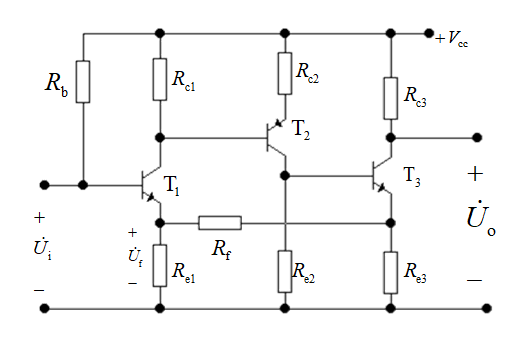
我们能看到,反馈的支路是 R e 3 , R f , R e 1 R_{e3}, R_f, R_{e1} Re3,Rf,Re1组成的通路,同样的,由于是串联反馈,所以我们要把输入和反馈通路相连的部分断开,如下图所示
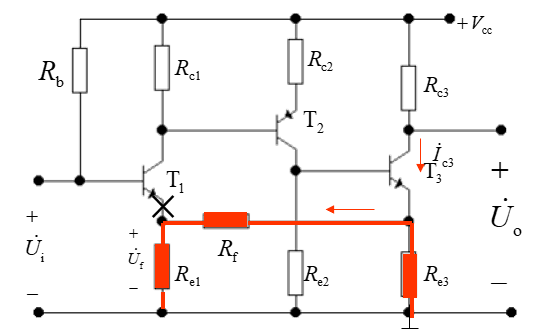
那么,这样就是 R e 1 R_{e1} Re1与 R f R_f Rf的串联之后再和 R e 3 R_{e3} Re3并联了,要求 U f U_f Uf就是求 R e 1 , R f R_{e1}, R_f Re1,Rf支路的分流:
I ′ = R e 3 R e 3 + R f + R e 1 I c 3 I' = \frac{R_{e3}}{R_{e3} + R_f + R_{e1}}I_{c3} I′=Re3+Rf+Re1Re3Ic3(这里近似 I c 3 = I e 3 I_{c3} = I_{e3} Ic3=Ie3)
那么, U f = R e 1 I ′ = R e 3 R e 1 R e 3 + R f + R e 1 I c 3 U_f = R_{e1}I' = \frac{R_{e3}R_{e1} }{R_{e3} + R_f + R_{e1}}I_{c3} Uf=Re1I′=Re3+Rf+Re1Re3Re1Ic3
F = U f I c 3 = R e 3 R e 1 R e 3 + R f + R e 1 F = \frac{U_f}{I_{c3}} = \frac{R_{e3}R_{e1} }{R_{e3} + R_f + R_{e1}} F=Ic3Uf=Re3+Rf+Re1Re3Re1
那么, A f = I c 3 U i = 1 F = R e 3 + R f + R e 1 R e 3 R e 1 A_f = \frac{I_{c3}}{U_i} = \frac{1}{F} = \frac{R_{e3} + R_f + R_{e1}}{R_{e3}R_{e1} } Af=UiIc3=F1=Re3Re1Re3+Rf+Re1
但是,我们想求 U i U_i Ui与 U 0 U_0 U0的关系,即:
A u f = U 0 U i A_{uf} = \frac{U_0}{U_i} Auf=UiU0
U 0 U_0 U0怎么求呢?在交流通路中,那个 R c 3 R_{c3} Rc3是要被翻下来的,所以 U 0 = − I c 3 R c 3 U_0 = -I_{c3}R_{c3} U0=−Ic3Rc3
所以我们可以得到: A u f = − R c 3 A f = − R e 3 + R f + R e 1 R e 3 R e 1 R c 3 A_{uf} = -R_{c3}A_f = -\frac{R_{e3} + R_f + R_{e1}}{R_{e3}R_{e1} }R_{c3} Auf=−Rc3Af=−Re3Re1Re3+Rf+Re1Rc3
三,电压并联负反馈
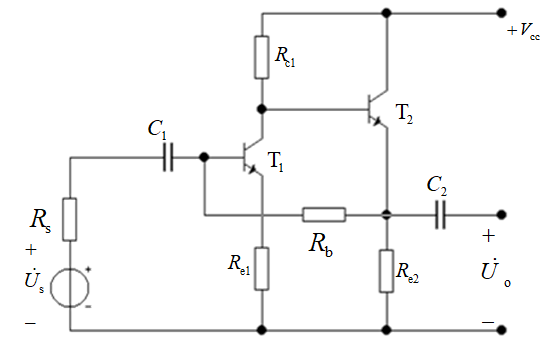
我们可以知道,反馈通路是 C 2 , R b C_2, R_b C2,Rb组成的那条支路,对于并联反馈,我们把反馈和输入相连的地方接地处理,如下图所示:
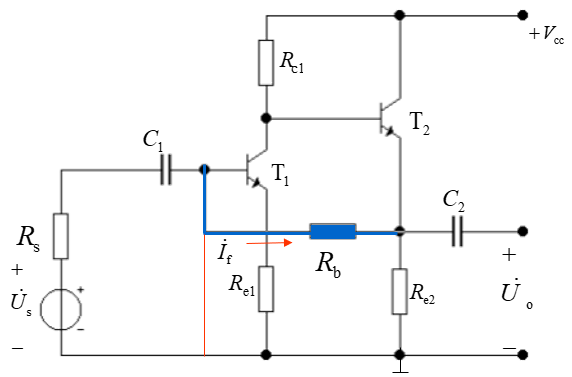
蓝色线代表原来的反馈通路,红色线代表接地处理之后的连接方式
F = I f U 0 = − U 0 R b U 0 = − 1 R b F = \frac{I_f}{U_0} = \frac{-\frac{U_0}{R_{b}}}{U_0} = -\frac{1}{R_{b}} F=U0If=U0−RbU0=−Rb1
因此, A f = U 0 I f = 1 F = − R b A_f = \frac{U_0}{I_f} = \frac{1}{F} = -R_b Af=IfU0=F1=−Rb
同样地,我们会需要计算输入输出电压之间的关系: A u f = U 0 U i = U 0 I i R i f A_{uf} = \frac{U_0}{U_i} =\frac{U_0}{I_iR_{if}} Auf=UiU0=IiRifU0
其中, R i f R_{if} Rif是反馈放大电路的输入电阻
由于在深度负反馈下,有 I i ≈ I f I_i ≈ I_f Ii≈If
因此, A u f ≈ U 0 I f R i f A_{uf} ≈ \frac{U_0}{I_fR_{if}} Auf≈IfRifU0
可是,在深度负反馈下, R i f R_{if} Rif趋近于0,因此电压放大倍数相当大的
所以,我们便考虑计算输出电压与电源电压的关系,即: A u s f = U 0 U s = U 0 I i ( R i f + R s ) ≈ U 0 I f ( R i f + R s ) A_{usf} =\frac{U_0}{U_s} = \frac{U_0}{I_i(R_{if} + R_s)} ≈ \frac{U_0}{I_f(R_{if} + R_s)} Ausf=UsU0=Ii(Rif+Rs)U0≈If(Rif+Rs)U0
由于 R i f − > 0 R_{if} -> 0 Rif−>0,因此: A u s f = U 0 I f R s = A f R s = − R b R s A_{usf} = \frac{U_0}{I_fR_s} = \frac{A_f}{R_s} = \frac{-R_b}{R_s} Ausf=IfRsU0=RsAf=Rs−Rb
四,电流并联
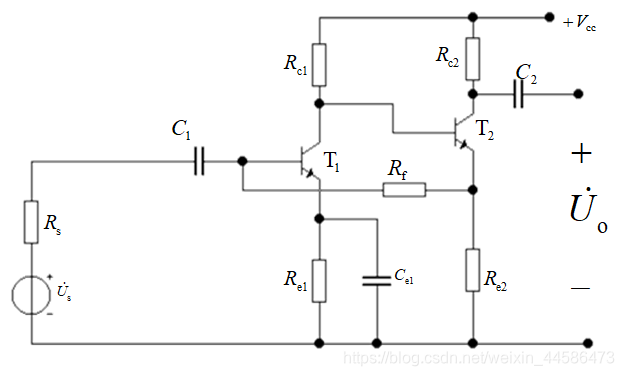
同理,我们时刻记得输出不能从反馈支路流向输出,反馈支路是专门给输出流回输出的,因此,在并联负反馈情况下,我们要将反馈支路和输入相接的地方接地,如下图所示: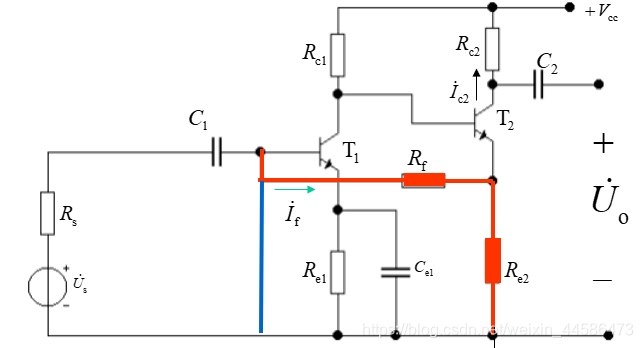
由于是电流并联负反馈,因此,输入 X i X_i Xi是电流 I i I_i Ii, X f X_f Xf是电流 I f I_f If,输出也是电流 I o I_o Io
那么, F = X f X o = I f I o = R e 2 R f + R e 2 F = \frac{X_f}{X_o} = \frac{I_f}{I_o} = \frac{R_{e2}}{R_f + R_{e2}} F=XoXf=IoIf=Rf+Re2Re2
但是,有些时候,我们常常想找出输出电压和输入电压之间的关系,那么,我们来试着写写:
A u f = U o U i = I c 2 R c 2 I i R i f A_{uf} = \frac{U_o}{U_i} = \frac{I_{c2}R_{c2}}{I_iR_{if}} Auf=UiUo=IiRifIc2Rc2
可是,在深度负反馈下, R i f R_{if} Rif趋近于0,因此电压放大倍数相当大的,因此我们只能看看输出电压和电压源电压之间的关系,即:
A u s f = U o U s = I c 2 R c 2 I i ( R i f + R s ) ≈ I c 2 R c 2 I i R s A_{usf} = \frac{U_o}{U_s} = \frac{I_{c2}R_{c2}}{I_i(R_{if} + R_s)}≈ \frac{I_{c2}R_{c2}}{I_iR_s} Ausf=UsUo=Ii(Rif+Rs)Ic2Rc2≈IiRsIc2Rc2
即: A u s f ≈ I 0 R c 2 I f R s = R f + R e 2 R e 2 R c 2 R s A_{usf} ≈ \frac{I_{0}R_{c2}}{I_fR_s} = \frac{R_f + R_{e2}}{R_{e2}}\frac{R_{c2}}{R_s} Ausf≈IfRsI0Rc2=Re2Rf+Re2RsRc2

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容






所有评论(0)