一、算法复杂度

算法作为一个程序的核心，其复杂度能够影响着它的效率，那么我们该如何衡量呢？其实可以将复杂度分为两个维度——空间复杂度以及时间复杂度。

空间复杂度简单来说就是对一个算法在运行过程中临时额外占用存储空间大小的量度，而时间复杂度则是一个算法运行速度快慢的量度，如今计算机硬件飞速发展，空间复杂度在大部分情况下不用特别地去考虑，本篇文章主要是为大家讲解时间复杂度以及其简单计算。

二、时间复杂度

2.1 时间复杂度的概念

时间复杂度并不是算法具体的执行时间，而是用来描述算法执行时间随着输入数据规模增大而增长的速度,大家可以理解为算法中基本操作的执行次数。

比如，对一个数组进行排序，当数组元素个数从 10 增加到 100 时，算法运行时间会如何变化，时间复杂度就是用来刻画这种变化规律的。

当然，作为衡量代码速度的依据，当代码较多时我们不可能一条条去数，那么我们该如何判断呢？

2.2 大O渐近表示法

2.2.1 概念

算法一般是以估量值来判断其时间复杂度，人们常用大O渐近表示法来粗略估计一个算法的时间复杂度。

通常使用大 O 符号（Big O notation）来表示时间复杂度。大 O 符号描述的是算法在最坏情况下的时间复杂度，它给出了算法执行时间的上界。其数学定义为：如果存在正常数 c 和 ，使得当 n ≥ 时，T(n) ≤ c⋅f(n)，则称 T(n)=O(f(n))，其中 T(n) 是算法的实际执行时间，f(n) 是一个函数，代表算法时间复杂度的增长趋势，n 是输入数据的规模。

2.2.2 计算步骤

1.找出算法中的基本语句

2.计算其运行次数数量级

3.保留最高数量级，忽略系数

4.大O符号表示

举个例子：

void func1(int arr[], int n) {
    int i, j, min_idx;
    for (i = 0; i < n - 1; i++) {             //第一层
        min_idx = i;
        for (j = i + 1; j < n; j++) {         //第二层
            if (arr[j] < arr[min_idx]) {
                min_idx = j;
            }
        }
        int temp = arr[min_idx];
        arr[min_idx] = arr[i];
        arr[i] = temp;
    }
}

这是一个选择排序的函数，我们根据上面的计算步骤来算一下他的时间复杂度

1.找出算法中的基本语句:

       if (arr[j] < arr[min_idx]) 

2.计算其运行次数数量级: 

      外层循环：变量 i 从 0 递增到 n - 2 ，总共执行了 n - 1 次循环。

      内层循环：对于外层循环的每一次迭代，内层循环的执行次数是不同的。

                        当 i = 0 时，内层循环中 j 从 1 到 n - 1，执行 n - 1 次。

                        当 i = 1 时，内层循环中 j 从 2 到 n - 1，执行 n - 2 次。

                        以此类推，当 i = n - 2 时，内层循环中 j 从 n - 1到 n - 1，执行 1 次。

      所以，基本语句 if (arr[j] < arr[min_idx]) 的执行总次数是一个等差数列的和，根据等差数列求和公式，这里的总和 S 为：

 

3.保留最高数量级，忽略系数：

      幂次最高项为  ，忽略系数 

4.大O符号表示

      用大 O 符号表示该算法的时间复杂度为 

5.综上所述，该函数的时间复杂度是 

 根据以上步骤，大多数的算法时间复杂度计算就都能迎刃而解了，下面会给出一些典型的函数时间复杂度计算。

三、常见时间复杂度计算

3.1 常数时间复杂度

常数时间复杂度意味着算法的执行时间不随输入数据规模的增大而变化，无论输入数据有多少，算法总是在固定的步骤内完成操作，记为 O(1) 。

例如交换两个整数值的函数：

void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

3.2 线性时间复杂度

线性时间复杂度表示算法的执行时间与输入规模成正比，即输入规模增加一倍，算法的执行时间也大致增加一倍，记为 O(n) 。

 例如计算数组中所有元素和的函数：

int sumArray(int arr[], int n) {
    int sum = 0;
    for (int i = 0; i < n; i++) {
        sum += arr[i];
    }
    return sum;
}

复杂度分析：

这其中包含了一层 for 循环，即数组中每个数都遍历了一次，因此执行时间随数组长度 n 的增加而线性增长，时间复杂度为 O(n) 。

3.3 平方时间复杂度

平方时间复杂度的算法通常包含两层嵌套循环，执行时间随着输入规模的平方增长，记为 。

例如冒泡排序函数：

void bubbleSort(int arr[], int n) {
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

复杂度分析：

冒泡排序使用两层嵌套循环，外层循环执行  n - 1 次，内层循环的执行次数随着外层循环的进行而逐渐减少，但总的执行次数大致为 ，因此时间复杂度为 。

注： 对于这类嵌套函数，很多同学习惯看到循环就算作 n 次，大家计算的时候要注意循环次数是否是 n + C(常数）次。

3.4 开方时间复杂度

 开方时间复杂度通常用于排序过程的优化等，记为 。

例如判断一个数是否为完全平方数：

bool isPerfectSquare(int n) {
    for (int i = 1; i * i <= n; i++) {
        if (i * i == n) {
            return true;
        }
    }
    return false;
}

复杂度分析：

代码中使用了一个 for 循环，循环变量 i 从 1 开始，直到  为止。在最坏情况下，循环会执行  次，因此该算法的时间复杂度为  。

3.5 对数时间复杂度

对数时间复杂度的算法通常通过不断将问题规模缩小一半来解决问题，记为 O(logn) 。

 例如二分查找算法：

int binarySearch(int arr[], int left, int right, int target) {
    while (left <= right) {
        int mid = left + (right - left) / 2;

        if (arr[mid] == target) {
            return mid;
        } else if (arr[mid] < target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    return -1;
}

复杂度分析：

每次迭代，二分查找都会将搜索范围缩小一半。假设数组长度为 n，最多需要 次迭代就可以找到目标元素（或确定目标元素不存在），因此时间复杂度为O(logn) 。

注：描述对数函数时间复杂度时一般可省略底数，根据对数的换底公式，对于任意两个不同底数a和b，和之间存在关系，其中是一个常数。在时间复杂度的分析中，常数倍的差异不影响算法的渐近性能，所以可以忽略底数，下面的线性对数时间复杂度亦是如此。

 3.6 线性对数时间复杂度

线性对数时间复杂度常见于高效的排序算法，如归并排序和快速排序，记为 O(nlogn) 。

例如归并排序：

// 合并两个已排序的子数组
void merge(int arr[], int left, int mid, int right) {
    int n1 = mid - left + 1;
    int n2 = right - mid;

    int L[n1], R[n2];

    for (int i = 0; i < n1; i++) {
        L[i] = arr[left + i];
    }
    for (int j = 0; j < n2; j++) {
        R[j] = arr[mid + 1 + j];
    }

    int i = 0, j = 0, k = left;

    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }

    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}

// 归并排序函数
void mergeSort(int arr[], int left, int right) {
    if (left < right) {
        int mid = left + (right - left) / 2;

        mergeSort(arr, left, mid);
        mergeSort(arr, mid + 1, right);

        merge(arr, left, mid, right);
    }
}

 复杂度分析：

归并排序将数组不断二分，递归深度为，每次合并操作的时间复杂度为 ，因此总的时间复杂度为  。

 3.7 指数时间复杂度

指数时间复杂度的算法执行时间随着输入规模的增加呈指数级增长，通常用于解决一些组合问题，记为  。

例如斐波那契数列的递归实现：

int fibonacci(int n) {
    if (n <= 1) {
        return n;
    }
    return fibonacci(n - 1) + fibonacci(n - 2);
}

复杂度分析：

在计算斐波那契数列的第 n 项时，递归调用会产生大量的重复计算，每一层递归都会将问题规模拆分成两个子问题，导致计算量呈指数级增长，时间复杂度为 。

四、时间复杂度效率比较

 

 

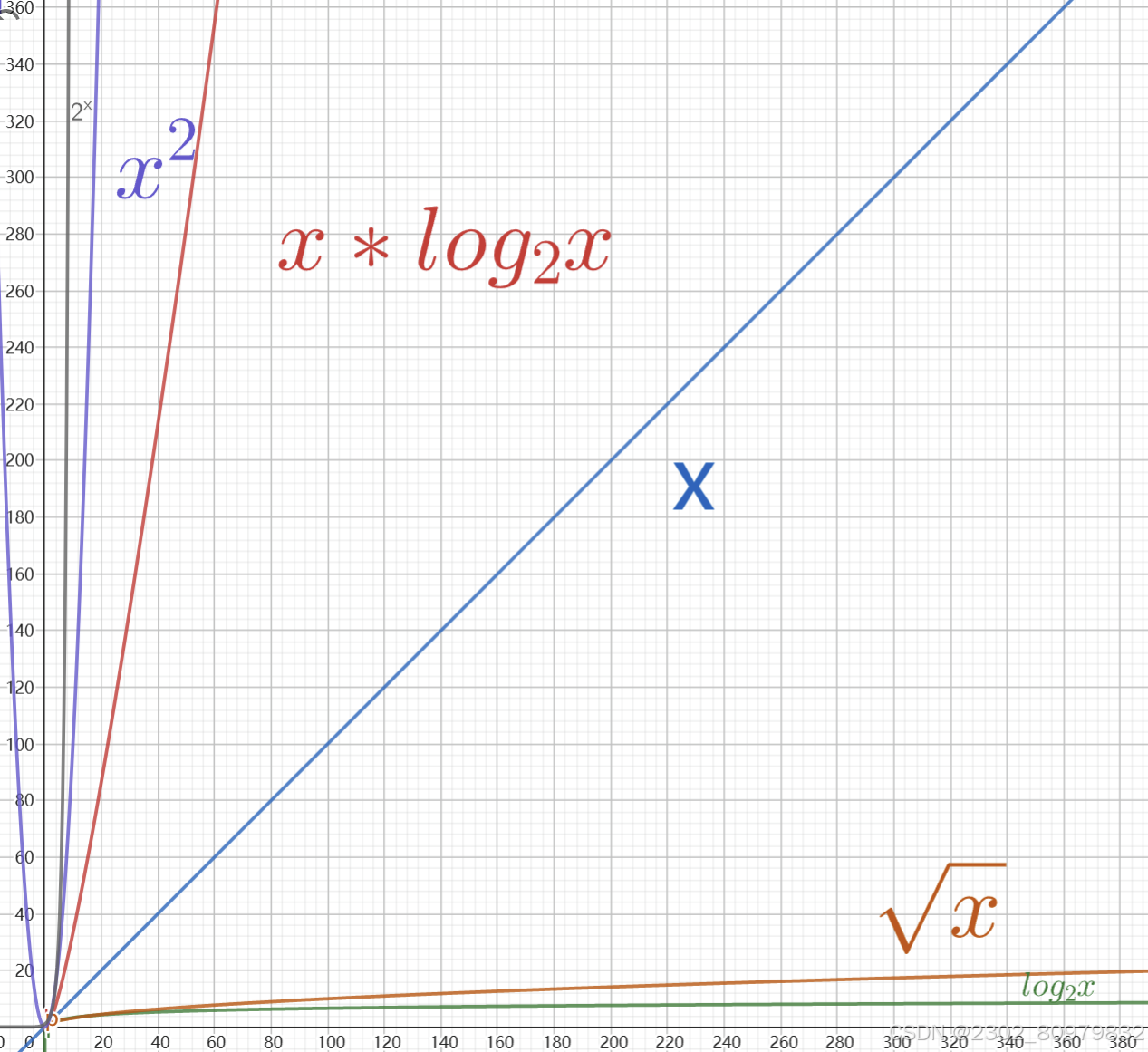
五、 其他方法计算时间复杂度

在计算时间复杂度时可能还有些同学不能立即理解比如对数类以及多次方类的时间复杂度，那么在一些简单问题中，也可以画表来帮助理解时间复杂度的计算，下面举几个例子：

例一： 

for(int i=1; i<=n; i=i*2)
{
    x++;
    s=0;
}

次数	1	2	3	4	t
i	1	2	4	8	?
i(2^n)	0	1	2	3	t-1

由此可得 

解得 

即时间复杂度为 

例二： 

//计算该程序片段时间复杂度
X = 2;
while (x < n/2)
      x = 2 * x;

次数	1	2	3	4	t
x(2^n)	2	3	4	5	t+1

由此可得

解得

即时间复杂度为 

例三：

int func (int n){
    int i = 0, sum = 0;
    while(sum < n) sum += ++i;
    return i;
}

次数	1	2	3	4	t
i	1	2	3	4	t
sum	1	3	6	10	t(t+1)/2

 

由此可得 

即时间复杂度为 

希望这篇文章能够给你带来帮助，如有错漏之处或改进建议，欢迎随时指出，谢谢！