引射器结构

引射器的结构如下，可以通过高速的工作气$v_1$将被引射的气体$v^{\prime }$抽吸带动，实现泵送

被引射气体流速的计算

扩张段的计算

列写不可压流体的质量守恒方程，有
$$v_2=\frac{A_3}{A_2}{v}_3$$
列写不可压流体的伯努利方程，有
$$p_2=p_3+\frac{\rho v_3^2}{2}-\frac{\rho v_2^2}{2}$$

直筒段的计算

以直筒段气体为控制体积，考虑其动量守恒方程，有
$$\rho v_2^2{A}_2-\left(\rho v_1^2{A}_1+\rho v^{\prime 2}\left(A_2-A_1\right)\right)=p_1{A}_1+p_1\left(A_2-A_1\right)-p_2{A}_2$$需要注意的是由于流速较低,式中忽略了壁面对气体的摩擦阻力，工作气喷嘴出口处的压力是均匀的，为$p_1$。
$$p_1=p_0-\rho \frac{v_1^2}{2}$$需要注意的是，$p_0$是工作气的滞止压力。再考虑质量守恒方程，有
$$v_1{A}_1+v^{\prime }\left(A_2-A_1\right)=v_2{A}_2$$

联立求解

引入无量纲的面积比
$${\epsilon }_1=\frac{A_1}{A_2},{\epsilon }_3=\frac{A_3}{A_2}$$
引入压力差
$$\Delta p=p_0-p_3$$联立扩张段质量守恒方程、扩张段伯努利方程、直筒段动量守恒方程和直筒段质量守恒方程，可以求解4个未知量
$$v^{\prime }=\frac{{{\epsilon }_3}^2\sqrt{\frac{2\Delta p\left(({\epsilon }_1+1){{\epsilon }_3}^2+{\epsilon }_1-1\right)+\rho v_1^2\left(({\epsilon }_1-1){{\epsilon }_3}^2-3{\epsilon }_1+1\right)}{({\epsilon }_1-1){{\epsilon }_3}^2\rho }}+{\epsilon }_1\left({{\epsilon }_3}^2+1\right)v_{{}_1}}{({\epsilon }_1+1){{\epsilon }_3}^2+{\epsilon }_1-1}$$$$v_2=v_1{\epsilon }_1+v^{\prime }\left(1-{\epsilon }_1\right)$$$$v_3=\frac{v_2}{{\epsilon }_3}$$$$p_2=p_3+\frac{\rho v_3^2}{2}-\frac{\rho v_2^2}{2}$$

绘图

下图实线是典型工况下$v^{\prime }$随$v_1$的变化曲线，由于未考虑从$p_3$到$p_1$的流动过程，故称之为内特性曲线。短虚线表示被引射气体流经环缝无压力损失条件下，根据$p_1$与$p_3$压力差直接计算得到的$v^{\prime }$，称为理想的外特性曲线。二者交点即为理想工作点。如果在此基础上考虑$p_3$到$p_1$流动过程中的压力损失，实际工作点应在理想工作点下方。

下图是$v_3$随$v_1$的变化曲线

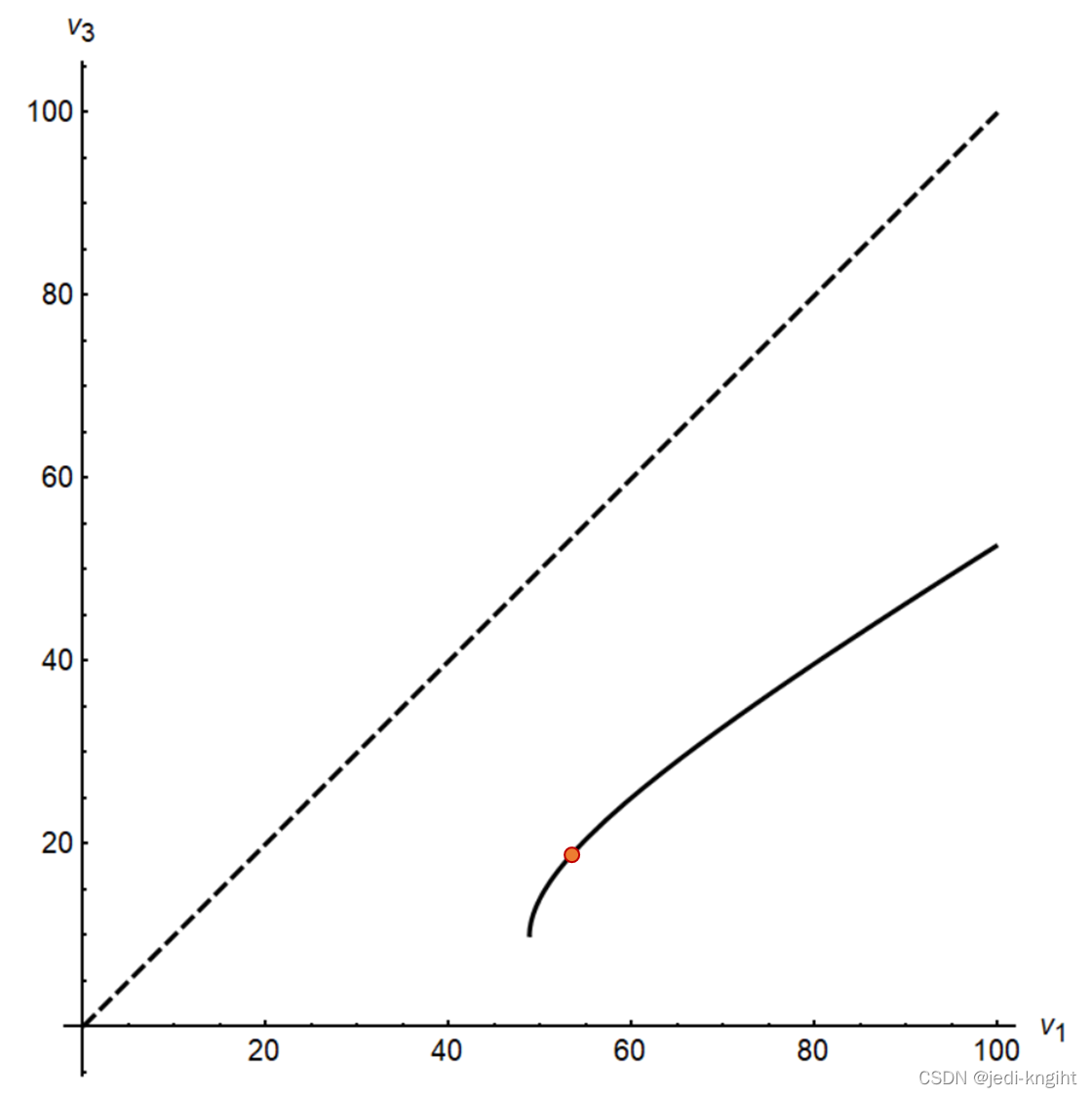
下图是$p_1-p_3$的变化曲线，当$p_1-p_3<0$时引射器才可能正常工作。